Fueling the AGN - F. Combes

2.3. Characteristic radii

First, it is obvious to define the ``accretion radius'' R_a, or the radius under which the black hole of mass M dominates the dynamics, as a function of the velocity dispersion of the stellar component around it V:

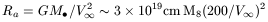
Equation 1

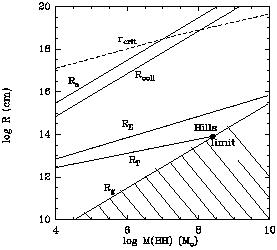
where M₈ is the black hole mass in units of 10⁸ M. The radii are plotted in figure 1 (see also Frank & Rees 1976, Luminet 1987).

Figure 1. Characteristic radii, corresponding to the various physical phenomena, as a function of black hole mass: from top to bottom, R_a, the accretion radius, R_coll, the collision radius, R_E, the Eddington radius, R_T, the tidal radius, R_g, the gravitational radius (see text for definitions). Loss-cone effects are important inside the critical radius r_crit (see section 2.4).

Then the ``collision radius'' R_coll, is the radius under which stellar collisions are disruptive, i.e. the freefall velocity around the black hole (GM/r)^1/2 is comparable to the escape speed v_* of a typical individual star (GM_*/r_*)^1/2. For solar mass stars (escape velocity of the order of 500km/s):

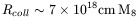
The ``Eddington radius'' is the radius under which a star receives more light than its Eddington luminosity:

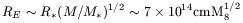
for solar mass stars. The radiation pressure can then disrupt the envelope, or at least form bloated stars, more fragile with respect to mass loss.

The ``tidal radius'' has a great importance, it is the radius under which a star is disrupted by the tidal forces of the black hole (calculated like a Roche radius):

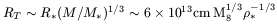
where _* is the average density of solar mass stars. From that, we can estimate the accretion rate due to tidal disruption of stars, by integrating the mass available (in _coreR_T³), divided by the dynamical time, in _core^-1/2 :

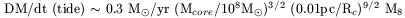
Note that the efficiency of collisions between stars becomes larger than the tidal contribution, for large compactness of the nuclear star clusters, such as their velocity dispersion _* > v_*:

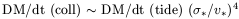
Finally, let us recall the horizon radius of the black hole (or ``gravitational radius'') under which matter cannot escape:

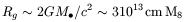
As the black hole horizon grows faster with M than the tidal radius, there is a limit, when M₈ ~ 3, above which the star disruption occurs inside the black hole, and there is no gaseous release or AGN activity (but the black hole grows even more rapidly). This is the Hills limit (Hills 1975).