


2.4. Black hole growth by star accretion
Let us compute the time required to reach the critical mass
Mc where RT = Rg, above which stars are
swallowed by the black hole without any gas radiation
(Mc = 3 108
M ).
When a tidal breakup of a star (of mass m, radius R) occurs, the
energy required is taken from the orbital energy of
the star
).
When a tidal breakup of a star (of mass m, radius R) occurs, the
energy required is taken from the orbital energy of
the star
Eb = 3/4 G m2/R
then the gas coming from the disruption will have an orbit of typical semi-major axis
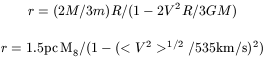
For our own Galaxy, with a 2 106
M black hole, this
means a typical radius of the gas disk of 0.03 pc.
black hole, this
means a typical radius of the gas disk of 0.03 pc.
The black hole cannot swallow the gas too fast, the maximum rate
occurs when it radiates at Eddington luminosity (above which the radiation
pressure prevents the material to fall in). This maximum
luminosity is:
LE = 3.2 104
(M / M )
L
)
L .
For a mass Mc, the maximum is 1013
L
.
For a mass Mc, the maximum is 1013
L (close to the
peak luminosity of QSOs). Then the corresponding accretion rate,
assuming an efficiency of
(close to the
peak luminosity of QSOs). Then the corresponding accretion rate,
assuming an efficiency of
 = 10-20% is
dM / dtE = 1.1 10-8 (M /
M
= 10-20% is
dM / dtE = 1.1 10-8 (M /
M )
M
)
M /yr.
This implies an exponential growth of the black hole;
it takes only 1.6 109 yr to
grow from a stellar black hole of 10
M
/yr.
This implies an exponential growth of the black hole;
it takes only 1.6 109 yr to
grow from a stellar black hole of 10
M to Mc:
to Mc:
tE= 9.3 107 ln(Mc/M) yr
Note that this very simple scheme would lead to a
maximum at z = 2.8 of the number of quasars.
This maximum rate, however, is not realistic, since
the black hole quickly gets short of fuel, as the neighbouring
stars (in particular at low angular momentum)
are depleted. Then it is necessary to consider a
growth limited by stellar density
 s :
s :
DM/dt =  s
s
 V
V
where  is the accretion
cross-section, and V the typical stellar velocity. The corresponding
time-scale to grow from M to Mc is
is the accretion
cross-section, and V the typical stellar velocity. The corresponding
time-scale to grow from M to Mc is
tD = 1.7 1015 yr
( s /
M
s /
M pc-3)-1
M / M
pc-3)-1
M / M -1/3
(1 - M / Mc1/3) <V2 >
1/2 (km/s)
-1/3
(1 - M / Mc1/3) <V2 >
1/2 (km/s)
Typically in galaxy nuclei,
 s =
107 M
s =
107 M /pc3, <V2 > 1/2
= 225 km/s.
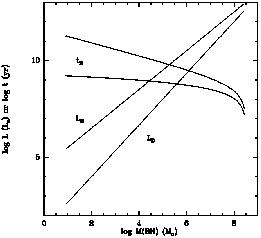
A black hole could grow up to Mc in a Hubble time, and
the luminosity at the end could be of the order of
1046 erg/s (see figure 2).
More detailed considerations
(Frank & Rees
1976,
Lightman &
Shapiro 1977)
introduce the loss-cone effect: the angular momentum can
diffuse faster than the energy (faster than a stellar relaxation time
tR).
Stars with low angular momentum, or very
excentric orbits, will be swallowed first.
Since the low angular momentum stars are replenished faster,
the loss-cone effect increases the accretion rate by:
tl = tR (1-e2),
with e the excentricity of the orbits.
This is significant inside a critical radius rcrit, where the
loss-cone angle
becomes larger than the diffusion angle
/pc3, <V2 > 1/2
= 225 km/s.
A black hole could grow up to Mc in a Hubble time, and
the luminosity at the end could be of the order of
1046 erg/s (see figure 2).
More detailed considerations
(Frank & Rees
1976,
Lightman &
Shapiro 1977)
introduce the loss-cone effect: the angular momentum can
diffuse faster than the energy (faster than a stellar relaxation time
tR).
Stars with low angular momentum, or very
excentric orbits, will be swallowed first.
Since the low angular momentum stars are replenished faster,
the loss-cone effect increases the accretion rate by:
tl = tR (1-e2),
with e the excentricity of the orbits.
This is significant inside a critical radius rcrit, where the
loss-cone angle
becomes larger than the diffusion angle
 D ~
(tdyn / tR)1/2.
This critical radius is also plotted in
figure 1.
D ~
(tdyn / tR)1/2.
This critical radius is also plotted in
figure 1.
|
Figure 2. Growth of a supermassive black hole in two simple models: accretion at Eddington luminosity (time-scale tE and corresponding luminosity LE, as a function of black hole mass MBH), and when accretion is limited by diffusion (tD and LD) (from Hills, 1975). |
More detailed considerations also can change the above scenario, for instance when a mass spectrum for the stars is taken into account. The critical mass can be then be higher than Mc, because of large mass stars: giants are less dense and disrupted before solar-mass stars. This leads to higher luminosities for the active nuclei. Also the presence of the supermassive black hole may form a cusp of stars in the center. Then the stellar density is much higher and it is Rcoll that limits the rate of accretion. Gas is produced by the star-star collisions, and again higher masses and luminosities can be reached.