3.1. Gravitational stability

The conditions of stability of a dissipation-less component like the stellar one, is relatively well known. High enough velocity dispersions are required to suppress axisymmetric instabilities and even spirals, bars or z-instabilities. The latter provide heating to the medium which becomes un-responsive. The gas is dissipative and has a completely different behaviour; it is always unstable, and its velocity dispersion is fixed by regulation and feed-back.

The local stability criterion has been established by Toomre (1964): stabilisation is obtained through pressure gradients (velocity dispersion c) at small scale, smaller than the Jeans length: = ct_ff = c² / G, where is the disk surface density. At large scale, the rotation stabilises through centrifugal forces, more precisely the scales larger than L_crit = 4² G / ² (where is the epicyclic frequency). The Safronov-Toomre criterion is obtained in equalling and L_crit:

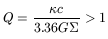
For one component, a radial mode (, k) in a linear analysis obeys the dispersion relation (where k is the wave number):

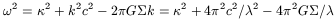
which means that self-gravity reduces the local frequency . If a stability criterium is easy to derive for one component, the same is not true for a two-components fluid, since the coupling between the two makes the ensemble more unstable than each one alone. The one-component criterion can be applied separately to the stellar and gas components, where the corresponding values of and c are used, leading to Q_s and Q_g. Because c_g << c_s however, only a small percentage of mass in gas can destabilize the whole disk, even when Q_s > 1 and Q_g > 1. For two fluids with gravitational coupling, the dispersion relation yields a criterion of neutral stability ² = 0:

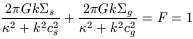
which gives directly an idea of the relative weight of gas and stars in the instabilities (cf Jog 1996). At low k (long waves), essentially the stars contribute to the instability, while at high k (short waves), the gas dominates. The neutral equilibrium requires the simultaneous solution of d² (k) / dk = 0, which leads to a system of 2 polynomial equations 4th and 3rd order in k, and no analytic criterion can be derived; there are only numerical solutions in terms of a two-fluid Q_{s - g} value, which is always lower than the Q_s or Q_g values. Q_{s - g} = 1 defines the neutral stability, by analogy with the one-fluid treatment, at the fastest growing F= 2/(1 + Q_{s - g}²). The stability depends strongly on the gas mass fraction (between 5 and 25%), and there can be sharp transitions from high to low values of , as the mass fraction increases from = 0.1 to 0.15 for instance. When Q_s is high and Q_g is low (a frequent situation, given the dissipation and cooling in the gas), the main instability is at small-scales. A gas-rich galaxy (with > 0.25) is only stable at very low surface densities (this explains the Malin 1-type galaxies, Impey & Bothun 1989); the center of early-type galaxies, where Q_s is high, and Q_g is low (due to low gas velocity dispersion), could be dominated by the gas wavelength, even at very low gas mass fraction: this can explain spiral arms in galaxies such as NGC 2841 (Block et al 1996). Also interaction of galaxies, by bringing in a high amount of gas, may change abruptly the fastest growing wavelength from _s to _g , and trigger star-formation. Even beyond the neutral stability criterium, when Q_{s - g} > 1, a galaxy disk can be unstable with respect to non-axisymmetric perturbations, such as bars or spirals; in this case also, the two-fluid coupling increases the instability, i.e. the disk will form a bar, even if the stars or the gas alone are stable with respect to such perturbations (Jog 1992).