


3.2. Feedback on the dynamics
Many photometric and kinematic studies have computed the Q values over galactic disks, and it appears that Q does not follow big variations, but on the contrary is almost constant over the systems, as if self-regulating processes were at work. The stellar dispersion has been studied in our own galaxy and in a few external galaxies by Lewis & Freeman (1989) and Bottema (1993). The velocity dispersion decreases exponentially with radius, in parallel to the stellar surface density, and Qs is nearly constant as a function of radius, at least for large galaxies, and vary between 2 and 3 from galaxy to galaxy.
If the stellar disk can be considered as a self-gravitating infinite slab,
locally isothermal
( z independent of
z), its density obeys:
z independent of
z), its density obeys:
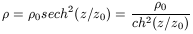
where z0 is the characteristic scale-height of the stellar disk, given by
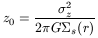
where  z is the
vertical velocity dispersion, and
z is the
vertical velocity dispersion, and
 s(r) =
z0
s(r) =
z0
 0 is the
surface density.
The latter has a general exponential behaviour
(e.g. Freeman 1970),
with a radial scale-length h. The scale-height
z0 has been
observed to be independent of radius
(van der Kruit &
Searle 1981,
1982,
de Grijs et al 1997),
and there are only small departures from isothermality in z
(van der Kruit 1988).
Then, if the mass to light ratio is constant with radius for
the whole stellar disk, and there is no or little dark matter within the
optical disk, we expect to find a velocity dispersion varying as
e-r/2h. This is exactly what is found, within the
large uncertainties
(Bottema 1993).
Since some galaxies of the sample are edge-on and
others face-on, the comparison requires to know the relation between z
and r projection of the dispersion. In the solar neighbourhood,
0 is the
surface density.
The latter has a general exponential behaviour
(e.g. Freeman 1970),
with a radial scale-length h. The scale-height
z0 has been
observed to be independent of radius
(van der Kruit &
Searle 1981,
1982,
de Grijs et al 1997),
and there are only small departures from isothermality in z
(van der Kruit 1988).
Then, if the mass to light ratio is constant with radius for
the whole stellar disk, and there is no or little dark matter within the
optical disk, we expect to find a velocity dispersion varying as
e-r/2h. This is exactly what is found, within the
large uncertainties
(Bottema 1993).
Since some galaxies of the sample are edge-on and
others face-on, the comparison requires to know the relation between z
and r projection of the dispersion. In the solar neighbourhood,
 z =
0.6
z =
0.6 r, and this ratio
is assumed to be valid in external galaxies too.
r, and this ratio
is assumed to be valid in external galaxies too.
As for the gaseous component, the vertical velocity dispersion
is constant with radius in the outer parts of galaxies, where the rotation
curve is flat
(Dickey et al 1990,
Combes &
Becquaert 1997):
cg  6km/s. The behaviour of
6km/s. The behaviour of

 1/r (for a flat
rotation curve) is
exactly parallel to the gas surface density
1/r (for a flat
rotation curve) is
exactly parallel to the gas surface density
 g
g
 1/r (e.g.
Bosma 1981),
and therefore Qg
1/r (e.g.
Bosma 1981),
and therefore Qg
 cg
cg /
/
 g is constant with
radius in the outer parts. This strongly suggests a regulation mechanism,
that could maintain the values of Q about constant for both stars and
gas.
g is constant with
radius in the outer parts. This strongly suggests a regulation mechanism,
that could maintain the values of Q about constant for both stars and
gas.
The mechanism could be simply gravitational instabilities coupled with gas dissipation. When the medium is cool enough, so that the Q value is too low, gravitational instabilities quickly provide heating. The stellar component cannot cool down and keeps hot, although this is somewhat moderated by the gravitational action of the gas, and the young stars born in the cool component. The gas is even more sensitive to the heating, but it can dissipate its disordered motions. The key point is that cooling encourages dynamical instabilities, and therefore produces heating, which is how the regulation works (cf Bertin & Romeo 1988).
It is tempting to relate the gas stability criterium (Qg ~ 1) to the threshold for star formation in galaxy disks (cf Kennicutt, 1989). However, things are certainly less simple, since the gas component does not form stars as soon as it is unstable and form clouds. In the outer parts of galaxies, the HI gas that extends much further than the last radius of star-formation, appears patchy, clumpy, and following some kind of spiral structure. The outer gas is unstable at any scale. This suggests that instabilities are present, at the origin of cloud formation, and are the regulator of the constant cg and Qg (Lin & Pringle 1987).
Note that there are several ways to maintain Q constant, and that the stars and gas have chosen two different ways: the stellar component keeps its scale-height constant, while its velocity dispersion is exponentially decreasing with radius; the gas keeps its velocity dispersion constant, while its scale-height increases steadily with radius (linearly, when the rotation curve is flat). This might be related to the different radial distribution. The gas does not display an exponential radial profile, may be due to continued infall or accretion.