Annu. Rev. Astron. Astrophys. 1992. 30: 575-611 Copyright © 1992 by Annual Reviews. All rights reserved

5. THE FIR/RADIO CORRELATION

A correlation between the 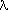= 10 µm mid-infrared and 1415 MHz radio luminosities of Seyfert galaxy nuclei was discovered by van der Kruit (1971) and soon extended to the nuclei of normal spiral galaxies (van der Kruit 1973). At first both the infrared and radio emission were thought to be synchrotron radiation from relativistic electrons accelerated by nuclear monsters (e.g. massive black holes in Seyfert galaxies or other AGNs). Then Harwit & Pacini (1975) proposed that the infrared is thermal reradiation from dusty H II regions, while the 1415 MHz luminosity is dominated by synchrotron radiation from relativistic electrons accelerated in SNRs from the same population of massive stars that heat and ionize the H II regions. Condon et al. (1982) classified the luminous central sources in spiral galaxies as either starbursts or monsters by their radio sizes and morphologies, and they suggested that the infrared/radio ratio could be used to distinguish starbursts from monsters since the correlation was much tighter for nuclear starbursts than for monsters. Rickard & Harvey (1984) found that the FIR/radio correlation applies to the disks of normal galaxies as well.

The real significance of the FIR/radio correlation for normal galaxies ­ that it is so tight and so universal ­ was not appreciated until the large IRAS survey appeared. The IRAS flux densities at 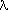= 60 µm and 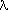= 100 µm can be used to calculate the quantity FIR

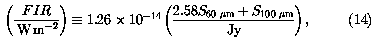
which is the total flux between 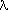~ 40 µm and 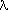~ 120 µm. FIR measures the majority of the flux reradiated by dust in normal galaxies (Helou et al. 1988). Helou et al. (1985) defined the parameter

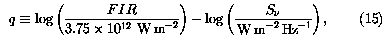
where ~ 1.4 GHz unless otherwise specified, as a logarithmic measure of the FIR/radio flux-density ratio. The distribution of q was found to be quite narrow (rms scatter _q 0.2 about the median < q > ~ 2.3 at = 1.4 GHz) among spiral galaxies in Virgo (Helou et al. 1985), a large, inhomogeneous sample of spiral and irregular galaxies (Wunderlich et al. 1987), Sbc galaxies (Hummel et al. 1988a), E/S0 galaxies with current star formation (Dressel 1988, Wrobel & Heeschen 1988, 1991), extragalactic FIR sources selected at 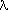= 60 µm (Condon & Broderick 1986, 1991), and radio flux-limited samples of normal galaxies (Condon & Broderick 1988, Condon et al. 1991b). The FIR/radio correlation (Condon et al. 1991a) for galaxies in the revised IRAS BGS (Soifer et al. 1989) is plotted in Figure 8.

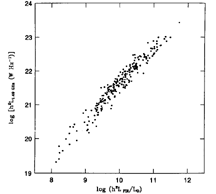Figure 8 The FIR/radio correlation for strong sources selected at = 60 µm and not containing known monsters (e.g. Seyfert nuclei) or optically thick to free-free absorption at = 1.49 GHz. The measurement errors are smaller than the intrinsic scatter for this sample. Abscissa: log FIR luminosity in solar units. Ordinate: log 1.49 GHz luminosity (W Hz^-1).

Since synchrotron emissivity (power radiated per unit volume) is proportional to B^{( + 1)/2} = B^{(1 + )} for a given density N₀E^- of relativistic electrons (Equation 10), it was proposed (Hummel 1986, Hummel et al. 1988a) that deviations of individual galaxies from the average FIR/radio ratio reflect variations in B^{(1 + )}. The FIR/radio ratio is now known to be nearly constant over a range of ~ 10⁴ in U_m 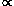B² ~ B^{(1 + )} (Condon et al. 1991c), where U_m is again the magnetic energy density, so this does not seem to be the case. If the cosmic-ray production rate is proportional to L_FIR, the FIR/radio correlation actually requires that the total radio energy emitted per relativistic electron during its lifetime be nearly independent of U_m but it does not constrain the instantaneous radio power emitted by each electron. Apparently, galaxies conspire to fix the ratio of synchrotron energy losses to the radio-quiet losses from inverse-Compton scattering, bremsstrahlung, ionization, adiabatic expansion, and escape into intergalactic space.

Several explanations for this conspiracy have been proposed. Völk (1989) argued that the break frequencies (Equation 12) of normal galaxies are _b 5 GHz; that is, galaxies are ``calorimeters'' or ``beam dumps'' in which relativistic electrons lose most of their energy to synchrotron and inverse-Compton radiation. The ratio of synchrotron to total energy loss is therefore ~ U_m / (U_m + U_r), where U_r is the radiation energy density, which must be nearly constant to save the FIR/radio correlation. Stars are the dominant source for the radiation energy density U_r in most normal galaxies at low redshifts, although the independent contribution to U_r from the cosmic microwave background grows as (1 + z)⁴ and might quench the radio emission at redshifts z 1. Turbulence associated with star formation could amplify the magnetic energy density (Ko & Parker 1989) until it is comparable with the interstellar turbulent pressure P_e = 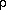< v² > / 3, where the rms turbulent velocity < v² >^1/2 is about 10 km s^-1 in our galaxy. This mechanism will tend to keep the ratio U_m / (U_m + U_r) constant if the star-formation rate varies. However, it may be difficult to reconcile both the FIR/radio correlation (which requires that the radio energy density be roughly proportional to U_r) and a constant U_m / (U_m + U_r) with minimum energy or equipartition magnetic fields since the relation between the minimum-energy magnetic energy density U_min and radio energy density U_radio is not linear: U_min 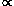U_radio^4/7 (Equation 13). Also, the FIR/radio correlation holds at frequencies as low as 0.151 GHz (Cox et al. 1988), and the observed nonthermal spectral indices of normal galaxies well below 5 GHz are not as steep as might be expected: If 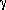₀ 2 (Bell 1978) then 1 for _b. Chi & Wolfendale (1990) investigated models in which relativistic electrons diffuse out of all but the most luminous galaxies to get nonthermal spectral indices in better agreement with the observations. They assumed U_m ~ U_r so U_m / (U_m + U_m) ~ 1/2 automatically. Their assumed diffusion coefficient is proportional to U_m so that cosmic rays escape more quickly from galaxies with strong magnetic fields, although Lerche & Schlickeiser (1980) have argued that the diffusion coefficient D should decrease with B. Finally, the radio emitting volume was claimed to be proportional to L_FIR^{0.9 ± 0.4}. Thus, the emissivity is nearly independent of luminosity, in contrast with the observation that sources with higher L_FIR have smaller volumes and very high emissivities (Condon et al. 1990). These assumptions are so strong that they leave little room for departures from the FIR/radio correlation, but they may not be valid for real galaxies.

The observed FIR/radio correlation is not precisely linear, especially in optically selected samples containing very low-luminosity galaxies (Fitt et al. 1988, Cox et al. 1988, Devereux & Eales 1989). Galaxies with low FIR luminosities have even lower radio luminosities than expected. Such a nonlinearity would occur if either the FIR or radio luminosity is not directly proportional to the star-formation rate. The two-component model for FIR emission (Helou 1986, Lonsdale-Persson & Helou 1987) includes a warm ``active'' component from dusty molecular clouds heated by the massive young stars responsible for radio emission plus a cool ``cirrus'' component of dust heated by the general interstellar radiation field. If the cirrus component of galaxies in a quiescent phase is heated primarily by the older, radio-quiet stellar population, the cirrus contribution to L_FIR should be subtracted to make the FIR/radio correlation linear. Fitt et al. (1988) attempted to correct the FIR/radio correlation by using the observed FIR color temperature to estimate and subtract the FIR emission from the cool (they assumed T ~ 20 K) dust component of each galaxy. Devereux & Eales (1989) argued that the intensity of the radiation field heating the cirrus component is proportional to the blue luminosity, and they subtracted a fixed fraction of the blue luminosity from the FIR luminosity of each galaxy to linearize the FIR/radio correlation.

Alternatively, Chi & Wolfendale (1990) assumed that the FIR luminosity is proportional to the current rate of massive star formation and hence cosmic-ray production, but that the radio luminosity might be deficient in low-luminosity galaxies because the cosmic rays are more likely to escape by diffusion (or convection). They corrected the observed radio luminosities for their estimate of these losses to make the FIR/radio correlation linear. Condon et al. (1991a) investigated the FIR/radio correlation for two well-defined samples of normal galaxies ­ optically selected spiral galaxies brighter than B_T = +12 and the IRAS Revised Bright Galaxy Sample with S_{60 µm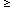} 5.24 Jy ­ with sufficiently accurate 1.49 GHz flux densities for individual measurement errors in q to be smaller than the intrinsic scatter in the q distribution. They found that none of the corrections described above can simultaneously linearize the FIR/radio correlation and reduce the observed scatter for both galaxy samples. An empirical correction to q was found that depends on the blue/radio ratio; it can simultaneously linearize the correlation and reduce the scatter. The galaxies needing the largest corrections generally have the lowest radio and infrared luminosities but normal blue luminosities, suggesting that their current star-formation rates may be lower than the average over the last ~ 10⁹ yr. Thus, the empirical correction is consistent with Helou's (1986) two-component model, but only if the radio-loud population of massive (M 8 M) stars heats both the warm dust in H II regions and contributes significantly to heating the cirrus dust, which need not be very cool. Xu (1990) has recently argued that the cirrus is heated by nonionizing UV from short-lived stars in the 5-20 M range. Devereux & Young (1990) used the F(H)/FIR ratio to suggest that the dust contributing to FIR is heated primarily by stars with M 6 M, at least in galaxies with L_FIR > 10⁹ L. Both L_FIR and the production rate of cosmic rays thus appear to be directly proportional to the recent formation rate of massive stars in most normal galaxies. However, this is not sufficient to ensure a tight FIR/radio correlation; it is still necessary to show that the nonthermal radio energy produced per relativistic electron does not vary significantly from galaxy to galaxy. Indeed, cosmic-ray escape or other losses may be a factor in the high FIR/radio ratios of low-luminosity (L_FIR < 10⁹ L) galaxies, especially dwarf galaxies with relatively flat radio spectra (Klein et al. 1984).