Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
575-611 Copyright © 1992 by Annual Reviews. All rights reserved |
The lifetimes of the massive stars responsible for most of the radio emission
from normal galaxies are much shorter than a Hubble time, so the current
radio luminosity is proportional to the recent star-formation
rate. Biermann (1976) first
included thermal and nonthermal radio flux
measurements in quantitative galaxy models because they had ``attained a
precision which is comparable to or in some cases clearly better than
the precision of optical measurements.'' This pioneering work compared
(B - V) colors with blue/radio flux ratios. Biermann assumed a
time-independent power-law IMF 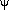 (M)
(M) 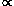 M-
M-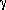 , with slope
, with slope 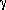 = 2.35 and upper
mass limit MU. All stars with M
= 2.35 and upper
mass limit MU. All stars with M 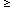 MSN ~ 6.7
M
MSN ~ 6.7
M were presumed to produce
radio-emitting supernova remnants, so the radio supernova rate is
were presumed to produce
radio-emitting supernova remnants, so the radio supernova rate is
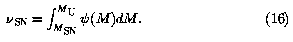
His flux-time integral for each supernova remnant – 0.1 Jy yr at
 = 5 GHz when seen from a distance d =
20 Mpc – is an extrapolation of the observed (Clark & Caswell 1976)
surface brightness-diameter (
= 5 GHz when seen from a distance d =
20 Mpc – is an extrapolation of the observed (Clark & Caswell 1976)
surface brightness-diameter (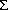 - D)
relation for Galactic supernova remnants. Biermann noted that the lower
mass limit MSN for radio supernovae is more critical
than MU
- D)
relation for Galactic supernova remnants. Biermann noted that the lower
mass limit MSN for radio supernovae is more critical
than MU ![]() MSN because the steep IMF slope implies that most
radio supernova progenitors have masses just above
MSN. The resulting models could be made to agree with
the observed blue/radio ratios only if the assumed
nonthermal radio energy per supernova were increased by a factor of ten.
MSN because the steep IMF slope implies that most
radio supernova progenitors have masses just above
MSN. The resulting models could be made to agree with
the observed blue/radio ratios only if the assumed
nonthermal radio energy per supernova were increased by a factor of ten.
A very clear derivation of the relation between the supernova rate
and the nonthermal radio luminosity implied by the 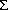 - D relation was given by Ulvestad (1982). The 408 MHz
data indicate
- D relation was given by Ulvestad (1982). The 408 MHz
data indicate 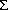 (W m-2
Hz-1 sr-1) ~ 10-15
[D(pc)]-3 and D(pc) ~ 0.43
E501/5[n(cm-3)]-1/5[t(yr)]2/5,
where E50 is the explosion energy in units of
1050 ergs, n is the ambient particle density, and
t is the time since the supernova explosion (Clark & Caswell
1976). If the supernova remnant is a radio source only during its
adiabatic lifetime
(W m-2
Hz-1 sr-1) ~ 10-15
[D(pc)]-3 and D(pc) ~ 0.43
E501/5[n(cm-3)]-1/5[t(yr)]2/5,
where E50 is the explosion energy in units of
1050 ergs, n is the ambient particle density, and
t is the time since the supernova explosion (Clark & Caswell
1976). If the supernova remnant is a radio source only during its
adiabatic lifetime  (yr) ~ 2 x 104
E504/17
[n(cm-3)]-9/17, then
(yr) ~ 2 x 104
E504/17
[n(cm-3)]-9/17, then
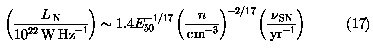
at 408 MHz. Ulvestad (1982) used
a relation similar to Equation 17 to
derive  SN from the observed radio
luminosities of Seyfert galaxies. He
scaled the infrared/optical luminosities from the classic Rieke et al. (1980)
model D for M82 with
SN from the observed radio
luminosities of Seyfert galaxies. He
scaled the infrared/optical luminosities from the classic Rieke et al. (1980)
model D for M82 with  SN and found
them to exceed the observed values
by at least a factor of ten. This prompted his suggestion that the radio
sources in most Seyfert galaxies are powered by AGNs instead of stars.
SN and found
them to exceed the observed values
by at least a factor of ten. This prompted his suggestion that the radio
sources in most Seyfert galaxies are powered by AGNs instead of stars.
Gehrz et al. (1983) constructed a
steady-state model for the compact
starbursts in NGC 3690 that unified features of the earlier models, and
they used the FIR luminosity as the best estimate of the bolometric
luminosity of a starburst. Gehrz et
al. (1983) compared H , FIR,
and radio continuum luminosities of NGC 3690 with starburst models
parameterized by different IMF slopes
, FIR,
and radio continuum luminosities of NGC 3690 with starburst models
parameterized by different IMF slopes 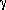 and
mass limits ML, MU. They also found
it difficult to reconcile the high supernova
rate needed to explain the nonthermal radio emission with the observed
FIR and H
and
mass limits ML, MU. They also found
it difficult to reconcile the high supernova
rate needed to explain the nonthermal radio emission with the observed
FIR and H luminosities. Their successful
models have a very steep (
luminosities. Their successful
models have a very steep (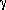 = 3.5) and
severely truncated (MU ~ 25 M
= 3.5) and
severely truncated (MU ~ 25 M ) IMF, plus a low MSN ~ 6
M
) IMF, plus a low MSN ~ 6
M . Such
models favor
. Such
models favor  SN while minimizing the
bolometric luminosity and Nuv. They cannot be applied
to all galaxies since the discovery of Wolf-Rayet stars in some FIR
luminous galaxies (Armus et
al. 1988) proves that the IMF does extend
beyond 25 M
SN while minimizing the
bolometric luminosity and Nuv. They cannot be applied
to all galaxies since the discovery of Wolf-Rayet stars in some FIR
luminous galaxies (Armus et
al. 1988) proves that the IMF does extend
beyond 25 M in galaxies obeying the ubiquitous FIR/radio correlation.
in galaxies obeying the ubiquitous FIR/radio correlation.
These and related difficulties are unavoidable if the SNRs themselves
are required to provide all of the nonthermal radio emission from normal
galaxies. Heckman et al. (1983)
argued that monsters in AGNs, not
starbursts, power strong nuclear sources in spiral galaxies since the
average radio spectral index <  > ~ 0.45 of
Galactic SNRs is significantly less than the average spectral index
<
> ~ 0.45 of
Galactic SNRs is significantly less than the average spectral index
<  > ~ 0.75 of spiral galaxies. Jenkins (1984)
could not reconcile the high supernova rate required to explain the
nonthermal radio luminosity of the normal spiral galaxy NGC 5953 with
its H
> ~ 0.75 of spiral galaxies. Jenkins (1984)
could not reconcile the high supernova rate required to explain the
nonthermal radio luminosity of the normal spiral galaxy NGC 5953 with
its H and bolometric luminosities,
concluding that ``no explanation can be found for the radio emission.''
Kronberg & Biermann (1981) found
excessive consumption of H I mass by
the starburst nucleus of NGC 2146. For the LN ~ 6 x
1021 W Hz-1
nonthermal luminosity of our galaxy at 408 MHz (Berkhuijsen 1984),
Equation 17 implies an excessive radio supernova rate
and bolometric luminosities,
concluding that ``no explanation can be found for the radio emission.''
Kronberg & Biermann (1981) found
excessive consumption of H I mass by
the starburst nucleus of NGC 2146. For the LN ~ 6 x
1021 W Hz-1
nonthermal luminosity of our galaxy at 408 MHz (Berkhuijsen 1984),
Equation 17 implies an excessive radio supernova rate  SN ~ 0.4 yr-1. This is much higher than the
Type II supernova rate
SN ~ 0.4 yr-1. This is much higher than the
Type II supernova rate  SN ~ 0.023
yr-1 estimated by Tammann
(1982) or the
Galactic pulsar birthrate 0.01-0.03 yr-1 (Lyne et al. 1985). Even
the radio counts of young Galactic SNRs suggest a radio supernova rate
SN ~ 0.023
yr-1 estimated by Tammann
(1982) or the
Galactic pulsar birthrate 0.01-0.03 yr-1 (Lyne et al. 1985). Even
the radio counts of young Galactic SNRs suggest a radio supernova rate
 SN ~ 0.013 yr-1 (Caswell & Lerche 1979), albeit with
large uncertainty (Green 1984). Supernova
remnants may accelerate the relativistic electrons producing the
nonthermal radio emission in spiral galaxies, but > 90% of this emission
must be produced long after the individual supernova remnants have faded
out and the electrons have diffused throughout the galaxy – an old
(Pooley 1969, Ilovaisky & Lequeux 1972) but often
overlooked result. Therefore, Condon
& Yin (1990) dropped Equation 17 in favor of
the observed Galactic relation between LN and
SN ~ 0.013 yr-1 (Caswell & Lerche 1979), albeit with
large uncertainty (Green 1984). Supernova
remnants may accelerate the relativistic electrons producing the
nonthermal radio emission in spiral galaxies, but > 90% of this emission
must be produced long after the individual supernova remnants have faded
out and the electrons have diffused throughout the galaxy – an old
(Pooley 1969, Ilovaisky & Lequeux 1972) but often
overlooked result. Therefore, Condon
& Yin (1990) dropped Equation 17 in favor of
the observed Galactic relation between LN and  SN, which implies
SN, which implies
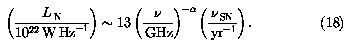
Equation 18 probably applies to most normal galaxies, since significant
variations in the ratio LN /  SN from galaxy to galaxy would
violate the observed FIR/radio correlation. Also, Völk et
al. (1989) have argued that the cosmic-ray energy production per
supernova is the same in the starburst galaxy M82 as in our galaxy.
SN from galaxy to galaxy would
violate the observed FIR/radio correlation. Also, Völk et
al. (1989) have argued that the cosmic-ray energy production per
supernova is the same in the starburst galaxy M82 as in our galaxy.