Copyright © 1992 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1992. 30:
575-611 Copyright © 1992 by Annual Reviews. All rights reserved |
The global radio nonthermal and thermal luminosities plus the FIR/radio
ratio for most normal galaxies can be approximated by a simple model
with only one free parameter, the average formation rate of stars more
massive than 5 M :
:

The ``extended'' Miller-Scalo
(1979) IMF 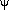 (M)
(M) 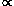 M-5/2 is
truncated at MU ~ 100 M
M-5/2 is
truncated at MU ~ 100 M . All stars more massive than
MSN = 8 M
. All stars more massive than
MSN = 8 M become radio supernovae, so the radio supernova rate
become radio supernovae, so the radio supernova rate
 SN is determined directly by the
star-formation rate:
SN is determined directly by the
star-formation rate:
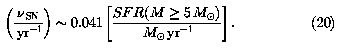
The nonthermal luminosity LN can then be obtained from Equation 18; it is
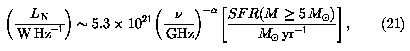
where  ~ 0.8 is the nonthermal spectral index.
~ 0.8 is the nonthermal spectral index.
The radio thermal fraction can be estimated from stellar models for an assumed electron temperature Te ~ 104 K if dust absorption of Lyman continuum photons is negligible. The results of Kennicutt (1983a) imply
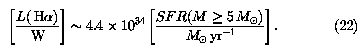
Then Equations 2, 3, and 4 yield
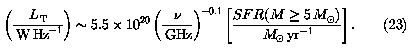
The thermal fraction implied by the ratio of Equations 21 and 23 agrees well with the average observed value (Equation 5). The ionization rate is
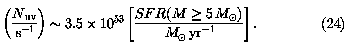
Blue luminosity is a poor quantitative measure of very recent (<
108 yr) star formation because of extinction in molecular clouds
plus confusion by older (up to 109 yr) unobscured stellar
populations of blue stars (Sage &
Solomon 1989). Massive stars are
formed in dusty giant molecular clouds from which only a small fraction
of the UV or even optical (e.g. H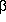 ) photons actually escape, so
that nearly all of the luminosity produced by stars in H II regions
emerges in the FIR. For typical dust temperatures and emissivities,
about 2/3 of this emission appears in the FIR band between
) photons actually escape, so
that nearly all of the luminosity produced by stars in H II regions
emerges in the FIR. For typical dust temperatures and emissivities,
about 2/3 of this emission appears in the FIR band between 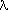 ~ 40 µm and
~ 40 µm and 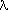 ~ 120 µm (Helou et al. 1988). Conversely, most
of the luminosity in the band measured by FIR
is from dust heated by stars more massive than M ~ 5
M
~ 120 µm (Helou et al. 1988). Conversely, most
of the luminosity in the band measured by FIR
is from dust heated by stars more massive than M ~ 5
M (Devereux & Young 1990, Xu 1990). For a time-independent IMF
(Devereux & Young 1990, Xu 1990). For a time-independent IMF
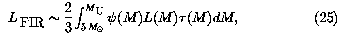
where  (M) is the lifetime of a star
with mass M and L(M) is its average bolometric
luminosity. The total energy L(M)
(M) is the lifetime of a star
with mass M and L(M) is its average bolometric
luminosity. The total energy L(M) (M) emitted by a massive star during its main-sequence
life (Maeder 1987) can be
approximated by L
(M) emitted by a massive star during its main-sequence
life (Maeder 1987) can be
approximated by L ~ 109.6 (M / M
~ 109.6 (M / M )3/2 L
)3/2 L yr. If the IMF slope is
yr. If the IMF slope is 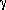 ~ 2.5
for M
~ 2.5
for M ![]() 5
M
5
M ,
then each logarithmic stellar mass range contributes equally to
LFIR and
,
then each logarithmic stellar mass range contributes equally to
LFIR and
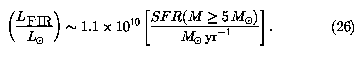
Both LN + LT and
LFIR are proportional to the star-formation
rate, so this model implies a linear FIR/radio correlation. The
FIR/radio ratio at  ~ 1.4 GHz predicted by
Equations 21, 23, and 26 is q ~ 2.4, close to the average
observed value < q > ~ 2.3 for moderately luminous
(LFIR
~ 1.4 GHz predicted by
Equations 21, 23, and 26 is q ~ 2.4, close to the average
observed value < q > ~ 2.3 for moderately luminous
(LFIR ![]() 109 L
109 L )
galaxies (Condon et
al. 1991a). Also, the ratio L(H
)
galaxies (Condon et
al. 1991a). Also, the ratio L(H ) / LFIR ~ 0.01
from Equations 22 and 26 is in reasonable agreement with the data in
Devereux & Young (1990).
) / LFIR ~ 0.01
from Equations 22 and 26 is in reasonable agreement with the data in
Devereux & Young (1990).
Since SRF(M 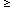 5 M
5 M ) is the only free parameter, only one observable
(e.g. the radio luminosity at one frequency) per galaxy is needed to
determine its model parameters. For example, the measured radio luminosity of
M82 is LN + LT ~ 1.0 x
1022 W Hz-1 at
) is the only free parameter, only one observable
(e.g. the radio luminosity at one frequency) per galaxy is needed to
determine its model parameters. For example, the measured radio luminosity of
M82 is LN + LT ~ 1.0 x
1022 W Hz-1 at  = 1.4
GHz. The ratio LN / LT ~ 8
follows from either Equation 5 or the ratio of Equations 21 and 23. The
model then predicts the star-formation rate SFR(M
= 1.4
GHz. The ratio LN / LT ~ 8
follows from either Equation 5 or the ratio of Equations 21 and 23. The
model then predicts the star-formation rate SFR(M 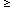 5 M
5 M )
~ 2.2 M
)
~ 2.2 M yr-1,
the radio supernova rate
yr-1,
the radio supernova rate  SN ~ 0.1
yr-1, the ionization rate Nuv ~ 8 x
1053 s-1, and the FIR luminosity
LFIR ~ 2.4 x 1010 L
SN ~ 0.1
yr-1, the ionization rate Nuv ~ 8 x
1053 s-1, and the FIR luminosity
LFIR ~ 2.4 x 1010 L . These values are all in very good
agreement with the data.
. These values are all in very good
agreement with the data.
The relative contributions to  SN
SN
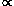 LN,
LFIR, and Nuv
LN,
LFIR, and Nuv 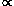 LT from stars in different ranges of
log(M / M
LT from stars in different ranges of
log(M / M )
are plotted for this model in Figure 9. Since
the range of stellar
masses contributing most to
)
are plotted for this model in Figure 9. Since
the range of stellar
masses contributing most to  SN falls
within the broad range of masses producing LFIR, the
FIR/radio ratio should be relatively insensitive to time variability or
slope changes in the assumed IMF. The thermal fraction
LT / (LN + LT) is
less robust because there is less overlap between the stellar mass
ranges responsible for supernovae and ionization. The steady-state
models of Leitherer (1990)
indicate that a change
SN falls
within the broad range of masses producing LFIR, the
FIR/radio ratio should be relatively insensitive to time variability or
slope changes in the assumed IMF. The thermal fraction
LT / (LN + LT) is
less robust because there is less overlap between the stellar mass
ranges responsible for supernovae and ionization. The steady-state
models of Leitherer (1990)
indicate that a change 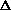
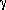 in the IMF slope changes the log
of the thermal fraction by approximately -
in the IMF slope changes the log
of the thermal fraction by approximately - 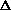
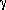 / 2. About 3 x 106 yr after
the termination of a starburst, the ionization rate (Leitherer 1990) and
hence the thermal luminosity fall precipitously while the supernova rate
and nonthermal emission persist. Thus, it is unlikely that the sharp
spectral cutoff at
/ 2. About 3 x 106 yr after
the termination of a starburst, the ionization rate (Leitherer 1990) and
hence the thermal luminosity fall precipitously while the supernova rate
and nonthermal emission persist. Thus, it is unlikely that the sharp
spectral cutoff at  ~ 8 GHz reported for
NGC 1569 is a consequence of relativistic electron energy losses in a
post-starburst galaxy (Israel & de
Bruyn 1988) since NGC 1569 still has
a normal thermal fraction.
~ 8 GHz reported for
NGC 1569 is a consequence of relativistic electron energy losses in a
post-starburst galaxy (Israel & de
Bruyn 1988) since NGC 1569 still has
a normal thermal fraction.
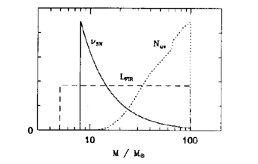 Figure 9. The relative contributions to
the supernova rate
Figure 9. The relative contributions to
the supernova rate  SN, the
far-infrared luminosity LFIR, and the ionization rate
Nuv (the last from Leitherer 1990) per logarithmic
interval of stellar mass for a time-independent IMF
SN, the
far-infrared luminosity LFIR, and the ionization rate
Nuv (the last from Leitherer 1990) per logarithmic
interval of stellar mass for a time-independent IMF 
 M-5/2
truncated at MU = 100 M
M-5/2
truncated at MU = 100 M . Abscissa: log stellar mass in solar
mass units. Ordinate: relative contribution per logarithmic mass range.
. Abscissa: log stellar mass in solar
mass units. Ordinate: relative contribution per logarithmic mass range.