Annu. Rev. Astron. Astrophys. 1994. 32: 371-418 Copyright © 1994 by Annual Reviews. All rights reserved

8. THE VALUE OF

Assuming that the inferred motions are real and generated by GI, they can be used to estimate . Evidence from virialized systems on smaller scales suggest a low-density universe of ~ 0.1-0.2, but these values may be biased. The spatial variations of the large-scale velocity field now allow measuring the mass density in a volume closer to a ``fair'' sample. One family of methods is based on comparing the dynamical fields derived from velocities to the fields derived from galaxy redshifts (Section 8.1, 8.2). These methods can be applied in the linear regime but they always rely on the assumed biasing relation between galaxies and mass often parametrized by b, so they provide an estimate of f() / b. Another family of methods measures from redshift surveys alone, based on z-space deviations from isotropy (Section 8.3). Finally, there are methods which rely on non-linear effects in the velocity data alone, and provide estimates of independent of b (Section 8.4, 8.5). The various estimates of and are summarized in Table 1 at the end of the section. Note that the errors quoted by different authors reflect different degrees of sophistication in the error analysis, and are in many cases underestimates of the true uncertainty.

8.1 from Galaxies versus the CMB Dipole

Equation (19) is best at estimating v(0), the linear velocity of the LG in the CMB frame due to the gravitational acceleration g(0) exerted by the mass fluctuations around it. A comparison with the LG velocity of 627 ± 22 km s^-1 as given by the CMB dipole is a direct measure of . One expects to obtain a lower bound on because v ~ 600 km s^-1 is very improbable in a low-density universe. One way to estimate g(0) is from a whole-sky galaxy survey where only the angular positions and the fluxes (or diameters) are observed, exploiting the coincidence of nature that both the apparent flux and the gravitational force vary as r^-2. If L M, then the vector sum of the fluxes in a volume-limited sample is g(0) due to the mass in that volume. This idea can be modified to deal with a flux-limited sample once the luminosity function is known, and applications to the combined UGC/ESO diameter-limited catalog of optical galaxies yield _opt values in the range 0.3-0.5 (Lahav 1987; Lynden-Bell et al. 1989). These estimates suffer from limited sky coverage, uncertain corrections for Galactic extinction, and different selection procedures defining the north and south samples. The IRAS catalog provides a superior sky coverage of 96% of the sky, with negligible Galactic extinction and with fluxes observed by one telescope, but with possible under-sampling of cluster cores (Kaiser & Lahav 1989). A typical estimate from the angular IRAS catalog is _I = 0.9 ± 0.2 (Yahil et al. 1986).

The redshift surveys provide the third dimension which could help in deriving g(0) by Equation (19), subject to the difficulties associated with discrete, flux-limited sampling (Section 5). The question is whether g(0) is indeed predominantly due to the mass within the volume sampled, i.e., whether g(0) as computed from successive concentric spheres converges interior to R_max. This is an issue of fundamental uncertainty (e.g. Lahav et al. 1990; Juszkiewicz et al. 1990; Strauss et al. 1992b). The r - z mapping (21) could either compress or rarify the z-space volume elements depending on the sign of u in the sense that an outflow makes the z-space density _z smaller than the true density : _z(x) (x) - 2[v(x) - v(0)] · rhat / r. The varying selection function adds to this geometrical effect [in analogy to n (r) in the IM bias (Section 3.2)] and there is contribution from dv / dr as well (Kaiser 1987). It is thus clear that the redshifts must be corrected to distances and that any uncertainty in v(x) at large x or at x = 0 would confuse the derived g(0). The latter is the Kaiser ``rocket effect'': if v(0) originates from a finite volume r < r₀ and the density outside r₀ is uniform with v = 0, then the measurements in z-space introduce a fake g(0) in the direction of v(0) due to the matter outside r₀, and this g(0) is logarithmically diverging with r. v(0) is uncertain because it is derived like the rest of v(x) from the density distribution - not from the CMB dipole. These difficulties in identifying convergence limit the effectiveness of this method in determining the PS on large scales and . The hopes for improvement by increasing the depth are not high because the signal according to conventional PS models drops with distance faster than the shot-noise.

Attempting to measure _I from the IRAS data, Strauss et al. (1992b) computed the probability distribution of g(0) under several models for the statistics of fluctuations, via a self-consistent solution for the velocities and an ad hoc fix to the rocket effect, which enabled partial corrections for shot-noise, finite volume, and small-scale non-linear effects. They confirmed that the direction of g(0) converges to a direction only ~ 20° away from the CMB dipole, but were unable to determine unambiguously whether |g(0)| converges even within 100 h^-1Mpc. A maximum likelihood fit and careful error analysis constrained _I to the range 0.4-0.85 with little sensitivity to the PS assumed. Rowan-Robinson et al. (1991, 1993) obtained from the QDOT dipole _I = 0.8^+0.2_-0.15. Hudson's (1993b) best estimate from the optical dipole is _opt = 0.72^+0.37_-0.18.

The volume-limited Abell/ACO catalog of clusters with redshifts within 300 h^-1Mpc was used to compute g(0) in a similar way under the assumption that clusters trace mass linearly (Scaramella et al. 1991). An apparent convergence was found by ~ 180 h^-1Mpc to the value g(0) 4860_c km s^-1. A comparison with the LG-CMB motion of 600 km s^-1 yields _c 0.123, which corresponds to _opt 0.44 and _I 0.56 if the ratios of biasing factors are 4.5:1.3:1 (Section 7.1). A similar analysis by Plionis & Valdarnini (1991) yielded convergence by ~ 150 h^-1Mpc and values larger by ~ 30-80%.

8.2 from Galaxy Density versus Velocities

The linear correlation found between mass density and galaxy density (Section 6.2) can be used to estimate the ratio . The density _v determined by POTENT from velocities assuming = 1 relates in linear theory to the true by _v f(), while linear biasing assumes = b^-1 _g, so _v = _g. Dekel et al. (1993) carried out a careful likelihood analysis using the POTENT mass density from the Mark II velocity data and the density of IRAS 1.9 Jy galaxies, and found _I = 1.3_-0.6^+0.75 at 95% confidence. A similar analysis based on the Mark III and IRAS 1.2 Jy is in progress. The degeneracy of and b is broken in the quasi-linear regime, where (v) is no longer f^-1. The compatible quasi-linear corrections in POTENT and in the IRAS analysis allow a preliminary attempt to separate these parameters, which yields for Mark II data > 0.46 (95% level) if b_I > 0.5. A correction for IM bias could reduce the 95% confidence limit to > 0.3 at most. These results are valid for linear biasing; possible non-linear biasing may complicate the analysis because it is hard to distinguish from non-linear gravitational effects.

The advantage of comparing densities is that they are local, independent of reference frame, and can be reasonably corrected for non-linear effects. The comparison can alternatively be done between the observed velocities and those predicted from a redshift survey, subject to limited knowledge of the quadrupole and higher moments of the mass distribution outside the surveyed volume and other biases. Kaiser et al. (1991) obtained from Mark II velocities versus QDOT predictions _I = 0.9^+0.20_-0.15. An analysis by Roth (1994) using IRAS 1.9 Jy galaxies yielded _I = 0.6 ± 0.3 (2). Nusser & Davis (1994) implemented a novel method based on the Zel'dovich approximation in spherical harmonics to predict the velocity dipole of distant shells from the IRAS 1.2 Jy redshift survey and found in comparison to the dipoles derived from observed velocities = 0.6 ± 0.2.

Similar comparisons with the optical galaxy fields indicate a similar correlation between light and mass. A comparison at the velocity level gives (Hudson 1994) _opt = 0.5 ± 0.1, and a preliminary comparison at the density level with 12 h^-1Mpc smoothing indicates (Hudson et al. 1994) _opt 0.75 ± 0.2, in general agreement with the ratio of b_opt / b_I 1.3-1.4 obtained by direct comparison. Shaya et al. (1994) applied the least-action reconstruction method (Section 7.2) to a redshift survey of several hundred spirals within our local 30 h^-1Mpc neighborhood and crudely obtained by comparison to TF distances _opt ~ 0.4.

8.3 from Distortions in Redshift Space

Redshift samples, which contain hidden information about velocities, can be used on their own to measure . The clustering, assumed isotropic in real space, x, is anisotropic in z-space, z, where z = r + xhat · v displaces galaxies along the preferred direction xhat. While virial velocities on small scales stretch clusters into ``fingers of god'' along the line of sight, systematic infall motions enhance large-scale structures by artificially squashing them along the line of sight. The linear approximation - · v = _g indicates that the effect is -dependent because - · v is related to the anisotropy in z-space while _g is isotropic, so the statistical deviations from isotropy can tell (e.g. Sargent & Turner 1977).

Kaiser (1987) showed in linear theory that the anisotropic Fourier PS in z-space is related to the real-space PS of mass density, P (k), via

P^z (k, µ)= P (k) (1 + µ²)², (25)

where µ khat · xhat. This relation is valid only for a fixed µ, i.e., in a distant volume of small solid angle (Zaroubi & Hoffman 1994), but there are ways to apply it more generally. The redshift PS can be decomposed into Legendre polynomials, P_l (µ), with even multipole moments P_l^z (k),

P ^z (k, µ) = _l=0 P_l^z (k) P_l (µ),

P_l^z (k) = (2l + 1) / 2 _-1⁺¹ dµ P^z (k, µ) P_l (µ). (26)

Based on Equation (25) the first two non-vanishing moments are

P₀^z (k) = (1 + (2 / 3) + (1 / 5) ²) P (k),

P₂^z (k) = ((4 / 3) + (4 / 7) ²) P (k), (27)

so the observable ratio of quadrupole to monopole is a function of independent of P (k). A preliminary application to the 1.2 Jy IRAS survey yields _I ~ 0.3-0.4 at wavelength 30-40 h^-1Mpc, suspected of being an underestimate because of non-linear effects out to ~ 50 h^-1Mpc (Cole et al. 1993). Peacock & Dodds (1994) developed a method for reconstructing the linear PS and they obtain _I = 1.0 ± 0.2.

The distortions should be apparent in the z-space two-point correlation function, _z (r_p, ), which is the excess of pairs with separation along the line of sight and r_p transversely (Davis & Peebles 1983). The contours of equal , assumed round in r-space, appear in z-space elongated along the line of sight at small separations and squashed on large scales depending on . Hamilton (1992; 1993) used the multiple moments of _z, in analogy to Equations (26-27), and his various estimates from the 1.9 Jy IRAS survey span the range _I = 0.25-1. Fisher et al. (1994a) computed ^z(r_p, ) from the 1.2 Jy IRAS survey, and derived the first two pair-velocity moments. Their attempt to use the velocity dispersion via the Cosmic Virial Theorem led to the conclusion that this is a bad method for estimating , but the mean, < v₁₂ > = 109⁺⁶⁴_-47 at 10 h^-1Mpc, yielded _I = 0.45^+0.27_-0.18. The drawbacks of using versus PS are that (a) the uncertainty in the mean density affects all scales in whereas it is limited to the k = 0 mode of the PS, (b) the errors on different scales in are correlated whereas they are independent in a linear PS for a Gaussian field, and (c) mixes different physical scales, complicating the transition between the linear and non-linear regimes. Non-linear effects tend to make all the above results underestimates.

A promising method that is tailored to deal with a realistic redshift survey of a selection function (r) and does not rely on the subtleties of Equation (25) is based on a weighted spherical harmonic decomposition of _z(z) (Fisher et al. 1994b),

a _lm^z = d ³ z (r) f (z) [1 + _z(z)] Y_lm(zhat),

< |a _lm^z| ² > = (2/) ₀ dk k² P (k) | _l^r (k) + _l^c (k) | ². (28)

The arbitrary weighting function f (z) is vanishing at infinity to eliminate surface terms. The mean-square of the harmonics is derived in linear theory assuming that the survey is a ``fair'' sample, and ^r and ^c are explicit integrals over r of certain expressions involving (r), f (r), Bessel functions and their derivatives. The first term represents real structure and the second is the correction embodying the z-space distortions. The harmonic PS in z-space, averaged over m, is thus determined by P (k) and , where the z-space distortions appear as a -dependent excess at small l. The harmonic PS derived from the 1.2 Jy IRAS survey yields _I = 1.0 ± 0.3 for an assumed ₈ = 0.7 (motivated by the IRAS , Fisher et al. 1994a), with an additional systematic uncertainty of ± 0.2 arising from the unknown shape of the PS.

The methods for measuring from redshift distortions are promising because they are relatively free of systematic errors and because very large redshift surveys are achievable in the near future. With a sufficiently large redshift survey, one can even hope to be able to use the non-linear effects to determine and b separately.

8.4 from PDFs using velocities

Assuming that the initial fluctuations are a random Gaussian field, the one-point PDF of smoothed density develops a characteristic skewness due to non-linear effects early in the quasi-linear regime (Section 7.2). The skewness of is given in second-order perturbation theory by < ³ > / < ² >² (34/7 - 3 - n), where n is the effective power index near the smoothing scale (Bouchet et al. 1992). Since this ratio for is practically independent of , and since · v ~ -f, the corresponding ratio for · v strongly depends on , and in second-order (Bernardeau et al. 1994).

T₃ < ( · v)³ > / < ( · v)² >² -f()^-1 (26 / 7 - 3 - n). (29)

Using N-body simulations and 12 h^-1Mpc smoothing one indeed finds T₃ = -1.8 ± 0.7 for = 1 and T₃ = -4.1 ± 1.3 for = 0.3, where the quoted error is the cosmic scatter for a sphere of radius 40 h^-1Mpc in a CDM universe (H₀ = 75, b = 1). A preliminary estimate of T₃ in the current POTENT velocity field within 40 h^-1Mpc is -1.1 ± 0.8, the error representing distance errors. With the two errors added in quadrature, = 0.3 is rejected at the ~ 2 level (somewhat sensitive to the assumed PS).

Since the PDF contains only part of the information stored in the data and is in some cases not that sensitive to the IPDF (Section 7.2), a more powerful bound can be obtained by using the detailed v(x) to recover the IPDF, and use the latter to constrain . This is done by comparing the -dependent IPDF recovered from observed velocities to an assumed IPDF (Nusser & Dekel 1993), most naturally a Gaussian as recovered from IRAS density (Section 7.2). The velocity out of POTENT Mark II within a conservatively selected volume was fed into the IPDF recovery procedure with either 1 or 0.3, and the errors due to distance errors and cosmic scatter were estimated. The IPDF recovered with = 1 is found marginally consistent with Gaussian while the one recovered with = 0.3 shows significant deviations. The largest deviation bin by bin in the IPDF is ~ 2 for = 1 and > 4 for = 0.3, and a similar rejection is obtained with a ²-type statistic. The skewness and kurtosis are poorly determined because of noisy tails but the replacements < x|x| > and < |x| > allow a rejection of = 0.3 at the (5-6) levels.

8.5 from Velocities in Voids

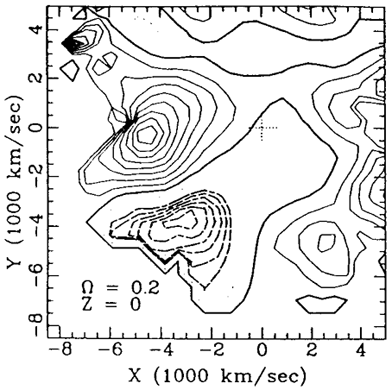
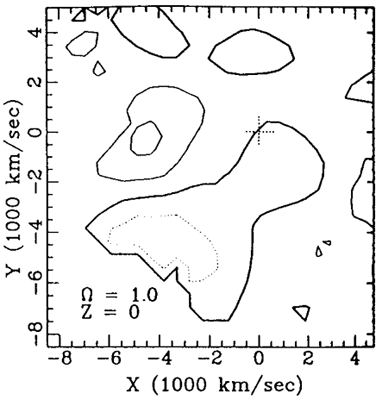
Figure 8. Maps of c inferred from the observed velocities near the Sculptor void in the Supergalactic plane, for two values of . The LG is marked by '+' and the void is confined by the Pavo part of the GA (left) and the Aquarius extension of PP (right). Contour spacing is 0.5, with c = 0 heavy, c > 0 solid, and c < 0 dotted. The heavy-dashed contours mark the illegitimate downward deviation of c below -1 in units of , starting from zero (i.e., c = -1), and decreasing with spacing -0.5. The value = 0.2 is ruled out at the 2.9 level (Dekel & Rees 1994).

A diverging flow in an extended low-density region can provide a robust dynamical lower bound on , based on the fact that large outflows are not expected in a low- universe (Dekel & Rees 1994). The velocities are assumed to be induced by GI, but no assumptions need to be made regarding galaxy biasing or the exact statistical nature of the fluctuations. The derivatives of a diverging velocity field infer a non-linear approximation to the mass density, _c(, ðv / ðx) (Equation 6), which is an overestimate, _c > , when the true value of is assumed. Analogously to ₀ = -f()^-1 · v, the _c inferred from a given diverging velocity field becomes more negative when a smaller is assumed, and it may become smaller than -1. The value of is bounded from below because mass is never negative, -1.

The inferred _c(x) smoothed at 12 h^-1Mpc and the associated error field are derived by POTENT from the observed radial velocities and, focusing on the deepest density wells, the assumed is lowered until _c becomes significantly smaller than -1. The most promising ``test case'' provided by the Mark III data seems to be a broad diverging region centered near the supergalactic plane at the vicinity of (X, Y) = (-25, -40) in h<sup>-1</sup>Mpc - the ``Sculptor void'' of galaxies (Kauffman et al. 1991) next to the ``Southern Wall'' (Figure 8). Values of 1 are perfectly consistent with the data, but _c becomes smaller than -1 already for = 0.6. The values = 0.3 and 0.2 are ruled out at the 2.4-, and 2.9 levels in terms of the random error . This is just a preliminary result. The systematic errors have been partially corrected for in POTENT, but a more specific investigation of the SG biases affecting the smoothed velocity field in density wells is required. For the method to be effective one needs to find a void that is (a) bigger than the correlation length for its vicinity to represent the universal , (b) deep enough for the lower bound to be tight, (c) nearby enough for the distance errors to be small, and (d) properly sampled to trace the velocity field in its vicinity.

The estimates of and are summarized in Table 1.

Table 1. and b¹

CMB dipole	vs galaxies angular	Yahil et al.86	I = 0.9 ± 0.22
	vs galaxies redshift	Strauss et al. 92b	I = 0.4 - 0.85
		Rowan-Rob. et al. 91	I = 0.8+0.2-0.15
	vs galaxies angular	Lynden-Bell et al. 89	opt = 0.1 - 0.5
	vs galaxies redshift	Hudson 93b	opt = 0.7+0.4-0.2
	clusters	Scaramella et al. 91	c ~ 0.13
		Plionis et al. 91	c ~ 0.17-0.22
v vs g	Potent-IRAS1.9 density	Dekel et al.93	I = 1.3+0.75-0.6 (95%)
	Potent-IRAS1.2 v-dipole	Nusser & Davis 94	I = 0.6 ± 0.2
	TF-QDOT	Kaiser et al. 91	I = 0.9+0.2-0.15
	TF-QDOT clusters	Frenk et al. 94	I = 1.0 ± 0.3
	TF inverse - IRAS1.9	Roth 94	I = 0.6 ± 0.35 (2)
	Potent-Optical density	Hudson et al. 94	opt = 0.75 ± 0.2
	TF-Optical	Hudson 94	opt = 0.5 ± 0.1
	TF-Optical local	Shaya et al. 94	opt ~ 0.4
z-distortions	Pk IRAS1.2	Cole et al. 93	I 0.3-0.4
	Pk IRAS1.2	Peacock & Dodds 94	I = 1.0 ± 0.2
	IRAS1.9	Hamilton 93	I ~ 0.25 - 1
	IRAS1.2	Fisher et al. 94a	I = 0.45+0.3-0.2
	Ylm IRAS1.2	Fisher et al. 94b	I = 1.0 ± 0.3
Velocities	Gaussian IPDF Potent	Nusser & Dekel 93	> 0.3 (4 - 6)
	Skew ( · v) Potent	Bernardeau et al. 94	> 0.3 (2)
	Voids Potent	Dekel & Rees 94	> 0.3 (2.4)