Copyright © 1994 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1994. 32:
371-418 Copyright © 1994 by Annual Reviews. All rights reserved |
Having assumed GI, the LSS can be traced backward in time to recover the
initial fluctuations and constrain statistics which characterize them as
a random field, e.g. the power spectrum (PS), and the probability
distribution functions (PDFs). ``Initial'' here may refer either
to the linear regime at z ~ 103 after the onset of the
self-gravitating matter
era, or to the origin of fluctuations in the early universe before
being filtered on sub-horizon scales during the plasma-radiation era.
The PS is filtered on scales  100 h-1Mpc by DM-dominated
processes, but its shape on scales
100 h-1Mpc by DM-dominated
processes, but its shape on scales  10 h-1Mpc is not
affected much by recent non-linear effects (because the rapid density
evolution in superclusters roughly balances the slow evolution in voids
at the same wavelength). The shape of the one-point PDF, on the other
hand, is expected to survive
the plasma era unchanged but it develops strong skewness even in the
mildly-non-linear regime. Thus, the present day PS can be used as is to
constrain the origin of fluctuations (large scale) and the nature of the
DM (small scale), while the PDF needs to be traced back to the linear
regime first. (Review: Efstathiou 1990.)
10 h-1Mpc is not
affected much by recent non-linear effects (because the rapid density
evolution in superclusters roughly balances the slow evolution in voids
at the same wavelength). The shape of the one-point PDF, on the other
hand, is expected to survive
the plasma era unchanged but it develops strong skewness even in the
mildly-non-linear regime. Thus, the present day PS can be used as is to
constrain the origin of fluctuations (large scale) and the nature of the
DM (small scale), while the PDF needs to be traced back to the linear
regime first. (Review: Efstathiou 1990.)
The competing LSS formation scenarios are reviewed in
Peebles (1993, Section
25). If the DM is all baryonic, then by nucleosynthesis constraints
(see Kolb & Turner 1990,
Section 4) the universe must be of low density,
 < 0.2, and a viable
model for LSS is the Primordial
Isocurvature Baryonic model (PIB) with several free parameters,
typically of large relative power on large scales. With
< 0.2, and a viable
model for LSS is the Primordial
Isocurvature Baryonic model (PIB) with several free parameters,
typically of large relative power on large scales. With
 ~ 1 the non-baryonic DM
constituents are either ``hot'' or
``cold'', and the main competing models are CDM, HDM, and MDM - a 7:3
mixture of the two (e.g.
Blumenthal et al. 1988;
Davis et al. 1992;
Klypin et al. 1993). The
main difference in the DM effect on the PS arises
from free-streaming damping of the ``hot'' component of fluctuations on
galactic scales.
~ 1 the non-baryonic DM
constituents are either ``hot'' or
``cold'', and the main competing models are CDM, HDM, and MDM - a 7:3
mixture of the two (e.g.
Blumenthal et al. 1988;
Davis et al. 1992;
Klypin et al. 1993). The
main difference in the DM effect on the PS arises
from free-streaming damping of the ``hot'' component of fluctuations on
galactic scales.
BULK VELOCITY. A simple and robust statistic related to the PS is the amplitude V of the vector average of the smoothed velocity field, v, over a volume defined by a normalized window function WR(r) of a characteristic scale R (e.g. top-hat),
< V2 > is predicted for a linear model with a density
spectrum P (k), where tilde
WR2(k), the Fourier transform of
WR (r),
emphasizes waves
MACH NUMBER. The bulk velocity is robust but it relates to
the normalization of the PS, not predicted from first
principles by any of the competing theories but rather normalized
by some other uncertain observation, e.g. the CMB fluctuations or
the galaxy distribution with an unknown biasing factor. A
statistic which measures the shape of the PS
free of its normalization is the
cosmic Mach number
(Ostriker & Suto 1990), defined
as M
M(R, Rs) measures the
ratio of power on large
scales
POWER SPECTRUM. The velocity field by POTENT enables a
preliminary determination of the mass PS itself in the range
10-100 h-1Mpc
(Kolatt & Dekel 1994b). It is
best determined by
the potential field, which is smoother and less sensitive to non-linear
effects than its derivatives v and
A DISCREPANCY ON A VERY LARGE SCALE? The galaxy velocity field in
the local ~ 60 h-1Mpc which has been studied quite accurately
seems to be in general agreement with other observations and with the
predictions of the common GI scenarios, but there is a disturbing hint
for a possible discrepancy with our basic hypotheses on larger scales.
Lauer and Postman (1993, LP) measured the bulk flow of the volume-limited
system of 119 Abell/ACO clusters within z < 150 h-1Mpc,
estimating distances from luminosity versus slope of the
surface-brightness profile in brightest cluster galaxies (BCG) with
claimed 16% error. The LG motion with respect to this system is found
to be 561 ± 284 km s-1 towards (l, b) =
(220°,-28°), roughly 80° off the direction of the LG-CMB
velocity (276°,+30°). The inferred bulk velocity of the cluster
system (of effective radius ~ 80-110 h-1Mpc)
relative to the CMB is V = 689 ± 178 km s-1
towards (343°,+52°)
(± 23°), in the general direction of the LG motion,
the galaxy bulk flow, the GA and the
background Shapley concentration. Taken at face value this is a
high velocity over a large scale; the rms bulk velocity within
R = 100 h-1Mpc as predicted by the common theories
normalized to COBE is below 200 km s-1. However, the
errors are large too.
The data have been subjected by LP to careful statistical tests. With a
few tens of points contributing to the velocity in each direction, the
shot-noise can clearly contribute a false signal of several
hundred km s-1. For assessing the theoretical implications,
the actual observing scheme of LP was applied to N-body
simulations of several competing scenarios
(Strauss et al. 1994).
Clusters were placed at the 119 highest density peaks of appropriate mass, and
Galactic extinction and observational errors were modeled. As noted by
LP, the fact that the measured velocity vector lies away from the ZOA
increases the statistical significance of this measurement. Taking the
error ellipsoid into account, the probability by means of
A true ~ 700 km s-1 velocity at R ~ 100
h-1Mpc would be in serious conflict with GI. First, if this
velocity is typical then it predicts larger CMB fluctuations than
observed on ~ 2°. Second, the gravitational acceleration on the LP
sphere as estimated from
the spatial distribution of clusters on even larger scales
(Section 8.1,
Scaramella et al. 1991)
predicts a flow of only ~ 200 km
s-1. The way to interpret the LP result in the context
of the conventional theories is either as a
~ 2-2.5
The forward integration of the GI equations by analytic approximations or
by N-body simulations
cannot be simply reversed despite the time reversiblity of gravity. It
is especially hopeless in collapsed systems where memory has been erased,
but the case is problematic even for linear systems. When attempting
backwards integration, the decaying modes (e.g.
Peebles 1993,
Section 5), having left no detectable
trace at present, t0,
would amplify noise into dominant spurious fluctuations at early
times. This procedure has a negligible probability of recovering the
very special initial state of almost uniform density and tiny velocities
which we assume for the real universe at ti.
This is a problem of mixed boundary conditions: some of the six
phase-space variables per particle
are given at ti and some at t0. This
problem can be solved either by eliminating the decaying modes
or by applying the principle of least action.
ZEL'DOVICH TIME MACHINES. If the velocity field is irrotational,
the Euler equation (2) can be replaced by the Bernoulli equation for the
potentials,
dot
RECOVERING THE IPDF. An important issue is whether or not the initial
fluctuations were Gaussian. A Gaussian field is characterized by
the joint PDFs of all order being generalized Gaussians (cf.,
Bardeen et al. 1986), and
in particular the one-point probability of
The observed PDFs today
agree with N-body simulations of Gaussian initial
conditions
(Bouchet et al. 1993),
but they have only limited
discriminatory power against initial non-Gaussianities; the development of
a density PDF with a general log-normal shape may occur even in certain
cases of non-Gaussian initial fluctuations (e.g.
Weinberg & Cole 1992), and the
velocity PDF becomes
Gaussian under general conditions due to the central limit theorem
whenever the velocity is generated by several independent
density structures. A more effective strategy seems to be to take
advantage of the full dynamical fields at t0, trace
them back in time, and use the linear fields to discriminate between
theories. The Eulerian Zel'dovich
approximation can be used to directly recover the initial PDF
(IPDF) as follows
(Nusser & Dekel 1993). The
tensor ð vi / ð xj derived
from v(x) is
transformed to Lagrangian variables q(x). The corresponding
eigenvalues µi
A key feature of the recovered IPDF is that it is sensitive to the
assumed value of
GAUSSIANIZATION. A simple method for recovering the initial
fluctuations from the galaxy distribution under the
assumption that they were Gaussian is based on the assertion that
both gravitational evolution and biased galaxy formation tend to preserve
the rank order of density in cells. The non-Gaussian distribution of
galaxies in cells simply needs to be
``Gaussianized'' in a rank-preserving way
(Weinberg 1991). The initial
conditions
can then be evolved forward using an N-body code and compared with the
observed galaxy distribution in z-space until convergence. A
self-consistent solution for a redshift survey in the PP region was found
if bopt ~ 2, while it was impossible
to match the structure on small and large scales simultaneously
with GI, Gaussian fluctuations and no biasing. This result derived
independently of
LEAST ACTION. The general GI problem with mixed boundary
conditions lends itself naturally to an application of Hamilton's action
principle (Peebles 1989;
1990;
1993). The comoving orbit
xi (t) of each mass point
mi is parametrized in a way that satisfies the
boundary conditions xi (t0) =
xi 0 and lim t->0
a2 dotxi = 0, and the action
is minimized to determine the free parameters. The orbits can be
xi (t) =
xi (t0) + 
 d3 x WR(x)
v(x),
d3 x WR(x)
v(x),
 2
2  0
0 dk P(k) tilde
WR2(k).
dk P(k) tilde
WR2(k).
 R.
The bulk velocity is obtained from the observed radial velocities by
minimizing Equation (11).
The report by
Dressler et al. (1987)
for the 7S Es sampled
within ~ 60 h-1Mpc was V = 599 ± 104 towards
(l, b) = (312°, +6°), which was
interpreted prematurely as
being in severe excess of the predictions of common theories.
However, this measurement cannot be directly compared to the predictions
for a top-hat sphere because the effective window is much smaller due
to the nonuniform sampling (SG) and weighting (Kaiser 1988).
The SG bias can be crudely corrected by volume weighting as in
POTENT (Section 4.2), at
the expense of large noise.
Courteau et al. (1993) find for
the tentative Mark III data: V40 = 335 ± 38
(295°, +35°) and
V60 = 360 ± 40 (279°, +11°), where
VR refers to a top-hat sphere of radius R
h-1Mpc. Alternatively, V can be computed from the
POTENT v field by simple vector averaging from the grid.
Figure 7 shows two results, one minimizing the
SG bias by Vi weighting, and the other reducing the
random errors by weighting
R.
The bulk velocity is obtained from the observed radial velocities by
minimizing Equation (11).
The report by
Dressler et al. (1987)
for the 7S Es sampled
within ~ 60 h-1Mpc was V = 599 ± 104 towards
(l, b) = (312°, +6°), which was
interpreted prematurely as
being in severe excess of the predictions of common theories.
However, this measurement cannot be directly compared to the predictions
for a top-hat sphere because the effective window is much smaller due
to the nonuniform sampling (SG) and weighting (Kaiser 1988).
The SG bias can be crudely corrected by volume weighting as in
POTENT (Section 4.2), at
the expense of large noise.
Courteau et al. (1993) find for
the tentative Mark III data: V40 = 335 ± 38
(295°, +35°) and
V60 = 360 ± 40 (279°, +11°), where
VR refers to a top-hat sphere of radius R
h-1Mpc. Alternatively, V can be computed from the
POTENT v field by simple vector averaging from the grid.
Figure 7 shows two results, one minimizing the
SG bias by Vi weighting, and the other reducing the
random errors by weighting 
 i-2
(Section 4.2).
V60 is found to be in the range 270-360 km
s-1 (296°,+11°)
- smaller than previous estimates.
The additional random error from Monte-Carlo noise simulations is typically
15%, not including cosmic scatter due to the fact that only one sphere
has been sampled.
i-2
(Section 4.2).
V60 is found to be in the range 270-360 km
s-1 (296°,+11°)
- smaller than previous estimates.
The additional random error from Monte-Carlo noise simulations is typically
15%, not including cosmic scatter due to the fact that only one sphere
has been sampled.
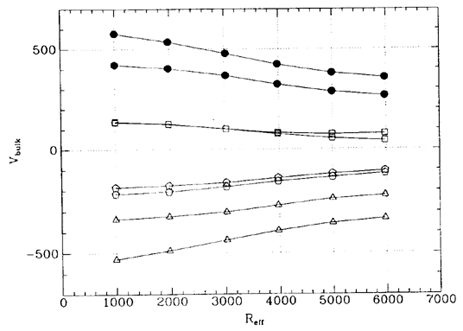
Figure 7. The bulk velocity in a top-hat sphere of radius
Reff about the LG
as recovered by POTENT from the Mark III data. Shown are |V|
(filled dots), Vx (triangles), Vy
(squares), and Vz
(hexagons). Distances and velocities are in km s-1. The two
results shown reflect the systematic uncertainty. The 1  uncertainty due to random distance
errors is
uncertainty due to random distance
errors is  15%
(Dekel et al. 1994).
15%
(Dekel et al. 1994).
 V / S, where
S is the rms deviation of the local velocity from
the bulk velocity,
V / S, where
S is the rms deviation of the local velocity from
the bulk velocity,

 d3 x
WR(x)
[v(x)-v]2,
d3 x
WR(x)
[v(x)-v]2,
 2
2  0
0 dk P (k) [1 -
tildeWR2(k)].
dk P (k) [1 -
tildeWR2(k)].
 R
to power on small scales
R
to power on small scales  Rs.
Strauss et al. (1993)
derived M =
1.0 for the local Ss
(Aaronson et al. 1982a)
with R ~ 20
h-1Mpc and Rs -> 0, and found ~ 5% of their
CDM simulations
to have M as large - a marginal
rejection or consistency depending on taste. On larger scales, using
POTENT with R = 60 h-1Mpc (top-hat) and
Rs = 12 h-1Mpc (Gaussian), the tentative Mark III
data yield M ~ 1, which roughly
coincides with the rms expected from CDM but has only ~ 5% probability to be
that low for a PIB spectrum
(
Rs.
Strauss et al. (1993)
derived M =
1.0 for the local Ss
(Aaronson et al. 1982a)
with R ~ 20
h-1Mpc and Rs -> 0, and found ~ 5% of their
CDM simulations
to have M as large - a marginal
rejection or consistency depending on taste. On larger scales, using
POTENT with R = 60 h-1Mpc (top-hat) and
Rs = 12 h-1Mpc (Gaussian), the tentative Mark III
data yield M ~ 1, which roughly
coincides with the rms expected from CDM but has only ~ 5% probability to be
that low for a PIB spectrum
( = 0.1, h = 1,
fully ionized, normalized to
= 0.1, h = 1,
fully ionized, normalized to  8 = 1)
(Kolatt et al., in preparation).
8 = 1)
(Kolatt et al., in preparation).
 . The PS
was compared with the predictions of theoretical models which were
N-body simulated, ``observed'', and fed into POTENT before the
PS was computed using the same procedure applied to the observed
data, thus eliminating the effect of systematic errors and estimating
the random errors. The preliminary results indicate that
the shape of the PS in the limited range sampled resembles a
CDM-like PS with a shape parameter
. The PS
was compared with the predictions of theoretical models which were
N-body simulated, ``observed'', and fed into POTENT before the
PS was computed using the same procedure applied to the observed
data, thus eliminating the effect of systematic errors and estimating
the random errors. The preliminary results indicate that
the shape of the PS in the limited range sampled resembles a
CDM-like PS with a shape parameter
 ~ 0.5 (referring in CDM
to
~ 0.5 (referring in CDM
to  h),
with the power index bending toward n
h),
with the power index bending toward n  0 by 100 h-1Mpc.
The normalization for the mass PS,
also obtained by
Seljak & Bertschinger (1994),
is f
0 by 100 h-1Mpc.
The normalization for the mass PS,
also obtained by
Seljak & Bertschinger (1994),
is f  8
= 1.3 ± 0.3. This is not too sensitive to the PS shape,
but still note that it mostly determined by data at ~ 30 h-1Mpc.
With
8
= 1.3 ± 0.3. This is not too sensitive to the PS shape,
but still note that it mostly determined by data at ~ 30 h-1Mpc.
With  8opt
8opt  1 for optical
galaxies, this implies
1 for optical
galaxies, this implies  opt
opt  1.3 ± 0.3 (compare Section 8).
If
1.3 ± 0.3 (compare Section 8).
If  = 1, the quadrupole
in
= 1, the quadrupole
in  T / T by COBE
corresponds to
T / T by COBE
corresponds to
 8 = 1.0, 0.6,
0.5 with ~ 45% error (including cosmic scatter)
for CDM, MDM and HDM
spectra (yet to be calculated for an open universe), i.e., CDM is fine
while HDM and MDM are ~ 2
8 = 1.0, 0.6,
0.5 with ~ 45% error (including cosmic scatter)
for CDM, MDM and HDM
spectra (yet to be calculated for an open universe), i.e., CDM is fine
while HDM and MDM are ~ 2 low.
In comparison, the PS of the different luminous objects are all well described
by a CDM-like PS with
low.
In comparison, the PS of the different luminous objects are all well described
by a CDM-like PS with 
 0.25,
with the relative bias factors for Abell clusters, optical galaxies and
IRAS
galaxies in the ratios 4.5:1.3:1 (± 6% rms, e.g.
Peacock & Dodds 1994). If indeed
0.25,
with the relative bias factors for Abell clusters, optical galaxies and
IRAS
galaxies in the ratios 4.5:1.3:1 (± 6% rms, e.g.
Peacock & Dodds 1994). If indeed
 8opt ~ 1 for
optical galaxies, then
IRAS galaxies are slightly anti-biased and
8opt ~ 1 for
optical galaxies, then
IRAS galaxies are slightly anti-biased and
 I
I
 1.3.
1.3. opt.
opt.
 2 of the LP result in
the model universes simulated is 2.6-5.8%.
Feldman & Watkins (1994), using
a different technique, find the
probabilities to be 6-10%. The LP bulk velocity is thus a
~ 2
2 of the LP result in
the model universes simulated is 2.6-5.8%.
Feldman & Watkins (1994), using
a different technique, find the
probabilities to be 6-10%. The LP bulk velocity is thus a
~ 2 deviation from
several common theories. This is probably not enough for a serious
falsification of these models,
but it is certainly an intriguing result which motivates more accurate
investigations. The BCG method is limited to one measurement per
cluster, so an obvious strategy to reduce the errors would be to collect
many TF and Dn
-
deviation from
several common theories. This is probably not enough for a serious
falsification of these models,
but it is certainly an intriguing result which motivates more accurate
investigations. The BCG method is limited to one measurement per
cluster, so an obvious strategy to reduce the errors would be to collect
many TF and Dn
-  distances per cluster.
distances per cluster.
 statistical
fluke, or as a biased result due to a yet-unresolved systematic error in
the BCG method or in the sample, e.g. a
significant velocity biasing of the clusters (which is contrary to the
naive expectations from GI, however).
statistical
fluke, or as a biased result due to a yet-unresolved systematic error in
the BCG method or in the sample, e.g. a
significant velocity biasing of the clusters (which is contrary to the
naive expectations from GI, however).
7.2 Back in Time
 v -
(
v -
(
 v)2/2
= -2H
v)2/2
= -2H  v +
v +  g. The Zel'dovich approximation, restricted
to the growing mode, requires that each side vanish: one side
relates
g. The Zel'dovich approximation, restricted
to the growing mode, requires that each side vanish: one side
relates  v and
v and
 g linearly
and the other is the ``Zel'dovich-Bernoulli'' (ZB)
equation (Nusser & Dekel 1992),
dot
g linearly
and the other is the ``Zel'dovich-Bernoulli'' (ZB)
equation (Nusser & Dekel 1992),
dot v - (Ddot / 2) (
v - (Ddot / 2) (
 v)2 = 0,
with the potentials in units of a2Ddot. The ZB
equation can be easily integrated
backwards with a guaranteed uniform solution at ti.
v)2 = 0,
with the potentials in units of a2Ddot. The ZB
equation can be easily integrated
backwards with a guaranteed uniform solution at ti.
 v at
t0 is extractable from observations of velocities
(Section 4) or galaxy density
(Section 5), and the initial v and
v at
t0 is extractable from observations of velocities
(Section 4) or galaxy density
(Section 5), and the initial v and
 can be derived from
the initial
can be derived from
the initial  v using linear theory. While the ZB
approximation conserves
momentum (like
v using linear theory. While the ZB
approximation conserves
momentum (like  0) one can alternatively satisfy continuity
under the Zel'dovich approximation (like
0) one can alternatively satisfy continuity
under the Zel'dovich approximation (like  c), and obtain a
second-order equation for
c), and obtain a
second-order equation for  g which is somewhat more accurate
(Gramman 1993b,
Equation 2.24, 2.25). The recovered initial
g which is somewhat more accurate
(Gramman 1993b,
Equation 2.24, 2.25). The recovered initial  i has
deeper valleys and shallower hills compared to naive recovery using
linear theory, e.g. the GA is less eccentric
than assumed by
Bertschinger & Juszkiewicz (1988).
i has
deeper valleys and shallower hills compared to naive recovery using
linear theory, e.g. the GA is less eccentric
than assumed by
Bertschinger & Juszkiewicz (1988).
 is
P(
is
P( )
) exp[-
exp[- 2 / (2
2 / (2 2)]. Common
Inflation predicts Gaussian fluctuations but non-Gaussian fluctuations
are allowed by certain versions of Inflation (cf.,
Kofman et al. 1990) and
by models where the perturbations are seeded by cosmic strings,
textures, or explosions (see
Peebles 1993, Section 16). The
present density PDF develops a log-normal shape
due to non-linear effects
(Coles & Jones 1991;
Kofman et al. 1994): the
tails become positively skewed because peaks collapse to large densities
while the density in voids cannot become negative, and the middle
develops negative skewness as density hills contract and valleys expand.
On the other hand, the PDF of present-day velocity components is insensitive
to quasi-linear effects
(Kofman et al. 1994).
2)]. Common
Inflation predicts Gaussian fluctuations but non-Gaussian fluctuations
are allowed by certain versions of Inflation (cf.,
Kofman et al. 1990) and
by models where the perturbations are seeded by cosmic strings,
textures, or explosions (see
Peebles 1993, Section 16). The
present density PDF develops a log-normal shape
due to non-linear effects
(Coles & Jones 1991;
Kofman et al. 1994): the
tails become positively skewed because peaks collapse to large densities
while the density in voids cannot become negative, and the middle
develops negative skewness as density hills contract and valleys expand.
On the other hand, the PDF of present-day velocity components is insensitive
to quasi-linear effects
(Kofman et al. 1994).
 ð vi
/ ð xi and
ð vi
/ ð xi and  i
i  ð vi / ð qi are
related via the key relation
ð vi / ð qi are
related via the key relation  i = µi / (1 -
f-1µi).
In the Zel'dovich approximation v
i = µi / (1 -
f-1µi).
In the Zel'dovich approximation v  Ddot so the Lagrangian
derivatives
Ddot so the Lagrangian
derivatives  i are traced back in time by simple scaling
i are traced back in time by simple scaling
 Ddot-1. The initial densities at q(x)
can then be computed using linear theory,
Ddot-1. The initial densities at q(x)
can then be computed using linear theory,
 in
in  - (
- ( 1 +
1 +  2 +
2 +  3), and
the IPDF is computed by bin counting of
3), and
the IPDF is computed by bin counting of  in values across the
Eulerian grid, weighted by the present densities at the grid points.
in values across the
Eulerian grid, weighted by the present densities at the grid points.
 when
the input data is velocities (Section 8.4), and
is
when
the input data is velocities (Section 8.4), and
is  -independent if the
input is density. Thus it can be used to robustly
recover the IPDF from the density field of the 1.2 Jy IRAS survey
(Nusser et al. 1994).
The IPDF so determined is
insensitive to galaxy biasing in the range 0.5
-independent if the
input is density. Thus it can be used to robustly
recover the IPDF from the density field of the 1.2 Jy IRAS survey
(Nusser et al. 1994).
The IPDF so determined is
insensitive to galaxy biasing in the range 0.5  b
b  2, at least for the power-law
biasing relation assumed. Errors were evaluated using mock IRAS-like
catalogs, and the IPDF was found to be consistent with Gaussian,
e.g. the initial skewness S
and kurtosis K are limited at the 3
2, at least for the power-law
biasing relation assumed. Errors were evaluated using mock IRAS-like
catalogs, and the IPDF was found to be consistent with Gaussian,
e.g. the initial skewness S
and kurtosis K are limited at the 3 level to -0.65 < S < 0.36 and
-0.82 < K < 0.62 - useful for evaluating specific non-Gaussian models.
The first-year COBE measurements are consistent with Gaussian but the
noise limits their discriminatory power to strongly
non-Gaussian models
(Smoot et al. 1994).
level to -0.65 < S < 0.36 and
-0.82 < K < 0.62 - useful for evaluating specific non-Gaussian models.
The first-year COBE measurements are consistent with Gaussian but the
noise limits their discriminatory power to strongly
non-Gaussian models
(Smoot et al. 1994).
 implies
a high
implies
a high  once
once  opt is
determined by another method (Section 8), but
note that the limited surveyed region may be an ``unfair'' sample.
opt is
determined by another method (Section 8), but
note that the limited surveyed region may be an ``unfair'' sample.
 0t0 L dt =
0t0 L dt =
 0t0 dt
0t0 dt  i
[(1/2)mi a2
dotxi2 - mi
i
[(1/2)mi a2
dotxi2 - mi  g
(xi)]
g
(xi)]
 n
fn (t) Ci, n,
where fn (t) each satisfy the boundary conditions,
and Ci, n are the parameters. The
problem can be solved to any desired accuracy by increasing n, and a
proper choice of fn's helps the series to converge
rapidly to the desired solution. A generalization of the Zel'dovich
approximation of the sort fn (t) = [D (t) -
D(t0)]n
is particularly efficient
(Giavalisco et al. 1993).
In a preliminary application of this scheme to a redshift sample
(Shaya et al. 1994) the
galaxies are assumed to trace mass and be
self-gravitating. The complication caused by observing redshifts is
solved by an iterative procedure: a tentative guess is made for the
xi at t0 based on
TF
distances to a sub-sample of galaxies and a
crude flow model, and the least-action solution provides peculiar
velocities, i.e., redshifts, whose deviations from the observed redshifts
are used to correct the xi for the next
iteration, until convergence. After the original study of the history of
the Local Group
(Peebles 1989), the method was
applied to a sample based
on 500 groups within 30 h-1Mpc of the LG from the Nearby
Galaxy Catalog. The results indicate
that the unknown tidal forces from outside the sampled volume have a
significant effect on the recovered fields and should be incorporated in
future applications. The solution obtained depends on the assumed
n
fn (t) Ci, n,
where fn (t) each satisfy the boundary conditions,
and Ci, n are the parameters. The
problem can be solved to any desired accuracy by increasing n, and a
proper choice of fn's helps the series to converge
rapidly to the desired solution. A generalization of the Zel'dovich
approximation of the sort fn (t) = [D (t) -
D(t0)]n
is particularly efficient
(Giavalisco et al. 1993).
In a preliminary application of this scheme to a redshift sample
(Shaya et al. 1994) the
galaxies are assumed to trace mass and be
self-gravitating. The complication caused by observing redshifts is
solved by an iterative procedure: a tentative guess is made for the
xi at t0 based on
TF
distances to a sub-sample of galaxies and a
crude flow model, and the least-action solution provides peculiar
velocities, i.e., redshifts, whose deviations from the observed redshifts
are used to correct the xi for the next
iteration, until convergence. After the original study of the history of
the Local Group
(Peebles 1989), the method was
applied to a sample based
on 500 groups within 30 h-1Mpc of the LG from the Nearby
Galaxy Catalog. The results indicate
that the unknown tidal forces from outside the sampled volume have a
significant effect on the recovered fields and should be incorporated in
future applications. The solution obtained depends on the assumed
 , so a comparison with
independent
TF distances can in principle
constrain
, so a comparison with
independent
TF distances can in principle
constrain  (Section 8.2).
(Section 8.2).