


We adopt as our basic working hypothesis the standard cosmological model of Friedmann Robertson Walker (FRW), where we assume homogeneity and isotropy and describe gravity by general relativity. We limit the discussion to the matter-dominated era in the ``dust'' approximation.
The Friedmann equation that governs the universal expansion can be written in terms of the different contributions to the energy density (e.g., [1]):
Here, a(t) is the expansion factor of the universe,
H(t)
We denote
The FRW model also predicts a relation between the dimensionless product
H0t0 and the parameters
The global measures commonly involve combinations of the cosmological
parameters. Constraints in the
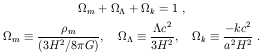

 / a is the Hubble constant,
/ a is the Hubble constant,
 m(t)
is mean the mass density,
m(t)
is mean the mass density,
 is the cosmological constant,
and k is the curvature parameter.
Hereafter, the above symbols for the cosmological parameters
refer to their values at the present time, t0.
is the cosmological constant,
and k is the curvature parameter.
Hereafter, the above symbols for the cosmological parameters
refer to their values at the present time, t0.
 tot
tot

 m +
m +

 , which by Eq. 1 equals
1 -
, which by Eq. 1 equals
1 -  k; its value
relative to unity determines whether the universe
is open (k = - 1), flat (k = 0), or closed (k = + 1).
Another quantity of interest is the deceleration parameter,
q0
k; its value
relative to unity determines whether the universe
is open (k = - 1), flat (k = 0), or closed (k = + 1).
Another quantity of interest is the deceleration parameter,
q0  -
a
-
a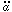 /
/
 2,
which by Eq. 1
is related to the other parameters via
q0 =
2,
which by Eq. 1
is related to the other parameters via
q0 =
 m/2 -
m/2 -

 .
.
 m and
m and

 .
For
.
For

 = 0, this product ranges
between 1 and 2/3 for
= 0, this product ranges
between 1 and 2/3 for
 m in the range 0 to
1 respectively, and it is computable for any values of
m in the range 0 to
1 respectively, and it is computable for any values of
 m and
m and

 (Section 2.5).
(Section 2.5).
 m -
m -

 plane
are displayed in Figure 1.
plane
are displayed in Figure 1.