


2.4. Microwave Background Acoustic Peaks
This is the most promising test. In less than a decade it is expected to provide the most stringent constraints on the cosmological parameters. The test uses the effect of the background cosmology on the geodesics of photons. Current ground-based and balloon-born experiments already provide preliminary constraints on the location of the first acoustic peak on sub-degree scales in the angular power spectrum of CMB temperature fluctuations, l (l + 1)Cl. The dependence of the peak location on the cosmological parameters enters via the combined effect of (a) the physical scale of the ``sound horizon'' that is proportional to the cosmological horizon at recombination, and (b) the geometry of space-time via the angular-diameter distance. In the vicinity of a flat model, the first peak is predicted at approximately the multipole (e.g., [11] [12])
New Developments:
The next generation of post-COBE CMB satellites (MAP to be launched by
NASA in 2001, and in particular COBRAS/SAMBA scheduled by ESA for 2004)
are planned to
obtain a precision at ~ 10 arc-minute resolution
that will either rule out the current framework of GI
for structure formation or
will measure the cosmological parameters to high precision.
Detailed evaluation of COBRAS/SAMBA shows that
nominal performance and expected foreground subtraction noise will
allow parameter estimation with the following accuracy:
H0 ± 1%,
Pro:
The precision hoped for is much better than attainable with any other known
method. If the observations fit the model, the precision is such that
the model will be confirmed beyond reasonable doubt.
Con:
The measurements might be messed up by unexpected foreground
contamination (e.g., by diffuse matter in galaxy groups).
Current Results:
Balloon and ground-based results have already confirmed the
existence of the first acoustic peak, and have constrained it's location
to the vicinity l ~ 200.
The results of COBE's DMR (l ~ 10) provide an upper bound of
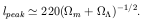
 tot ± 0.005,
tot ± 0.005,

 ± 0.02,
± 0.02,
 b ± 2%.
b ± 2%.
 The constraints on
The constraints on
 tot come mostly from
geometrical effects.
The interpretation is based on well understood physics of sound waves
in the linear regime, and on the assumption of absence of any relevant
preferred scale (in the megaparsecs to gigaparsec range)
in the physics which generated the
initial structure. The latter assumption can be checked directly by the
observations themselves.
tot come mostly from
geometrical effects.
The interpretation is based on well understood physics of sound waves
in the linear regime, and on the assumption of absence of any relevant
preferred scale (in the megaparsecs to gigaparsec range)
in the physics which generated the
initial structure. The latter assumption can be checked directly by the
observations themselves.
 The detailed measurements need to wait 5 to 10 years.
The detailed measurements need to wait 5 to 10 years.
 The assumption of no preferred scale in the initial fluctuations
may be wrong.
The assumption of no preferred scale in the initial fluctuations
may be wrong.
 If the observations do not fit the model, the whole
paradigm behind current structure formation modeling will be excluded,
and then no parameter estimates will be possible.
However, this seems unlikely given the recent measurements from the
ground and from balloons, which have already confirmed the
existence of the first acoustic peak.
If the observations do not fit the model, the whole
paradigm behind current structure formation modeling will be excluded,
and then no parameter estimates will be possible.
However, this seems unlikely given the recent measurements from the
ground and from balloons, which have already confirmed the
existence of the first acoustic peak.
 m +
m +

 < 1.5 at the 95%
confidence level
for a scale-invariant initial spectrum
(and the constraint becomes tighter for any ``redder'' spectrum,
n < 1)
[12].
Several balloon experiments (l ~ 50 - 200)
strengthen this upper bound
[13].
The CAT experiment (l ~ 350 - 700)
yields a preliminary lower bound of
< 1.5 at the 95%
confidence level
for a scale-invariant initial spectrum
(and the constraint becomes tighter for any ``redder'' spectrum,
n < 1)
[12].
Several balloon experiments (l ~ 50 - 200)
strengthen this upper bound
[13].
The CAT experiment (l ~ 350 - 700)
yields a preliminary lower bound of
 m +
m +

 > 0.3
[14]
(Fig. 1).
> 0.3
[14]
(Fig. 1).