


2.2. Classical Tests of Geometry
The parameter-dependent large-scale geometry of space-time
is reflected in the volume-redshift relation.
There are two classical versions of the tests that utilize this dependence:
magnitude versus redshift (or ``Hubble diagram'')
and number density versus redshift.
The luminosity distance to a redshift z,
which enters the Hubble diagram test,
depends on  m and
m and

 via the integral
(e.g.,
[1])
via the integral
(e.g.,
[1])
where S0(x)
New Developments:
Accumulating data of supernovae type Ia (SNIa)
out to z ~ 0.4 and beyond look promising for a
Hubble-diagram test
[3].
The preliminary success of the method may indicate that it will be able
to separate the dependences on
Pro:
The main advantage of such tests is that they are
direct measures of global geometry and thus independent
of assumptions regarding the mass type and distribution, the
statistical nature of the fluctuations, the growth by gravitational
instability (GI) and galaxy biasing.
Con:
The key question is whether SNIa are indeed a standard
candle. Some caution is in place as long as we lack
a complete theory for supernovae.
If they are exploding white dwarfs, perhaps the generic SNIa
at z ~ 1 comes from a higher mass white dwarf than one does today?
Current Results:
The first 7 supernovae analyzed by Perlmutter et al.
[3]
at z ~ 0.4 yield
-0.3 < 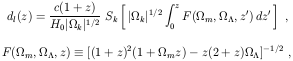
 x,
S+1
x,
S+1  sin and
S-1
sin and
S-1  sinh.
At z ~ 0.4, dl happens to be (to a good approximation)
a function of the combination
sinh.
At z ~ 0.4, dl happens to be (to a good approximation)
a function of the combination
 m -
m -

 (not q0)
[3].
The angular diameter distance, which enters the tests based on number density,
is simply
da = dl/(1 + z)2.
(not q0)
[3].
The angular diameter distance, which enters the tests based on number density,
is simply
da = dl/(1 + z)2.
 m and
m and

 within a few years,
once several supernovae are measured at z ~ 1
[4].
within a few years,
once several supernovae are measured at z ~ 1
[4].
 Measurements of the galaxy number count N(m, z)
seem to be in reach for surveys at high redshift
[5].
Measurements of the galaxy number count N(m, z)
seem to be in reach for surveys at high redshift
[5].
 The galaxy-type ``standard candles'' that were used over the years
clearly suffer from severe evolution complications.
Supernovae type Ia are the popular current candidate for a standard
candle, based on the assumption that
stellar processes are not likely to vary much in time.
The galaxy-type ``standard candles'' that were used over the years
clearly suffer from severe evolution complications.
Supernovae type Ia are the popular current candidate for a standard
candle, based on the assumption that
stellar processes are not likely to vary much in time.
 Systematic searches for supernovae are in progress.
Systematic searches for supernovae are in progress.
 Luminosity density distributions also have to assume
how galaxies evolve. If galaxies are formed in a series of hierarchical
mergers that continues at low levels today, there will be more galaxies
in the past than now, requiring an accurate theory of galaxy merging to
deduce an accurate estimate of density evolution linked to cosmology.
Luminosity density distributions also have to assume
how galaxies evolve. If galaxies are formed in a series of hierarchical
mergers that continues at low levels today, there will be more galaxies
in the past than now, requiring an accurate theory of galaxy merging to
deduce an accurate estimate of density evolution linked to cosmology.
 m -
m -

 < 2.5 as the 90%
two-parameter
likelihood contour (Fig. 1).
For a flat universe they find for each parameter
< 2.5 as the 90%
two-parameter
likelihood contour (Fig. 1).
For a flat universe they find for each parameter
 m =
0.94+0.34-0.28, and
m =
0.94+0.34-0.28, and

 < 0.51 (or
< 0.51 (or
 m > 0.49) at 95%
confidence. Improved results are expected soon from tens of supernovae.
m > 0.49) at 95%
confidence. Improved results are expected soon from tens of supernovae.
 So far, the galaxy number counts from the Hubble Space Telescope (HST)
and the 10-meter Keck telescope still yield conflicting results
(see a summary in
[6]).
So far, the galaxy number counts from the Hubble Space Telescope (HST)
and the 10-meter Keck telescope still yield conflicting results
(see a summary in
[6]).