


2.3. Number Count of Quasar Lensing
This is a promising new version of the classical number density test.
Strong sensitivity to

 arises when
arises when

 is positive and comparable
to
is positive and comparable
to  m. In this case,
the universe should have
gone through a phase of slower expansion in the recent cosmological
past, which should be observed as an accumulation of objects at a specific
redshift of order unity.
In particular, it should be reflected in the observed
rate of lensing of high-redshift quasars by foreground galaxies
[7].
The probability of lensing of a source at redshift zs
by a population of isothermal spheres of constant comoving density
as a function of the cosmological parameters is
[1]:
m. In this case,
the universe should have
gone through a phase of slower expansion in the recent cosmological
past, which should be observed as an accumulation of objects at a specific
redshift of order unity.
In particular, it should be reflected in the observed
rate of lensing of high-redshift quasars by foreground galaxies
[7].
The probability of lensing of a source at redshift zs
by a population of isothermal spheres of constant comoving density
as a function of the cosmological parameters is
[1]:
where
da(z1, z2) is the
angular diameter distance from z1 to
z2.
The contours of constant lensing probability in the
Pro:
This test shares all the advantages of direct geometrical measures,
e.g., being
independent of dark matter, fluctuations, GI and galaxy biasing.
The high redshifts involved bring about a unique sensitivity to
Con:
The constraint is weakened if the
lensed images are obscured by dust in the early-type galaxies
that are responsible for the lensing, especially
if E galaxies at z ~ 1 have nuch more dust than low-redshift ones
[8].
There is no clear evidence for a strong effect.
Current Results: From
the failure to detect the accumulation of lenses, the current limit for a
flat model is
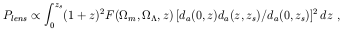
 m -
m -

 plane
for zs ~ 2
[1]
happen to almost coincide with the lines
plane
for zs ~ 2
[1]
happen to almost coincide with the lines
 m -
m -

 = const.
The limits from lensing are thus similar in nature to the limits
from SNIa.
= const.
The limits from lensing are thus similar in nature to the limits
from SNIa.

 ,
compared to the negligible effect that
,
compared to the negligible effect that

 has on the structure
observed at z << 1.
has on the structure
observed at z << 1.
 A similar uncertainty arises
if these galaxies had rapid evolution between
z ~ 1 and the present; current evidence suggests a weak evolution.
A similar uncertainty arises
if these galaxies had rapid evolution between
z ~ 1 and the present; current evidence suggests a weak evolution.
 The method was criticized for it's sensitivity
to the velocity dispersion assumed for the typical lenses and thus to the
galaxy luminosity function
[9],
but the requirement that the
distribution of lenses should simultaneously produce the observed
distribution of image separations largely
invalidates this criticism
[10].
The method was criticized for it's sensitivity
to the velocity dispersion assumed for the typical lenses and thus to the
galaxy luminosity function
[9],
but the requirement that the
distribution of lenses should simultaneously produce the observed
distribution of image separations largely
invalidates this criticism
[10].

 < 0.66 (or
< 0.66 (or
 m > 0.36)
at 95% confidence
[10]
(Fig. 1).
If
m > 0.36)
at 95% confidence
[10]
(Fig. 1).
If

 = 0, this test provides
only a weaker bound,
= 0, this test provides
only a weaker bound,
 m > 0.2
at 90% confidence. Several new lenses are found each year, promising slow
but continuous improvement.
m > 0.2
at 90% confidence. Several new lenses are found each year, promising slow
but continuous improvement.