The constitutive microscopic physics which determines the internal structure of globular cluster stars near the main sequence turnoff is contained in the nuclear energy processes, the opacities and the equation of state. The macroscopic physics, particularly the internal dynamics of star, present additional problems, most of which are not fully resolved, and are the subject of active research. The treatment of convection in the convective envelope is a source of uncertainty in calculating the model radius. Since a knowledge of the evolution of the stellar radius as a function of time is essential in fixing the position of the main sequence turnoff in the CMD for a given age, knowing the depth of the convection zone in turnoff stars is essential for age determinations. Internal rotation, particularly its effect on the composition profile through mixing due to circulation current or to rotationally induced turbulence, must be considered because it could modify the rate evolution and the shape of the evolutionary track near the turnoff as well, and trace element abundances reflect the extent of internal mixing which has taken place in the star. Rotationally induced turbulence interacts with diffusion (usually, but not always, against). Finally, the role of helioseismology in testing internal structure in a sensitive and discriminating way is discussed briefly. The next sections briefly highlight recent advances in each area, and the main topics of current investigation.
The nuclear energy generation rates relevant to low mass stars like the Sun and stars in globular clusters are rather well-known (Bahcall 1989; Bahcall & Pinsonneault 1992). There are still some uncertain reaction rates primarily of concern in the solar neutrino problem. Uncertainties in the reaction rates in the proton-proton chain and the CNO bicycle were included in the Monte Carlo simulation described in Section 5. It turns out that the principal source of age uncertainty relating to the energy generation is the uncertainty in the CNO abundance, particularly in the most abundant element oxygen, characterized by the [Fe/H] and [O/Fe] ratios.
The last few years have seen extraordinary advances in the calculation of stellar interior opacities. Particularly significant is the remarkable agreement between two independent sets of opacities derived using different physical modeling approaches, i.e. the opacities from the Opacity Project, led by M. Seaton and with the collaboration of D. Mihalas and other researchers, and the Livermore OPAL opacities (Rogers & Iglesias 1994; Iglesias & Rogers 1996). Helioseismology shows that solar models based on the OPAL opacities are much improved over previous generation solar models (Guenther et al. 1992). And OPAL opacities have resolved several long standing problems in stellar structure (e.g. the Cepheid and RR Lyrae mass discrepancy; the pulsation of subdwarf B stars), some of which are discussed in a review paper by Rogers and Iglesias (1994).
We note that, as expected, the difference between the earlier Los Alamos Opacity Library (LAOL) opacities (Huebuer et al. 1977) and the OPAL opacities is much less marked for low metallicities than for the solar metallicity (less than 2% in the interior of globular cluster stars). This is a reflection of the fact that hydrogen and helium dominate the opacities in low metallicity stars; as a result, the temperature structure in the core of globular cluster stars is less uncertain than in sun-like stars.
Important progress was also made in the calculation of low temperature opacities which must include molecules (Kurucz 1992). Several other independent tabulations of low temperature opacities have been published (Cox 1990; Carson & Sharp 1991; Neuforge 1994). The differences are of the order of 30% for the solar composition, and much less at low metallicities.
The corrections to the equation of state due to Coulomb interactions have recently been included (Debye-Hückel corrections) and are significant. The OPAL equation of state (Rogers et al. 1996) is responsible for a dramatic improvement in calculated solar p-mode frequencies, which now agree with observation to much better than 1% (Guenther et al. 1996). In the deep solar interior, the two formulations (D-H and OPAL) are very close. The two formulations affect metal poor isochrones in a nearly identical way, resulting in a decrease in globular cluster ages of 7% (Chaboyer & Kim 1995).
The efficiency of convection in the transition layer between the deep
adiabatic layers
and the primarily radiative atmosphere is poorly known, and is usually
described by the mixing length theory
(Böhm-Vitense
1958).
The free mixing length parameter, usually
defined as the ratio 
of the
mixing length to the local pressure scale height, can be
adjusted in the sun to fit the observed solar radius. The correct value
of to use
in isochrone construction is unknown, although using the solar
calibration works rather
well when new generation opacities are used in atmospheric layers. The
isochrones shown
in Figure 6, constructed with a constant value
of illustrate this
point. Nevertheless,
convection is the weakest link in the theory of isochrones; realistic 3D
simulations of the
convective-radiative outer layer of the Sun are now possible, and more
calculations of this kind are needed to replace the mixing length formalism
(Kim et al. 1995,
1996)
|
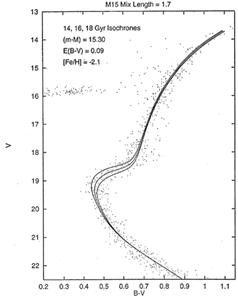
Figure 6. Isochrones constructed with a constant mixing length parameter of 1.7, superimposed on the CMD of M15. |
The rotational history of halo stars has been considered by Deliyannis et al. (1989), who included in their models the mixing due to rotationally induced turbulence and the associated transfer of angular momentum from the interior during evolution, following the precepts of Endal & Sofia (1978; 1981) and Pinsonneault et al. (1989). Although this rotational mixing has a significant effect on the mixing and depletion of Li at the surface of these stars, the rate of luminosity and radius evolution was practically unperturbed by the presence of rotation. This point is illustrated in Figures 7a and 7b.
|
Figure 7. (a) Comparison of pre-main sequence and turnoff evolution in the theoretic al HR-diagram for standard and rotating models. The standard and rotating sequences are practically indistinguishable. |
|
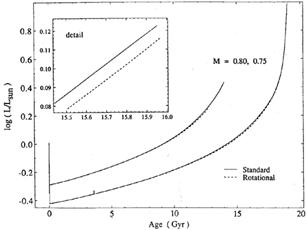
Figure 7. (b) The same evolutionary sequences as in Figure 7a, displaying the evolution of luminosity with time. As in Figure 7a, the standard and rotating sequences are indisguishable (from the work of Deliyannis et al. 1989). |
Because low metallicity stars have a more shallow convection zone than solar metallicity stars of the same effective temperature, helium diffusion is expected to be more efficient in these stars. Helium diffusion is thus expected to drain helium efficiently from the convection zones of globular cluster stars near the turnoff. Because the depletion of helium makes the stellar envelope expand, it modifies the position of the turnoff on an isochrone; for a given age, the turnoff is redder and fainter, all else being equal, as shown in Figure 8. This correction could lead to a substantial age reduction for globular clusters (Noerdlinger 1977; Stringfellow et al. 1983; Proffitt & Michaud 1991; Chaboyer et al. 1992). However, diffusion is inhibited by rotationally induced turbulence (Chaboyer & Demarque 1994), and its efficiency can be calibrated in halo stars by observations of the flatness of the Li plateau (Deliyannis & Demarque 1991; Pinsonneault et al. 1992); and in the Sun, by helioseismic tests (Guenther et al. 1996).
|
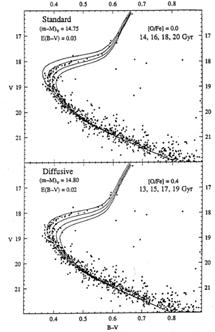
Figure 8. Effect of helium diffusion on isochrones in the CMD (from the work of Chaboyer et al. 1992). |
4.7. The impact of helioseismology
The advent of helioseismology has resulted in remarkable advances in our knowledge of the hydrostatic structure of the solar interior. The benefits and stimulating influence of helioseismology on our understanding of opacities and the equation of state in the solar interior permeate this discussion of the globular cluster ages. This influence extends not only to the deep interior by providing the means to date the Sun directly from the small p-mode spacings (Guenther et al. 1996), but also to the subphotospheric layers which are superadiabatic, and whose structure determines the specific entropy of the convection zone, and therefore the stellar radius (Demarque et al. 1997). Helioseismology, and soon asteroseismology thus hold the key to future progress in understanding the interior of the turnoff and subgiant stars used in dating star clusters.