


This section summarizes the results of a recently completed detailed
numerical study
designed to put a firmer bounds on the age and on the uncertainty in age
of the oldest
globular clusters in the Galaxy. The discussion consists of two
parts. In the first part,
1000 Monte Carlo realizations of stellar isochrones, based on estimates
of the range and
distribution of input parameters in the stellar evolution code, were
produced, which were
then used to derive the ages of the 17 oldest globular clusters. The
evolutionary tracks
were computed using the Yale stellar evolution code, and were
constructed using the same physical assumptions as in
Guenther et
al. (1992), and
Chaboyer & Kim (1995),
with a few relevant updates in the equation of state and the
[ / Fe] element ratio
discussed in
the previous section. These updates are not trivial when it comes to age
determinations,
as they altogether account for a reduction of as much as 17% of the
median maximum age over the
Chaboyer et
al. (1996a)
age scale (shown in Figure 2).
Then, incorporating estimates of the observational uncertainties in the
measured color-magnitude diagrams
and in the fitting procedure to the theoretical isochrones, a
probability distribution for
the mean age of the 17 oldest clusters was derived. The ages were
derived using a semi-empirical
/ Fe] element ratio
discussed in
the previous section. These updates are not trivial when it comes to age
determinations,
as they altogether account for a reduction of as much as 17% of the
median maximum age over the
Chaboyer et
al. (1996a)
age scale (shown in Figure 2).
Then, incorporating estimates of the observational uncertainties in the
measured color-magnitude diagrams
and in the fitting procedure to the theoretical isochrones, a
probability distribution for
the mean age of the 17 oldest clusters was derived. The ages were
derived using a semi-empirical
 V technique, in which the
absolute calibration was based on the empirical
absolute magnitude of the RR Lyrae variables
Mv(RR) = 0.6 ± 0.08 (rather than a purely
theoretical calibration)
(Layden et al. 1994).
The abundance of the
V technique, in which the
absolute calibration was based on the empirical
absolute magnitude of the RR Lyrae variables
Mv(RR) = 0.6 ± 0.08 (rather than a purely
theoretical calibration)
(Layden et al. 1994).
The abundance of the
 -elements was taken
to be [
-elements was taken
to be [ /Fe] = 0.55
± 0.05 (Gaussian) ± 0.2 (top- hat)
(King 1993;
Nissen et al. 1994).
Two totally independent color calibration tables of
Green et
al. (1987) and
Kurucz (1992)
were used.
/Fe] = 0.55
± 0.05 (Gaussian) ± 0.2 (top- hat)
(King 1993;
Nissen et al. 1994).
Two totally independent color calibration tables of
Green et
al. (1987) and
Kurucz (1992)
were used.
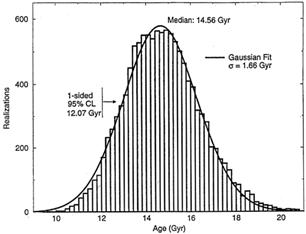
The age distribution for the oldest globular clusters is plotted in Figure 9. We see that the median age of the distribution is 14.56 Gyr, with a one-sided 95% Confidence Limit lower bound occurring at an age of 12.07 Gyr.
|
Figure 9. Histogram showing the relative number of realizations of mean cluster ages drawn randomly from the Monte Carlo data set using Mv(RR) = 0.6 ± 0.08, chosen from a Gaussian distribution. The dashed curve is a Gaussian approximation to the actual distribution (from the work of Chaboyer et al. 1996b). |
The reader is referred to the original paper for details in the input
parameters and
error estimates beyond what is discussed in
Section 4
(Chaboyer et
al. 1996b).
The Monte Carlo analysis yields quantitative estimates of the main
sources of uncertainties in
globular cluster ages. These uncertainties are listed in
Table 1. The Monte Carlo result
is consistent with former discussions of the problem of globular cluster
ages in identifying
the distance estimate (in this discussion the adopted
Mv(RR)), as the largest source of
age uncertainty (e.g.
Renzini 1991).
Other major uncertainties include the uncertainty in the CNO abundance (or the
[ /Fe] ratio), and the
choice of mixing length in the
convection zone. This last uncertainty, usually ignored in the past
primarily because of its intractability, is, as explained in
Section 4, one that needs to be explored more
fully. This is because the Monte Carlo realizations, while varying the
value of the mixing
length parameter from realization to realization, assume that this parameter
remains constant during evolution. Further work will need to explore the
possibility of
a distortion to the shape of evolutionary turnoff due to possible
variations in effective
mixing length as a star evolves. However, the Monte Carlo data also show
that unless
we find that convection behaves in a grossly unexpected way at low
metallicities near
the turnoff, the errors on the ages is likely to amount to only a few
percent in either
direction. We must conclude from this study that to the best of our
knowledge, the mean
age of the oldest globular clusters is 14.6 Gyr, with a 5% probability
that it is below 12.1 Gyr or above 17.1 Gyr. And that the probability
that globular clusters have the
same age as the oldest disk stars (i.e. 10 Gyr), is vanishingly
small.
/Fe] ratio), and the
choice of mixing length in the
convection zone. This last uncertainty, usually ignored in the past
primarily because of its intractability, is, as explained in
Section 4, one that needs to be explored more
fully. This is because the Monte Carlo realizations, while varying the
value of the mixing
length parameter from realization to realization, assume that this parameter
remains constant during evolution. Further work will need to explore the
possibility of
a distortion to the shape of evolutionary turnoff due to possible
variations in effective
mixing length as a star evolves. However, the Monte Carlo data also show
that unless
we find that convection behaves in a grossly unexpected way at low
metallicities near
the turnoff, the errors on the ages is likely to amount to only a few
percent in either
direction. We must conclude from this study that to the best of our
knowledge, the mean
age of the oldest globular clusters is 14.6 Gyr, with a 5% probability
that it is below 12.1 Gyr or above 17.1 Gyr. And that the probability
that globular clusters have the
same age as the oldest disk stars (i.e. 10 Gyr), is vanishingly
small.
| Error (±%) | |
| Mv(RR)(distance) | 16 |
[ /Fe] /Fe] | 7 |
| Treatment of convection | 5 |
| Helium diffusion | 4 |
| 1415N(p, y) O rate | 3 |
| Color transformation | 3 |