One of the major problems in comparing models to the observed luminosity function (LF) is that galaxy surveys are limited by the brightness of the night sky and by the desire to distinguish stars from galaxies. This imposes limits on the detectability of both high and low surface-brightness galaxies (Sect. 2.2.2). The standard assertion that a survey is ``magnitude limited'' assumes (1) that the isophotal threshold of the survey encompasses most of the light of all types of galaxies, and (2) that star-galaxy separation is not a problem. Neither assumption is safe for dwarf galaxies.
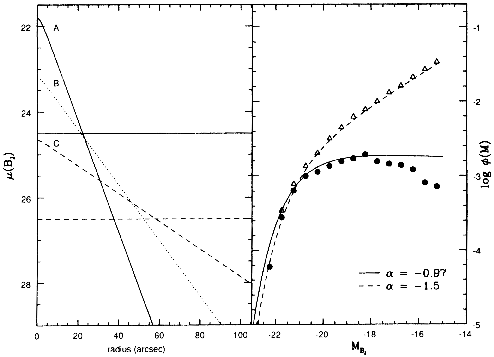
Figure 7. Illustration of the effect of isophotal selection and isophotal magnitude estimates on the field-galaxy luminosity function. The left panel shows simulated radial surface-brightness profiles for three exponential galaxies. Galaxy A has the canonical Freeman central surface brightness µ0 (BJ) = 21.6. Galaxies B and C have scale lengths a factor of 2 and 4 larger, respectively. The horizontal line shows the typical Automatic Plate Measuring (APM) machine isophotal threshold (Loveday et al. 1992). Galaxy C would be missed entirely by the survey, while galaxy B would have a measured ``total'' magnitude too faint by 0.7 mag, if the constant isophotal-to-total magnitude correction were based on galaxy A. The horizontal dashed line shows the isophotal threshold for the Fornax cluster survey (Ferguson 1989). The right panel shows a simulated field galaxy sample made up of exponential-profile galaxies with a steep intrinsic surface-brightness-luminosity relation and a luminosity function with M*BJ = -21,  = -1.5 in the
BJ band (see text). If galaxies could be detected
independent of surface brightness and their true total magnitudes
measured, the intrinsic luminosity function would be recovered (open
triangles). However, a survey that selects galaxies only above an
isophotal threshold of µ = 24.5, and adopts magnitudes based
on a constant isophotal-to-total magnitude correction (mtotal
= miso -0.27 assumed here), would recover the luminosity
function shown by the solid circles, similar to that observed by
Loveday et
al. (1992).
Further details of such simulations can be found in
Ferguson and
McGaugh (1994).
|
Figure 7 illustrates the importance of the isophotal
threshold. Shown at left are surface-brightness profiles for three
galaxies with the same total magnitude, but with different scale lengths.
Two isophotal thresholds are shown: the fainter one corresponding
to the
Ferguson (1989)
Fornax cluster survey, and the brighter
one corresponding to the APM surveys of Davies et al.(1987) for
the Fornax cluster and
Loveday et
al. (1992)
for the field.
For the right panel of the figure, imagine that the intrinsic field galaxy LF
is described by a Schechter function with MB* = -21
and = -1.5.
Imagine also that the faint end is dominated by galaxies that have
exponential profiles (Sect. 2.2.1)
and obey the following relation between central surface-brightness and
luminosity:
(This is basically a constant size relation with some scatter,
chosen to be illustrative rather than to reflect reality.)
The right panel shows the intrinsic LF and the LF recovered by a
field-galaxy survey similar to that of
Loveday et
al. (1992).
The recovered shape is significantly flatter than the intrinsic
slope both because many galaxies fall below the isophotal threshold,
and because the constant correction from isophotal to total magnitudes
systematically underestimates the flux from the galaxies with the
lowest surface brightnesses
(McGaugh 1994;
Ferguson and
McGaugh 1994).
While such surface-brightness dependent selection effects are important,
we will argue below that they are probably not sufficient to account
for the observed differences between the cluster and field LF's.
For clusters, an additional, equally important assumption
is that cluster members can be separated from interlopers, either
statistically or through redshift or morphological criteria.
As galaxy counts at faint magnitudes rise steeply
(log N(m)
where N is the number of galaxies in the field, and
The corollary is that if morphological selection does not
identify the full population of dwarfs in places like the Virgo
cluster (e.g. if there are many compact dwarfs that look just like
background galaxies or many LSB dwarfs below the thresholds of
photographic surveys), then the luminosity function could be
steeper than currently thought.
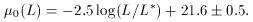
0.6
m), improper background correction can
seriously affect the estimate of in cluster samples.
For nearby clusters, where the increased
surface density of galaxies is not very high, statistical comparison of
counts in cluster fields to ``control'' fields is not very useful. If
the angular correlation function is a power law w(
) = A 1-
, then the variance in galaxy counts in a
square field of degrees on a side is
1.8
(Peebles 1975).
Consider the case at B = 20. Counts are about
200 mag-1 deg-2, and A 2 x
10-2
(Roche et al. 1993).
Over a 6° x 6° field, the variance is 
N2 = 5.6 x
105, meaning that random 6° x 6° patches of the sky will
show an RMS fluctuation of
N = 750 galaxies at B = 20. For
comparison, the morphologically-selected Virgo cluster catalog
(Binggeli et
al. 1985)
has only 112 cluster members with 19 < B <
20 in a field of roughly the same area. Because redshifts are very difficult
to obtain for such low-surface-brightness dwarfs,
morphological selection is currently the only way to obtain the
galaxy luminosity function to faint absolute magnitudes.