


Roughly 2000 dE's have been visually classified (from fine-scale photographic plates) on the Sandage and Binggeli (1984) system. Digitized photographic profiles have been measured for a small (~ 300), not necessarily random, subset of these (Ichikawa et al. 1986; Binggeli et al. 1984; Binggeli and Cameron 1991). Published CCD photometry exists for a still smaller (~ 100), still less random, subset (e.g. Caldwell and Bothun 1987; Impey et al. 1988; Bothun et al. 1991; Vader and Chaboyer 1994). Our knowledge of the quantitative photometric properties of these galaxies is thus still in its infancy.
The isophotes of dE's are typically well fit by ellipses. Analysis of the two-dimensional structure of the isphotes gives information on the intrinsic shapes of the galaxies (Sect. 2.2.3). The one-dimensional profiles (typically referred to the major axis, or to some mean axis) presumably also hold clues to how the galaxies collapsed and formed stars, and are the subject of the next section.
2.2.1
Surface-Brightness Profiles
The first dE profiles to appear in the literature were those of the six classical ``dwarf spheroidals'' derived by Hodge from star counts (see Hodge 1971 for detailed references). The pioneering work of Hodge has only recently been confirmed and superseded in accuracy by Irwin and Hatzidimitriou (1993). Hodge realized at once that neither Hubble's r-2 law (Reynolds 1913; Hubble 1930), nor de Vaucouleurs' (1948) law (I (r) = I0 exp (-7.67 (r / re)1/4) for giant ellipticals adequately describe the dwarf profiles. These looked almost box-like, i.e. flat in the inner part, followed by a sharp cut-off. A cut-off (``tidal'') radius had earlier been introduced by King (1962) for star clusters, and this seemed to apply to the dwarfs as well. Perfect fits to the ``spheroidal'' profiles were finally achieved by Hodge and Michie (1969) by employing the multi-parameter model of Michie (1963), which also allowed a dynamical interpretation. However, in later times the simpler King (1966) model has taken over for the purpose of profile fitting (it is a special case of the Michie model, cf. Binney and Tremaine 1987).
Strangely (as it appears in retrospect), only in 1983 was it appreciated (Faber and Lin 1983) that the profiles of ``dwarf spheroidals'' are fairly good exponentials (I (r) = I0 exp (-r / r0), where I0 is the central intensity and r0 is the scale length) - just as those of irregulars and of the disk components of spirals and S0's are (e.g. de Vaucouleurs 1959; Freeman 1970; Carignan 1985; Bothun et al. 1986). Not all of them are nice exponentials (e.g., the Draco system), which must be the reason why the exponential was dismissed by Hodge, but such deviations are also common among irregular profiles. Better fits can always be achieved with 3-parameter forms like Oemler's (1976) modified Hubble law (Caldwell 1983; Binggeli et al. 1984), or King profiles (Binggeli et al. 1984; Ichikawa et al. 1986; Ichikawa 1989; Binggeli and Cameron 1991; Vader and Chaboyer 1994). However, the exponential is more economical with only 2 free parameters (central surface brightness and scale length) and it is almost universal for faint galaxies, allowing easy comparison of photometric parameters between different types of dwarfs. For a comparison with normal ellipticals, the King profile is still useful, because it applies to E's as well as dE's (see below).
Following Faber and Lin (1983), it was quickly shown that the exponential is also a good fitting law for Virgo cluster dwarf ellipticals (Binggeli et al. 1984), leading to the notion that there are two separate families of elliptical-like galaxies: diffuse dwarf ellipticals (``spheroidals'') that have nearly exponential profiles versus classical ellipticals (including M32) that follow a de Vaucouleurs r1/4 law (Wirth and Gallagher 1984). The structural similarity between dwarf irregulars and dwarf ellipticals also reopened the discussion, pioneered by Einasto et al. (1974), on a possible evolutionary Irr -> dE transition (Lin and Faber 1983; Kormendy 1985; Binggeli 1986; Bothun et al. 1985; Bothun et al. 1986; cf. Sect. 7.6 for the later development).
In spite of the current popularity of the exponential as a fitting law
for dE profiles, it is important to note that only faint dE's
(MB > -16, the majority, to be sure) are good exponentials
everywhere, i.e. over the whole radius range. Bright dE's
(MB  -16) usually
deviate from an exponential in their inner
part; there is a central surface brightness excess which, on average,
is stronger in brighter galaxies
(Caldwell and
Bothun 1987;
Binggeli and
Cameron 1991).
Binggeli and
Cameron (1991)
have introduced profile types for early-type galaxies based on the
degree of linearity of the profile.
Caldwell and
Bothun (1987)
identify the central light excess in a
bright dE, i.e. the residual from the exponential fit to the outer part,
as ``the nucleus''. However
Binggeli and
Cameron (1991)
contend that there are two components to the central excess: one that
is currently unresolved at Virgo distances, and the other extended
over several arcsec. In most bright dwarfs one can clearly see such a sharp
nucleus on top of a shallow, extended surface brightness excess.
Faint dE's, on the other hand, frequently have nuclei, but rarely
show the more extended excess.
The distinctness and non-resolution (point-source nature) of some very
bright dE nuclei is illustrated in
Fig. 2, seen in this
case on top of King, rather than exponential, profiles.
-16) usually
deviate from an exponential in their inner
part; there is a central surface brightness excess which, on average,
is stronger in brighter galaxies
(Caldwell and
Bothun 1987;
Binggeli and
Cameron 1991).
Binggeli and
Cameron (1991)
have introduced profile types for early-type galaxies based on the
degree of linearity of the profile.
Caldwell and
Bothun (1987)
identify the central light excess in a
bright dE, i.e. the residual from the exponential fit to the outer part,
as ``the nucleus''. However
Binggeli and
Cameron (1991)
contend that there are two components to the central excess: one that
is currently unresolved at Virgo distances, and the other extended
over several arcsec. In most bright dwarfs one can clearly see such a sharp
nucleus on top of a shallow, extended surface brightness excess.
Faint dE's, on the other hand, frequently have nuclei, but rarely
show the more extended excess.
The distinctness and non-resolution (point-source nature) of some very
bright dE nuclei is illustrated in
Fig. 2, seen in this
case on top of King, rather than exponential, profiles.
The profiles of the very brightest dE's and dS0's are almost as strongly curved as the profiles of normal ellipticals. Binggeli and Cameron (1991) attempt a separation between E's and dE's by going to the logarithmic (log r) representation of profiles, and by fitting King (1966) models to both E's and dE's. In the radius range 0.1 to 1 Kpc, the profiles of early-type galaxies appear to fall into two distinct classes: (1) the steep profiles of ``normal'' (or ``classical'') ellipticals and S0's, and (2) the significantly flatter profiles of ``dwarf'' ellipticals and S0's (called so by definition). The latter group includes all the ``intermediate'' (E/dE) cases, as judged from morphology. In terms of best-fitting King model profiles, the normal/dwarf ellipticals have high/low central surface brightnesses and small/large core radii, again supporting the notion of a dichotomy among elliptical stellar systems. However, the King model does not fit the bright dwarf profiles very well. As with the exponential fits, there remains a strong, extended surface brightness excess in the central part, which casts some doubt on the whole fitting procedure. When the central excess is ignored, the dichotomy between dE and E galaxies is pronounced. However, it is not clear that a strong dichotomy remains when model-independent central-surface brightnesses are used. Binggeli and Cameron (1991) were not able to resolve any of the low-luminosity (M32-type) ellipticals in their sample (``resolve'' in the sense of Schweizer 1979; 1981); they could only surmise that these would be nearly as compact as M32. Prugniel et al. (1992) claimed resolution of the very same compact E's and reported a continuity of profiles between E's and dE's. However, Kormendy and Bender (1994), working with the superior resolving powers of CFHT and HST, make clear that the cores of those compact galaxies are yet to be resolved. It is thus still not clear whether E's and dE's form distinct sequences in their core parameters. In any case, the number of objects in this E/dE intermediate zone is very small (Prugniel 1994; Vader and Chaboyer 1994).
2.2.2
Parameter Correlations and Selection
Effects
In photometric diagrams involving the model-independent
effective parameters re
and < µ >e, the mean surface brightness within
re, early-type galaxies are confined to one
broad sequence with a distinct, almost orthogonal break around
MB  -20,
< µ >e
-20,
< µ >e  21 B mag per square arcsec,
and log re [kpc]
21 B mag per square arcsec,
and log re [kpc]  0.3
(Kodaira et
al. 1983;
Binggeli et
al. 1984;
Binggeli and
Cameron 1991;
Capaccioli et
al. 1993).
Galaxies on the bright branch have increasing surface brightness with
decreasing luminosity (known since
Kormendy 1977),
while galaxies on the faint branch, i.e. the
dwarfs, follow the inverse trend, with a scaling law of
0.3
(Kodaira et
al. 1983;
Binggeli et
al. 1984;
Binggeli and
Cameron 1991;
Capaccioli et
al. 1993).
Galaxies on the bright branch have increasing surface brightness with
decreasing luminosity (known since
Kormendy 1977),
while galaxies on the faint branch, i.e. the
dwarfs, follow the inverse trend, with a scaling law of
for a Virgo cluster distance modulus of 31.7
(Binggeli and
Cameron 1991).
The scatter of this relation
is considerable (0.8 mag at the 1
In the King model representation of profiles, the dE sequence is
essentially delineated by the central surface brightness, with
µ0
In the exponential representation of the profiles, the best-fitting exponential
scale-lengths (r0)
and central surface brightnesses (µ0) of the dE's
follow the same
general trend; both are monotonically decreasing with decreasing luminosity.
However, there is a break around MB = -16 in the
r0 - M and
µ0 - M relations
(Binggeli and
Cameron 1991):
for bright dwarfs (MB < -16) the relations are
for faint dwarfs (MB > -16) we have
again for a Virgo modulus of 31.7. The near constancy
of µ0 of bright dwarfs is reminiscent of
``Freeman's law'' for spiral galaxies
(Freeman 1970;
van der Kruit 1987);
see also Fig. 3).
Binggeli and
Cameron (1991)
speculated that the inflection around
MB = -16
might reflect a transition from bright, rotation-supported stellar disks
to faint, pressure-supported spheroidals. There are indeed many dS0's among
the bright dwarfs, whose disk nature seems manifest. However, there are
hints that bright dE's are non-rotating as well
(Bender and Nieto
1990).
The location of dwarf ellipticals in the µ - M plane
identifies them as a distinct class of object.
Fig. 3, taken from
Binggeli (1994b),
shows a schematic µ - M
diagram for all kinds of stellar systems and subsystems (disks, bulges,
nuclei, star clusters). Here, µ is the model-independent,
apparent central surface brightness in the sense of
Kormendy (1985).
The two sequences of dE's
versus E's + bulges, and the problem of their connection (indicated by a
question mark) have been discussed above. A third sequence of purely stellar
systems, at low luminosities but high densities, is formed by globular
clusters. Galaxian nuclei probably belong to the same sequence and extend
it to higher densities and luminosities. The nuclei of M31
(Lauer et al. 1993)
and M33
(Kormendy and
McClure 1993),
as well as the nuclear magnitudes of
all dE,N's
(Binggeli and
Cameron 1991)
fall indeed into the region indicated.
A fourth sequence is defined by the disk components of spiral and S0 galaxies,
and dwarf irregular galaxies. At the bright end, this sequence levels off at
µ0(B)
The close kinship of the dE and S+Irr sequences is of course suggestive of a
common origin of the two classes of objects
and an evolutionary connection in the direction S+Irr
-> dE (e.g.,
Kormendy 1985,
1986).
However, bright dE's
(MB < -16) have systematically higher surface
brightness than disk galaxies of the same luminosity, which is one of
the reasons why a simple gas removal scenario does not work there
(Bothun et al. 1986;
Davies and
Phillipps 1988;
James 1991;
Binggeli 1994a;
cf. also Sect. 7.6). On the other hand,
faint dE's and Irr's (MB > -16) are often hard
to distinguish
with respect to morphology and even stellar content. There are many
``intermediate'' types of ``mixed morphology'' (cf. above).
However, environments such as the Virgo cluster are overwhelmingly
dominated (in number) by smooth-profile galaxies.
A separation into ``dwarf" and non-dwarf (``normal'', ``giant'', ``classical'')
types along the S+Irr sequence is not as clear-cut as it appears
between the E and dE sequences. A possible parallel definition
to the one for early-type dwarfs has been suggested by
Binggeli (1994a):
a late-type galaxy should be called ``dwarf'' if it lacks an E-like bulge.
This would include also many Sc spirals. The general definition for dwarf
galaxies would then be: dwarf galaxies have no E-component. There
are of course difficulties with such a definition (cf.
Binggeli 1994a,
b).
In any case (but certainly for M > -16 ), one can speak of a
common, broad
sequence of dwarf galaxies, which is indeed the main sequence of
galaxies.
There is a possible caveat. The photometric sequences in the
µ - M
plane might be shaped, if not produced, by selection effects. Both very
compact, high-surface brightness objects and extended, very low-surface
brightness objects have small isophotal diameters and can easily go
undetected in a survey. A photometric sequence could just be what is
visible within the detection limits.
Reaves (1956)
and Arp (1965)
issued the first warnings to this effect. The issue was
vigorously taken up and quantified by the Cardiff group led by M. Disney
(Disney 1976;
Disney 1980;
Disney & Phillipps
1983;
Disney & Phillipps
1987).
A great boost for the suspicion that entire
populations of galaxies are missing in our conventional catalogs was
provided by the serendipitous discovery of ``Malin 1'', a very huge,
very low-surface brightness spiral
(Bothun et al. 1987).
This object indeed
falls off any sequence (see Fig. 3). Additional very
low-surface brightness objects turned up in the Virgo
(Impey et al. 1988)
and Fornax
(Bothun et al. 1991)
clusters, obviously being cluster members. Earlier,
Sandage & Binggeli
(1984)
had found many brighter examples of this
class of ``huge, low-surface brightness dwarfs'' (cf. above). These
objects progressively broaden the µ - M sequence of
dwarf galaxies
towards the faint end (see Fig. 3), posing
severe problems for the determination of the faint end of the luminosity
function (Sect. 5).
The existence of any µ - M relation for dwarfs was denied
altogether by
Davies et
al. (1988) and
Phillipps et
al. (1988).
For dE galaxies in clusters, the argument hinges on whether faint,
relatively high surface-brightness objects are cluster members or
background galaxies
(Ferguson &
Sandage 1988;
Irwin et al. 1990a;
Bothun et al. 1991).
In deep surveys of the region of the Fornax cluster
(Ferguson &
Sandage 1988;
Ferguson 1989;
Bothun et al. 1991),
the surface-density enhancement of
the cluster is readily seen in the spatial distribution of classical
dE galaxies (those that lie on the µ - M relation),
while the cluster
is not at all visible in the spatial distribution of galaxies
that lie off the relation. However,
Irwin et al. (1990a)
see the number counts on the Fornax cluster UK Schmidt plate enhanced
at all surface-brightnesses relative to a nearby comparison
field. Furthermore,
Phillipps et
al. (1988)
show that field dwarf irregulars may not follow an intrinsic
surface-brightness luminosity relation.
Overall, it must be admitted that there are several regions in the
µ - M plane where we have a blind eye, i.e., where
the visibility of
objects is very low, and where more sequences of galaxian objects
might one day be uncovered. However, the surveys for (in particular)
low-surface brightness objects that have been undertaken so far suggest
that the extremes of the surface-brightness distribution are not
heavily populated. In the luminosity range well sampled by such surveys,
the ridge line dE sequence is well defined and is certainly
not an artifact of any detection limits, or visibility function
(even if the full extent of the scatter is not yet well quantified).
Hence the sequence
must be a physical reality, and must have a physical origin, which
is dealt with in Sect. 7.
Overall, dwarf ellipticals are slightly more flattened than normal E's
(Binggeli &
Popescu 1994;
Ryden & Terndrup
1994).
Previous studies
suffered from strong systematic errors in the eye-estimated flattening data.
Apparently round (ellipticity class E0) systems, among both E's (e.g.,
Binney & de
Vaucouleurs 1981) and dE's
(e.g.,
Sandage et
al. 1985a),
were grossly overabundant due to the tendency of the eye (mind) to see (force)
perfect symmetry where there is only near symmetry. Reliable (photometrically
measured) ellipticity distributions were determined for dE's
(Ichikawa et
al. 1986;
Ichikawa 1989)
even before the equivalent became available
for E's
(Franx et al. 1991;
Ryden 1992).
There is good agreement about the apparent ellipticity distribution of dE's,
except that
Binggeli & Popescu
(1994)
find that only the non-nucleated dE's
are significantly more flattened than the E's, while
Ryden & Terndrup
(1994)
claim the same effect for nucleated dwarfs as well. That the dE,N's tend to be
rounder than the dE(no N)'s has been noted before - without claiming
significance -
by van der Bergh
(1986),
Impey et al. (1988),
Ferguson & Sandage
(1989) and
Ichikawa (1989).
A dynamical explanation of the effect has been offered by
Norman (1986),
based on the work of
Norman et
al. (1985).
These authors have shown that a dense central cusp in the center of a triaxial
system with a substantial fraction of box orbits will, over many crossing
times, make the galaxy rounder. For a nucleated dwarf, a decrease of one or
two ellipticity classes over a Hubble time can be expected. However, whether
the nuclei have been around for a Hubble time must be questioned. There are
hints that some of the nuclei formed much more recently
(Davies & Phillips
1988;
Meurer et
al. 1992).
Alternatively, the more flattened dwarf systems,
due to higher (?) angular momentum, might have avoided substantial
infall of gas into their centers, thus preventing the formation of a nucleus.
The problem here is that flattening and angular momentum are not clearly
correlated: neither bright nor faint dE's appear to be rotation-supported
(Bender & Nieto 1990;
Bender et al. 1992).
The surface brightness test for the intrinsic shape of elliptical systems
(Marchant & Olson
1979;
Richstone 1979),
if taken at face value, clearly
favours the oblate over the prolate spheroid - for normal ellipticals (e.g.,
Fasano 1991,
and references therein) and dwarf ellipticals alike
(Ichikawa 1989;
Binggeli & Popescu
1994).
Both E's and dE's are more likely
triaxial in shape. The pure oblate model is barely able to reproduce the
paucity of apparently round E's
(Franx et
al. 1991) or dE's
(Binggeli &
Popescu 1994).
The flattening distributions of smooth dwarf irregulars (Im's) and of (at
least the) non-nucleated dE's are surprisingly similar
(Binggeli &
Popescu 1994),
confirming earlier findings by
Ichikawa et
al. (1986),
Feitzinger &
Galinsky (1986) and
Ferguson & Sandage
(1989),
however disproving the often cited result of
Sandage et
al. (1985a).
This supports the view that the non-nucleated dE's are the dead remnants
of formerly star-forming dwarf galaxies that, by internal or external causes,
lost or consumed their gas
(Davies &
Phillipps 1988;
Thuan 1992;
Binggeli 1993).
However, the fact that the nucleated dE's are rounder
than the late-type dwarfs does not, per se, exclude the possibility that they,
too, are such remnants. There are various ways for a star-forming disk to
puff up along its - presumably violent - transition into a purely stellar
system
(Biermann &
Shapiro 1979;
Farouki & Shapiro
1980;
Davies & Phillips
1988).
Therefore, the shapes of dwarf galaxies, and
of galaxies in general, do not provide very strong constraints on evolutionary
connections between the different types (cf. also
Sect. 7.6).
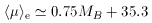
 level) but nevertheless allows
the use of µ as a distance indicator (see
Sect. 8.1).
The identification of the two branches with two fundamentally different
sequences of galaxies rests of course on the disparity, if not
dichotomy, of the profiles discussed above.
level) but nevertheless allows
the use of µ as a distance indicator (see
Sect. 8.1).
The identification of the two branches with two fundamentally different
sequences of galaxies rests of course on the disparity, if not
dichotomy, of the profiles discussed above.
 MB. The
core radius is roughly constant at rc
MB. The
core radius is roughly constant at rc
 1 kpc, albeit with much
scatter. The third parameter, the
concentration index log rt/ rc,
again tends to decrease
with decreasing luminosity, i.e. the cut-off length of the dwarfs gets
shorter and shorter
(Binggeli et
al. 1984;
Ichikawa et
al. 1986;
Binggeli and
Cameron 1991).
In the context of
King's (1966)
dynamical model, rt
has the meaning of a tidal radius. The observed log
rt/ rc - M relation is
plausible, qualitatively, because low-mass galaxies
will be more more easily and deeply stripped by tidal forces. The
problem is to find a tidal agent.
Binggeli et
al. (1984)
used the formulation of
Richstone (1976)
to calculate the cumulative tidal effect exerted on a
Virgo cluster dwarf galaxy by the frequent
encounters it has with other
cluster galaxies. The effect turned out to be quite small. Another
possibility was explored by Binggeli (unpublished) based on
Merritt's (1984)
model in which the size of cluster galaxies is determined by the
tidal field of the cluster as a whole. The dwarfs could indeed just
barely have been shaped by this process, which roughly also reproduces
the slope of the observed rt - M
relation. However, dE's outside clusters are, so far as we
can tell, indistinguishable from cluster dE's. Also, faint dE's are perfect
exponentials, just like the dwarf irregulars which cannot possibly be
interpreted as King spheroidals. Thus the ``tidal'' radius is probably an
intrinsic property of the dE's, and is probably not useful
as a diagnostic of tidal agents (e.g. for probing the
galactic halo as in
(Faber and Lin
1983).
1 kpc, albeit with much
scatter. The third parameter, the
concentration index log rt/ rc,
again tends to decrease
with decreasing luminosity, i.e. the cut-off length of the dwarfs gets
shorter and shorter
(Binggeli et
al. 1984;
Ichikawa et
al. 1986;
Binggeli and
Cameron 1991).
In the context of
King's (1966)
dynamical model, rt
has the meaning of a tidal radius. The observed log
rt/ rc - M relation is
plausible, qualitatively, because low-mass galaxies
will be more more easily and deeply stripped by tidal forces. The
problem is to find a tidal agent.
Binggeli et
al. (1984)
used the formulation of
Richstone (1976)
to calculate the cumulative tidal effect exerted on a
Virgo cluster dwarf galaxy by the frequent
encounters it has with other
cluster galaxies. The effect turned out to be quite small. Another
possibility was explored by Binggeli (unpublished) based on
Merritt's (1984)
model in which the size of cluster galaxies is determined by the
tidal field of the cluster as a whole. The dwarfs could indeed just
barely have been shaped by this process, which roughly also reproduces
the slope of the observed rt - M
relation. However, dE's outside clusters are, so far as we
can tell, indistinguishable from cluster dE's. Also, faint dE's are perfect
exponentials, just like the dwarf irregulars which cannot possibly be
interpreted as King spheroidals. Thus the ``tidal'' radius is probably an
intrinsic property of the dE's, and is probably not useful
as a diagnostic of tidal agents (e.g. for probing the
galactic halo as in
(Faber and Lin
1983).
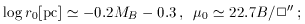
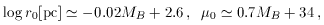
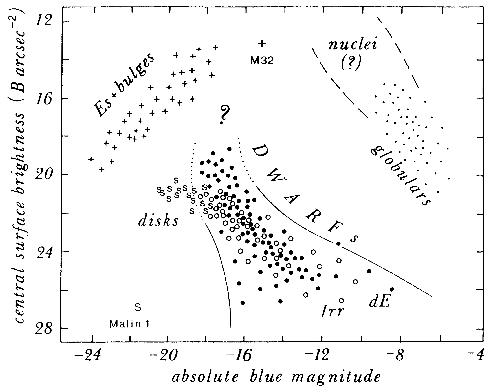
Figure 3. Schematic MB - µ plane
for stellar systems and subsystems. Dwarf ellipticals and dwarf
irregulars, for MB > -16, follow a common
MB - µ relation of normal E's and
bulges. For more details see text. Taken from
Binggeli (1994b).
 21
(Freeman 1970;
van der Kruit
1987).
Fainter than MB
21
(Freeman 1970;
van der Kruit
1987).
Fainter than MB  -17 or so, the central surface brightness
starts to get fainter and fainter with decreasing luminosity, i.e. the
sequence bends over to the µ - M relation of dwarf
irregulars, which is
identical to that of faint dE's, although clumpy irregulars (``BCD's'' -
not shown in the figure) tend to widen the distribution.
-17 or so, the central surface brightness
starts to get fainter and fainter with decreasing luminosity, i.e. the
sequence bends over to the µ - M relation of dwarf
irregulars, which is
identical to that of faint dE's, although clumpy irregulars (``BCD's'' -
not shown in the figure) tend to widen the distribution.
2.2.3
Flattenings