If the formation of galaxies depends on environment, then both the
fraction of mass in galaxies and the mass function of galaxies may
in the end vary over large scales. The concept of biased galaxy
formation emerged in the 1980's
(Kaiser 1984;
Rees 1985;
Davies et al. 1985;
Bardeen et
al. 1986)
as a way to reconcile the theoretically attractive ``flat universe''
with 
= 1 to the lower inferred from the virial
analysis of rich clusters and from studies of large-scale structure.
There are many plausible ways to introduce bias into the distribution
of galaxies
(Rees 1985;
Dekel 1986).
Spatial variations in the efficiency of galaxy formation could arise from
the nature of the dark matter (e.g. if a significant fraction of
is in hot neutrinos), from the existence of a universal threshold
in the density required for galaxy formation (see below), or from
the coupling of galaxy formation to the feedback of energy from the
first generations of objects (e.g. via photoionization of the IGM from
early starbursts or AGN, or via bulk flows introduced by early supernovae).
Because of the uncertainties in the physics, it has been convenient to
parametrize biasing by a single parameter b that is the ratio of
the rms density fluctuations in luminous matter to the underlying
rms mass fluctuations. Because ellipticals and spirals cluster differently,
the value of b obviously depends on galaxy type. The COBE results
suggest that b also depends on the scale over which the rms
fluctuations are measured
(Efstathiou et
al. 1992;
Padmanabhan and
Narasimha 1992),
at least for CDM-like power spectra.
Some type of biasing mechanism is clearly necessary to explain the
clustering properties of dE galaxies (Sect. 6).
Perhaps the most thoroughly developed is the concept of statistical
biasing, based on the idea that galaxies form above some global threshold
in the Gaussian random field of
primordial fluctuations
( = 
/ 
where is the rms density variation on a
given scale). A standard hypothesis
(Dekel and Silk 1986;
White et al. 1987;
Schaeffer and Silk
1988)
has been that giant
galaxies form only at 
2-3, while dwarfs can form
at any peak (and so the vast majority of them should come from
typical peaks of = 1). Such a model
predicts that giant galaxies
should be more correlated than dwarfs. The enhancement in the
giant-galaxy two-point correlation function 
g relative to the mass
two-point correlation function m is approximated by
(Kaiser 1984;
Politzer and Wise
1984)
which corresponds to roughly an order of magnitude at
West (1993)
has argued that the same sort of statistical bias may
account for different specific globular cluster frequencies of
spiral and elliptical galaxies, and the higher globular cluster
frequencies of cD galaxies. If one assumes that globular clusters
can only form at density peaks higher than some global critical value
As a mechanism for forming globular clusters, West's proposal faces
serious difficulties. For example, there is no evidence that globular
clusters have dark-matter halos, as they must in this model. Furthermore,
the CDM power spectrum, which produces the best match to the
trends in globular-cluster specific frequencies, would predict a
globular-cluster mass function steeply rising to low masses,
and extending to higher masses,
contrary to observation. Finally, it appears that at least some globular
clusters, for example the relatively young ones observed in
the LMC and
NGC 1275
(Holtzman et
al. 1992),
form at late epochs,
probably not through collapse onto primordial density fluctuations.
On the other hand, West's proposal is perhaps more attractive for explaining
the clustering of dE galaxies, which show strong evidence for dark matter
and have a steeply rising mass function (although not as steep as
CDM models predict). The idea that statistical bias could enhance
the clustering of dE galaxies
runs contrary to all previous statements about the influence
of statisical bias on the clustering properties of dwarf galaxies,
but nevertheless has the positive feature that it could potentially
account for the variation of the dwarf/giant ratio with cluster richness
(Sect. 6),
and it may provide a natural explanation for the high central
dark-matter densities inferred for some dwarf ellipticals
(Sect. 3).
However, interpretation of the clustering of dE galaxies in the context of
statistical biasing requires that their formation threshold
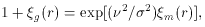
/ = 3.
Although an explicit estimate of g for dE galaxies has not been made,
the available data clearly rule out any appreciable decrease in g
from giant E's to dE's (see Sect. 6).
(The data are still ambiguous for the comparison of field Irr's to field
spirals -
(Eder et al. 1989;
Salzer et al. 1990;
Alimi 1994.)
, the enhancement in the globular
cluster frequency in galaxy
and cluster halos can be calculated from the formalism described above.
For reasonable choices of the power spectrum and the density thresholds
for spirals, ellipticals, and rich galaxy clusters, the observed
variation of the globular cluster specific frequency can be reproduced.
West (1993)
speculates that the same reasoning might apply to
dwarf galaxies, which for the same threshold ought then
to be more strongly clustered than globular clusters.
was comparable to that of giant
elliptical galaxies. The
condition that giant ellipticals form at high peaks
arises naturally from the standard cooling time argument:
the density of their halos must be
high enough that the cooling time will be shorter than the
free-fall time (Sect. 7.3). However, the
cooling time decreases
rapidly with decreasing halo velocity dispersion
(tcool 
V2),
so this mechanism cannot be invoked to argue for a high for
dE galaxies. While other possible mechanisms exist
(West 1993),
missing
from the argument is a compelling physical reason why dE's (or globular
clusters) should form only above some global density threshold.