Dwarf elliptical galaxies clearly once had gas and formed stars, and therefore must at some time in their past have looked like dwarf irregular galaxies. Could dE's simply be highly evolved irregulars? The secular evolution of irregulars to dE's, with evolutionary time scale being controlled by the environment, could plausibly account for the different clustering properties of dE and irregular galaxies (see Sect. 6). There are, in fact, many intermediate-type (dE/Irr) dwarf systems in the Virgo cluster and around massive field giants where we may be witnessing the conversion of an irregular to a dE (Sandage and Binggeli 1984; Vigroux et al. 1986; Sancisi et al. 1987; Sandage and Hoffmann 1991; Sandage and Fomalont 1993). In this section we review processes that could bring about such a conversion.
7.6.1. Sweeping
Gas will be stripped from a galaxy moving through a hot medium if the ram pressure exceeds the restoring force per unit area due to the galaxy's own gravity (Gunn and Gott 1972). For a spherical galaxy, ram pressure will be effective if
where
for a galaxy of radius r in a cluster of velocity dispersion
where rkpc is the galaxy radius in kpc,
which suggests a stripping timescale of 2 x 109 yr for
a galaxy with a mass in gas of M = 108
M
The above arguments suggest that in clusters such as Virgo, gas
removal will be relatively slow except in the central regions
of the cluster. Galaxies on orbits that do not pass through the
central ~ 0.5 Mpc will probably retain
gas for several times 109 years. Galaxies that orbit beyond
the central Mpc could retain their gas for a Hubble time.
Unless the orbits are predominantly radial, we should expect to
see a large variation in the gas content of dwarf galaxies over
the central few Mpc of the Virgo cluster. Observationally, dE's
are the dominant dwarf-galaxy population over this entire
region, and there are no obvious systematic variations in their
properties with position in the cluster,
other than the frequency of nucleation (Sect. 6).
We conclude, purely on the basis of these arguments, that stripping
was probably not the dominant gas-removal mechanism in environments
such as the Virgo and Fornax clusters.
A similar argument suggests
that stripping is probably not the major gas removal mechanism
for the Milky Way companions. For a galaxy of radius 1 kpc to
lose 2 x 107 M
However, these simple arguments neglect the fact that the
interstellar media of galaxies are multi-phase. Low-density
diffuse gas will be much more easily stripped than the high-density
gas that is directly associated with star formation. What effect
this has on the evolution of a galaxy therefore depends on how gas
circulates from dense to diffuse phases - a process that is stopped
by sweeping at densities much lower than required for removal of the
entire ISM. If sweeping by an external medium is the dominant
gas-removal mechanism (i.e. if all dE's pass through high density
regions at some time during their lives), the natural consequence
is that the metallicity-luminosity relation should not exist,
or should be modulated by environment. While the stripping timescale
depends on galaxy mass, leading to some correlation, it also depends
on galaxy orbit and the time when the galaxy encountered a
dense external medium, both of which are probably independent of
mass, but may introduce correlations of metallicity with position. No
such correlations have been identified, but they have not been
ruled out either.
Independent of this discussion, there are four classical
arguments against a pure stripping scenario for dE's brighter than about
MB = -14
(Davies and
Phillipps 1988;
Binggeli 1994a):
(1) bright dE's have nuclei and irregulars do
not, (2) bright dE's have surface brightnesses that are
too high compared to irregulars
(see Fig. 3), (3) bright Im's
are flatter than bright dE's,
(4) dE's are more metal-rich than Im's
(Zinnecker and
Cannon 1986;
Thuan 1985).
Of these, argument (3) now appears considerably weaker
(Sect. 2.2.3), and argument (2) has
not been demonstrated explicitly for complete samples, controlling for
the underlying luminosity-metallicity correlation.
Even if interaction with a surrounding medium does not remove all
the gas, it is possible that it influences the star
formation histories of dE galaxies in other ways.
Episodic encounters of dE's with
dense gas, either in galaxy halos or in clusters, could provide a
mechanism for forming multiple, distinct generations of stars, thus
enhancing surface brightness and metallicity, and for
forming the nuclei. In this regard, the effect of pressure
confinement by the external medium may be more important than the gas
removal processes discussed above.
7.6.2. Pressure confinement
Pressure confinement by the intracluster medium has been
considered by
Fabian et
al. (1980) and by
Babul and Rees
(1992)
in the context of dwarf galaxies. For a gas cloud of mean density
ng and temperature Tg to be in pressure
equilibrium with a surrounding medium of density nh
and temperature
Th, we require that ng
Tg
On the other hand,
White and Frenk
(1991) and
Cole et al. (1994)
argue that star formation will be self-regulated (see
Sect. 7.5.1),
with dwarf galaxies maintaining a large reservoir of gas at the
virial temperatures of their halos by injection of energy
from a roughly constant of star formation.
Interaction with the ICM will increase the
density, and hence shorten the cooling time of the gas.
Once the external pressure dominates, the cooling time
scales roughly as tcool
7.6.3. Tidal Shaking
Since cooling and star formation (presumably) depend on density,
in principle any mechanism that can perturb the density of
gas in a quiescent dwarf irregular can increase the star
formation rate. If gas is subsequently expelled either by
winds or stripping, the galaxy can complete its transition from
an irregular to a dE. One possible mechanism that does
not require an external gaseous medium is ``tidal shaking''
(Miller 1988).
Tidally induced star formation has been invoked
in the context of hierarchical models
(Lacey and Silk
1991;
Lacey et al. 1993),
where the details of the mechanism were not specified.
The process has never really been quantified for dwarfs. However,
Icke (1985)
carried out hydrodynamical simulations for
rotating disk galaxies that indicate that even distant encounters can
cause shocks in the ISM without significantly perturbing the stars.
The development of shocks
depends on the mass of the perturber and the mass ratio
of the perturber to the perturbed galaxy. Icke's scaling relations
imply that for a perturber/perturbed galaxy mass ratio of 1000, shocks
will develop if perigalacticon is less than ~ 30 perturbed galaxy
scale radii. For dE scale radii of ~ 1 kpc, this requires
rather close (i.e. rare) passages, and is therefore probably not
very effective on the outskirts of clusters (where pressure
induced star formation might be). However, shocks per se may not
be necessary to influence the star-formation rate, which in some
models is determined by a delicate balance of cooling and supernova
heating. Tidal shaking may be enough to superimpose on this
feedback cycle an environment-dependent modulation in the star
formation efficiency, which may help explain the environmental
variations in the dE fraction, and the episodic
bursts of star formation seen in local dE's.
However, we must emphasize that mechanisms such as pressure induced
star formation and tidal shaking can only provide a viable way to form
the large dE populations of clusters if a suitable reservoir of galaxies
exists. The mass function of field dwarf irregulars and HI clouds must
therefore have roughly the same slope as the dE mass function. The
data are really too sparse to tell whether this is the case. The
comparison of the dE and Irr luminosity functions certainly does not
support such a transition, as the Irr LF appears to be flat
(Binggeli et
al. 1988).
The slope of the HI mass-function from blind surveys
is perhaps somewhat steeper
(Kerr and Henning
1987;
Weinberg et
al. 1991;
Schade and
Ferguson 1994).
An obvious consequence of induced star formation is
that dE galaxies may have formed many of their stars after
the collapse of galaxy clusters. As this occurs rather late
in hierarchical models, dE galaxies should contain significant
components of stars with ages less than ~ 5 Gyr.
7.6.4. Stochastic Star Formation
A final link between dwarf irregulars and dwarf ellipticals
is the possibility that star formation in gas-rich dwarf galaxies
is stochastic, with short bursts followed by long periods of
dormancy
(Gerola et
al. 1980;
Tyson and Scalo
1988).
Such a mechanism is
not viable as an explanation for most dE's because they
should have large reservoirs of HI. However, only a few dozen dE's
have actually been searched for HI, leaving open the possibility
that some could be dormant dwarf irregulars. Particularly
attractive candidates are bright non-nucleated dE's, which
show the same spatial distribution in clusters as the dwarf
irregulars (see Sect. 6.1).
Only a few have been observed in HI, and none detected.
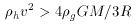
h is the density of the hot gas, and v,
M, R, and g
are the velocity, mass, radius, and mean gas density of the galaxy
(Takeda et
al. 1984).
Complete stripping of the central regions
requires that
v2 exceed the maximum binding force, which
for a King model is 
3.5 g 
2, where
is the galaxy velocity dispersion. To get a rough idea of the importance
of ram-pressure sweeping, consider a galaxy with = 25 km s-1
and a density nH = 1 cm-3 moving through an
external medium at 700 km s-1. According to the above formula,
complete sweeping would require a density in the external medium
n > 4 x 10-3 cm-3, something that is achieved
only within the central 100 kpc of the Virgo cluster core.
In addition to ram pressure,
evaporation, turbulent viscous stripping, and laminar stripping will
also act to remove the ISM from an infalling dwarf galaxy
(Cowie and
Songaila 1977;
Nulsen 1982).
Nulsen (1982)
estimates a typical mass loss rate of
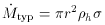
with
a gas density h, for all of these transport processes
(different ones acting in different regimes of galaxy velocity relative
to the sound-speed in the external medium). In more convenient units,
this becomes
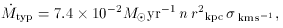
in a cluster with mean gas density
n = 10-4 cm-3 and velocity dispersion
= 700 km s-1.
Such densities are attained within 300 kpc of M87
(Fabricant and
Gorenstein 1983).
(Timescales are significantly shorter for the Coma cluster.)
in less than 10 Gyr would require
n > 10-4 cm-3, averaged over the orbit of
the galaxy. ROSAT observations probably exclude > 106 K gas
at the required densities for normal spiral galaxies
(Pietsch 1992).
nh Th (ignoring gravity).
A galaxy with a Tg = 100 K ISM of star-forming
density ng 1
cm-3 encountering a medium of
T 4 x 107 K
(the approximate temperature of the Virgo cluster gas found
by
Fabricant and
Gorenstein (1983),
will be pressure confined at densities
nh
10-6 cm-3. A galaxy falling into the cluster
for the first time at the present epoch encounters such densities
at a relatively low (subsonic) velocity, and may consequently have its ISM
compressed long before ram pressure and other gas removal mechanisms become
efficient. If the star-formation rate scales with some power
of the ISM density, such pressure confinement provides a natural
explanation for the existence of blue compact dwarf galaxies
(dwarf galaxies with enhanced central star formation) at the peripheries
of clusters
(Hoffmann et
al. 1989),
and also provides a mechanism for
converting Irr to higher-surface-brightness dE galaxies through a
period of enhanced star formation prior to gas stripping, similar
to the scenario proposed by
Davies and
Phillipps (1988).
nh-1 for a galaxy
moving through an isothermal cluster halo. The effect once again
will be to increase the star-formation rate during infall into
the cluster.