 -
V) requires the propagation of the
uncertainty in E (B - V) and the often-neglected but often-dominant
uncertainty in the adopted mean curve. This is given by
-
V) requires the propagation of the
uncertainty in E (B - V) and the often-neglected but often-dominant
uncertainty in the adopted mean curve. This is given by



3.1 Using a Global Mean Curve
If there is no specific information available about the wavelength dependence of the extinction along a sightline of interest then the only alternative is to adopt some globally defined mean curve and perform a realistic error analysis. This is the least attractive of the three cases discussed here, but is by far the most commonly used. The average Galactic extinction curves from either Seaton (1979; see Figure 1) or Savage & Mathis (1979) are often adopted for dereddening UV data. These should now be superseded by the use of an R-dependent curve computed for the case R = 3.1 (see Section 2.2). Figure 1 shows the R = 3.1 curve from CCM (dotted line) and a new determination of the R = 3.1 case (solid line) which is described in the Appendix to this paper. This new curve aims to reproduce the detailed wavelength dependence of the R = 3.1 extinction law and has been constructed to account for bandpass effects properly in optical/IR extinction data and to reproduce the observed broad-, intermediate-, and narrow- band extinction measurements. The curve is thus suitable for dereddening multiwavelength spectrophotometric observations and can be used to derive the average extinction relationships in any photometric system.
A complete evaluation of the likely error in a dereddened relative
energy distribution m ( -
V) requires the propagation of the
uncertainty in E (B - V) and the often-neglected but often-dominant
uncertainty in the adopted mean curve. This is given by
-
V) requires the propagation of the
uncertainty in E (B - V) and the often-neglected but often-dominant
uncertainty in the adopted mean curve. This is given by
where k (
The large database of ANS satellite extinction measurements from
Savage et al. (1985)
shows that the 1-
a
k ( b
These values (multiplied by the derived
E (B - V)) give the uncertainty in the final relative energy
distribution m (
Sometimes E (B - V) is not known a priori and is estimated by
``ironing out'' the 2175 Å extinction bump using an assumed
extinction curve shape (e.g., see
Massa et al. 1983).
In many cases, uncertainties in E (B - V) as small as 0.01-0.02 mag for
moderately reddened objects have been quoted from this process. This
is incorrect! The normalized ``height'' of the 2175 Å extinction
bump - which is the quantity that is important in the ironing-out
process - has a 1-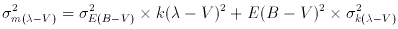
 - V)
represents the normalized extinction curve
E (
- V)
represents the normalized extinction curve
E ( - V) / E (B -
V). If absolute fluxes are desired, then the
uncertainty in the assumed value of R must also be incorporated (two
additional terms on the righthand side of eq. 1, similar to the current
terms but with R substituted for k (
- V) / E (B -
V). If absolute fluxes are desired, then the
uncertainty in the assumed value of R must also be incorporated (two
additional terms on the righthand side of eq. 1, similar to the current
terms but with R substituted for k ( - V)).
- V)).
 scatter at 1500 Å is
scatter at 1500 Å is
 k(15-V) = 0.74, based on ~ 400
sightlines with E (B - V)
k(15-V) = 0.74, based on ~ 400
sightlines with E (B - V)
 0.5. (Only relatively large values
of E (B - V) were considered in
order to minimize the effects of spectral mismatch error and random
noise on the
0.5. (Only relatively large values
of E (B - V) were considered in
order to minimize the effects of spectral mismatch error and random
noise on the  measurement.) To
extend this analysis to other
wavelengths, we computed the standard deviation at each wavelength
point for the 80 curves shown in
Figure 2, and then scaled the result
to match the ANS value at 1500 Å. (The actual standard
deviation at 1500 Å for the 80 IUE curves is somewhat higher
than the ANS result because of the bias in
Figure 2 toward
extreme extinction curves). The resultant values of
measurement.) To
extend this analysis to other
wavelengths, we computed the standard deviation at each wavelength
point for the 80 curves shown in
Figure 2, and then scaled the result
to match the ANS value at 1500 Å. (The actual standard
deviation at 1500 Å for the 80 IUE curves is somewhat higher
than the ANS result because of the bias in
Figure 2 toward
extreme extinction curves). The resultant values of
 k(
k( -V) are shown by the
thick dotted curve near the
bottom of Figure 2 (labeled ``
-V) are shown by the
thick dotted curve near the
bottom of Figure 2 (labeled `` '') and are listed at selected
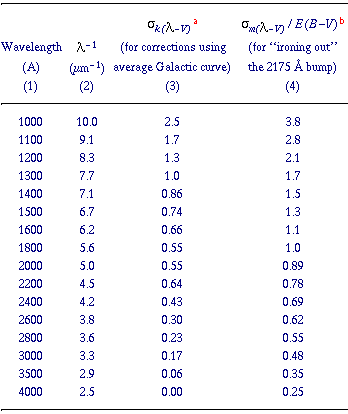
wavelengths in the third column of Table 1. This
estimate of
'') and are listed at selected
wavelengths in the third column of Table 1. This
estimate of
 k(
k( -V) should be adopted
whenever the average Galactic
extinction curve is used for dereddening an observed energy
distribution. The uncertainties approach zero for 1/
-V) should be adopted
whenever the average Galactic
extinction curve is used for dereddening an observed energy
distribution. The uncertainties approach zero for 1/ < 3 µm-1
due to the curve normalization. The quantity E (B - V) is
usually derived directly from photometry and often has an easily
quantifiable uncertainty; thus the computation of
< 3 µm-1
due to the curve normalization. The quantity E (B - V) is
usually derived directly from photometry and often has an easily
quantifiable uncertainty; thus the computation of
 2m(
2m( -V) from eq. 1
is straightforward.
-V) from eq. 1
is straightforward.
 -V)
-V)  E
(
E
( - V) / E (B - V). These
values of
- V) / E (B - V). These
values of  k (
k ( -V) should be inserted
into Eq. 1 to compute the uncertainty in a corrected relative energy
distribution m (
-V) should be inserted
into Eq. 1 to compute the uncertainty in a corrected relative energy
distribution m ( - V)
when there is no information available about the true
shape of the extinction law along the sightline and the average
Galactic curve is adopted by default.
See Section 3 in the text.
- V)
when there is no information available about the true
shape of the extinction law along the sightline and the average
Galactic curve is adopted by default.
See Section 3 in the text.
 - V)
when an object is dereddened by ``ironing out'' the 2175 Å bump
using the average Galactic extinction curve. See
Section 3.1 in the text.
- V)
when an object is dereddened by ``ironing out'' the 2175 Å bump
using the average Galactic extinction curve. See
Section 3.1 in the text.
 scatter of
about ± 20% around its mean
value (from the data in Figure 2 and
Savage et al. 1985).
Thus the
uncertainty in an E (B - V) measurement derived from the bump must be
considered to have a similar relative uncertainty. Since bump strength
does not correlate well with other aspects of UV extinction, such as
the slope of the linear component or the strength of the far-UV rise
(FM), the uncertainty in an energy distribution dereddened this way can
be estimated by using eq. 1 with
scatter of
about ± 20% around its mean
value (from the data in Figure 2 and
Savage et al. 1985).
Thus the
uncertainty in an E (B - V) measurement derived from the bump must be
considered to have a similar relative uncertainty. Since bump strength
does not correlate well with other aspects of UV extinction, such as
the slope of the linear component or the strength of the far-UV rise
(FM), the uncertainty in an energy distribution dereddened this way can
be estimated by using eq. 1 with  E(B-V)
E(B-V)  20% and the
values of
20% and the
values of  k(
k( -V) from
Table 1. The result of this
calculation needs to be modified somewhat by removing the signature of
the 2175 Å bump. The final estimate of
-V) from
Table 1. The result of this
calculation needs to be modified somewhat by removing the signature of
the 2175 Å bump. The final estimate of  2m(
2m( -V)
computed this way is listed in the last column of
Table 1. Multiplying
these values by E (B - V) gives the uncertainty in a dereddened relative
energy distribution. The values in Table 1 agree
well with estimates
-V)
computed this way is listed in the last column of
Table 1. Multiplying
these values by E (B - V) gives the uncertainty in a dereddened relative
energy distribution. The values in Table 1 agree
well with estimates
 2m(
2m( -V) at 1500,
1800, 2200, 2500, and 3300 Å
derived from the ANS data of
Savage et al (1985),
and are consistent with the analysis of
Massa (1987).
-V) at 1500,
1800, 2200, 2500, and 3300 Å
derived from the ANS data of
Savage et al (1985),
and are consistent with the analysis of
Massa (1987).