The UV Region

CCM noted a correlation between the value of R^-1 (as determined from IR/optical photometry) and the values of A() / A(V) (i.e., total extinction at normalized by total extinction at V) at UV wavelengths using parametrized extinction curves for a subset of 29 stars from the FM sample. They consequently derived a complex polynomial expression to reproduce the wavelength- and R- dependences. We approach the problem slightly differently and note that the essence of the CCM result is two correlations involving the coefficients of the FM fitting function originally used to parametrize the extinction curves studied by CCM. We thus derive the functional forms of these correlations and retain the FM fitting function to compute the values of E ( - V) / E (B - V) for wavelengths < 2700 Å

Figure 5 illustrates the two correlations. The top panel shows a plot of the FM parameter c2 (representing the slope of the linear UV extinction component) vs. R^-1 (filled circles) along with a least squares estimate of the linear relationship between the two (dashed line). The data are for a subset of the FM sample for which IR photometry could be used to deduce the value of R (see below), with the addition of the sightline toward HD 210121 (Welty & Fowler 1992; Larson et al. 1996). This represents the only convincing correlation between R and the properties of the UV extinction curve (see, e.g., Jenniskens & Greenberg 1993). The equation of the least-squares fit to the data is

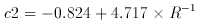(A1)

No physical interpretation or significance is placed on the form of the adopted functional relationship between R and c2; it is merely that which best reproduces the observed correlation. We note, however, that the intrinsic slope of extinction in the optical region is proportional to R^-1, and that eq. A1 thus simply implies that the slopes of the extinction curves in the UV and optical vary together in a linear manner - as optical extinction steepens, UV extinction steepens.

Figure 5. Left Panel: Slope of the UV linear extinction component c2 plotted against R-1 (filled circles) for 31 sightlines from the Fitzpatrick & Massa 1990 (FM) sample plus HD 210121 (at R-1 = 0.45). The adopted linear relationship between these quantities is indicated with the dashed line and given by c2 = -0.824 + 4.717R-1. Right Panel: Intercept of the UV linear extinction component c1 plotted against the linear slope c2 (filled circles) for the full set of ~ 80 extinction curves from the FM catalog. The adopted linear relationship between these parameters is indicated by the dashed line and given by c1 = 2.030 - 3.007 c2. The relationship between c1 and c2 implicit in the CCM formula is shown by the dotted line.

The bottom panel of Figure 5 shows the well-known relationship between slopes (c2) and intercepts (c1) of the linear background component (FM; Carnochan 1986; Jenniskens & Greenberg 1993). The data are for the full set of 80 curves from FM, plus HD 210121, and minus the Orion Nebula stars (HD 36982, 37022, 37023, and 37061) which suffer from scattered light contamination (which mainly affects the linear intercept). The equation of the least squares fit to this relationship (dashed line), is

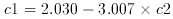(A2)

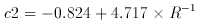
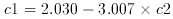
We use the following mean values for the other four parameters required to specify UV extinction curves with the FM formula: x0 (bump position) = 4.596 µm^-1; (bump width) = 0.99 µm^-1; c3 (bump strength) = 3.23; and c4 (FUV curvature) = 0.41.