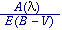The Optical/IR Region
A common way of representing the wavelength dependence of extinction in
the optical and IR regions is to draw a smooth curve through the values
of E (
- V) / E (B -
V) (or some other curve normalization) derived
from Johnson UBVRIJHKLM photometry, assuming that these represent
the monochromatic values of the extinction at the filter effective
wavelengths eff
(e.g., CCM,
Martin & Whittet 1990).
This
procedure does not accurately yield the monochromatic extinction
curve because it ignores the wavelength dependence of extinction across
the width of an individual filter. Extinction decreases towards longer
wavelengths in the optical/IR region and therefore the value of
eff for a reddened
star is shifted to a longer wavelength
than for an identical unreddened star. An extinction measurement made
by comparing photometric indices for two such stars (i.e., the ``pair
method'') will always overestimate the monochromatic extinction in the
neighborhood of eff because stellar emergent fluxes in the
optical/IR decrease towards longer wavelengths (for early-type stars).
The magnitude of this effect depends on how much the true extinction
curve varies across the filter. A broadband E ( - V) / E (B - V)
measurement will also be influenced by the intrinsic energy
distributions of the stars used in the pair method and by the total
amount of extinction.
The approach taken here is to find the wavelength dependence of the optical/IR extinction curve which reproduces the photometric extinction measurements when synthetic photometry of an artificially reddened stellar energy distribution is compared with that of identical but unreddened star. To represent the stellar energy distribution, an ATLAS9 model atmosphere from R.L. Kurucz (with Teff = 30000 K and log g = 4.0) is used, along with an adopted value of E (B - V) = 0.5. Synthetic photometry is performed to yield measurements in the broadband Johnson UBVRIJHKLM system and the intermediate band Strömgren uvby system. 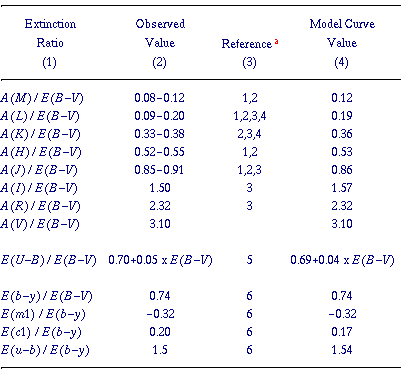The first step is to determine the curve shape for the mean R = 3.1 case and then to define the nature of the variation with R. The first two columns of Table 2 list the photometric extinction ratios (in both the Johnson and Strömgren systems) and their observed values, which the R = 3.1 extinction curve is required to reproduce. References to the observations are given in Column 3. In addition, the curve is constrained to reproduce the mean narrowband measurements in the 3400-7900 Å region published by Bastiaansen (1992), which are assumed to represent the monochromatic values of the extinction for the case R = 3.1 at the filter central wavelengths.
|
a References: 1 = Rieke & Lebofsky 1985; 2 = Whittet 1988; 3 = Schultz & Wiemer 1975; 4 = Savage & Mathis 1979; 5 = FitzGerald 1970; 6 = Crawford 1975 |
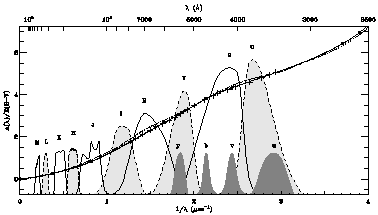
Figure 6 shows the shape of the monochromatic
extinction curve which
best satisfies these requirements (thick solid curve), plotted as total
extinction A()
normalized by E (B - V). The arbitrarily scaled
profiles of the Johnson and Strömgren filters are indicated, and
the Bastiaansen data shown by the small plus signs (``+''). The
agreement between the R = 3.1 curve and the Bastiaansen data is clear
from the figure. The fourth column of Table 4
gives the values of the
photometric extinction ratios produced by the curve, also in very good
agreement with the observations.
|
Figure 6. A new estimate of the wavelength
dependence of extinction in
the IR/optical region for the case R = 3.1 (thick solid curve). Plus
signs represent the extinction data from
Bastiaansen 1992,
normalized
to R = 3.1; the dotted line shows the CCM curve for R = 3.1. The
arbitrarily scaled profiles of the Johnson UBVRIJHKLM and
Strömgren uvby filters are shown for comparison. The new
curve was constrained to reproduce the broad- and intermediate-band
filter-based extinction measurements listed in
Table 2 and to fit the
Bastiaansen data. For |
For wavelengths longward of 2700 Å (1/ < 3.7 µm-1),
the R = 3.1 curve is defined by a cubic spline interpolation between a
set of optical/IR anchor points (filled circles) and a pair of UV
anchor points (filled squares). The values of the UV anchors (at 2700
Å and 2600 Å) are determined by the FM fitting function for the
case R = 3.1 (see above) and assure a smooth junction between the
optical and UV regions at 2700 Å. The anchor at 0
µm-1 is
fixed at 0 (i.e., no extinction at infinite wavelength) and the values
of the other six optical/IR points were adjusted iteratively to find
the curve shape which best reproduced the extinction observations. The
wavelengths chosen for the spline anchor points are somewhat arbitrary,
although points in the IR, the optical normalization region, and the
near-UV are clearly required. The wavelengths and values of the spline
anchors for the R = 3.1 curve are given in
Table 3.
| Wavelength | -1
| 
|
| (A) | (µm-1) | |
| (1) | (2) | (3) |
 | 0.000 | 0.000 |
| 26500 | 0.377 | 0.265 |
| 12200 | 0.820 | 0.829 |
| 6000 | 1.667 | 2.688 |
| 5470 | 1.828 | 3.055 |
| 4670 | 2.141 | 3.806 |
| 4110 | 2.433 | 4.315 |
| 2700 | 3.704 | 6.265 |
| 2600 | 3.846 | 6.591 |
Note the slope of the derived extinction curve does not approach
zero as 1/ approaches
zero. We sacrificed this physically
expected requirement in order to achieve a better fit to the Johnson IR
photometry and to preserve the simplicity of the fitting procedure. A
zero slope could have been guaranteed by, for example, adopting a power
law to represent the extinction; but no single power law can reproduce
the IR photometry to an acceptable level. The new curve should be
treated as very approximate at wavelengths beyond the limit of the
M band (i.e., at > 6
µm).
The overall R-dependence of the optical/IR curve is relatively easy
to incorporate by the following adjustments in the spline anchors: (1)
the UV points are computed by the FM fitting function using the
coefficient values given above, including the R-dependent value of
c2; (2) the IR points at 1/
< 1 µm-1 are simply
scaled by R/3.1, since the shape of the far-IR extinction is believed
to be invariant (see Section 2.1 and below);
and (3) the optical points are
vertically offset by an amount R-3.1, with slight corrections made to
preserve the normalization. Without these corrections (which are less
than 0.015 over the range R = 2 to 6) the extinction curves would
drift away from the standard normalization, i.e., E (B - V) = 1, by a
few hundredths of a magnitude as R departed from the value 3.1.
Table 4 gives formulae for computing the
R-dependent values of the
optical spline anchors. The corrections just noted are manifested
in the departure of the linear term from a value of 1.0 and in the
higher order term for the 4110 Å point.
| Wavelength | -1
|
|
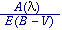
| (A) | (µm-1) | |
| (1) | (2) | (3) |
| 6000 | 1.667 | -0.426 + 1.0044 x R |
| 5470 | 1.828 | -0.050 + 1.0016 x R |
| 4670 | 2.141 | 0.701 + 1.0016 x R |
| 4110 | 2.433 | 1.208 + 1.0032 x R - 0.00033 x R2 |
It is not obvious a priori that the above adjustments in the spline should produce the proper curve shapes in the relatively large gaps between the 4 points in the optical normalization region and the UV or IR regions. However, it will be shown below that the resultant curves are in good agreement with observations.