


2.7. Conclusions on H0
The progress in determining the extragalactic distance scale has been dramatic. The ladders yield values convergent within 10%, which is compared to a factor 1.6 disagreement in the early nineties. A new uncertainty, however, becomes manifest in the Galactic distance scale: there is a 15-20% uncertainty in the distance to LMC. Therefore, we may summarise
as a currently acceptable value of the Hubble constant.
This agrees with that from HST-KP
(Mould et al. 1999)
up to the
uncertainty from the LMC distance, though we followed a different path
of argument. This allows
H0 = 90 at the high end (if Tonry et al's SBF is weighted)
and 60 at the low end (if the SNeIa results are weighted).
Note that H0 from both EPM and gravitational lensing are
consistent with the ladder value for (m - M)LMC = 18.5. With
the shorter LMC distance the overlap is marginal.
The short LMC distance will also cause trouble for the
H0-age
consistency. The LMC distance modulus of m - M = 18.25 would
raise the
lower limit of H0 to 72, and increase the lower limit of age
from
In the future it is likely that more effort will be expended for geometric
methods. The great advantage is that it is free from errors
arising from the chemical composition. In the surface brightness method,
the chemical composition may still enter
into the game, but its effect is tolerable and can even be reduced
to a negligible level by using near infrared observations.
Ultimately, gravitational wave observations could provide us with a novel
method. For instance, for coalescing binary neutron stars the distance can be
calculated as d ~
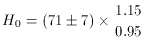
 11.5 Gyr to
11.5 Gyr to
 14.5 Gyr at the same time.
There is then no solution for a
14.5 Gyr at the same time.
There is then no solution for a
 = 0
universe. With a non-zero
= 0
universe. With a non-zero  , a
unique solution is H0
, a
unique solution is H0
 72,
72,

 0.25,
0.25,

 0.75
with coeval globular cluster formation (see Figure 6 below).
0.75
with coeval globular cluster formation (see Figure 6 below).
 -2
-2
 -1
-1
 -1,
where
-1,
where  is
metric perturbations,
is
metric perturbations,  is the
frequency and
is the
frequency and  =
=
 /
/
 is a characteristic time of the collapse
(Schutz 1986).
The position of the object may be difficult to infer,
but there might be a gamma ray burst associated with the
coalescence.
is a characteristic time of the collapse
(Schutz 1986).
The position of the object may be difficult to infer,
but there might be a gamma ray burst associated with the
coalescence.