3.3. Running Couplings

Grand Unified Theories point to such an explanation - a unified model from which one can derive the values and ratios of the coupling constants. In these unification schemes, the three Standard Model coupling constants derive from one unified coupling (which is still arbitrary at this level). The logarithmic running of coupling strength with energy, derived from renormalization theory, leads to the large ratio between unification scale and the proton mass. Although gravity is not included in these theories, the inferred unification scale (10¹⁶ GeV) is close to the Planck mass; the running couplings thus account for most of the ``largeness'' of the astrophysical Large Numbers.

Phenomenological coupling constants such as those we have been using (e.g., ) are not really constant but ``run'' or change with energy scale (Wilczek 1999). The vacuum is full of virtual particles which are polarized by the presence of a charge. An electrical charge (or a weak isospin charge) attracts like charges, which tend to screen its charge as measured from far away. At small distances there is less screening, so the charge appears bigger, so the effective coupling grows with energy. On the other hand a strong color charge attracts mostly virtual like-color charged gluons, so it is antiscreened and the coupling changes with the opposite sign - it gets weaker at high energy, and is said to display ``asymptotic freedom''. The freedom comes about from the antiscreening by gluons. ⁽⁷⁾

The bookkeeping of how the constants change with the energy scale M of interactions is done by renormalization group calculations. These show that the running coupling constant of U(1), ₁ = g₁², obeys

(9)

where the sum is over the charges Q_i of all fermions of mass less than M. The amount of charge screening by virtual particles increases if the vacuum contains more degrees of freedom that can be excited at a given energy. If all fermions in the Standard Model are included (and no more), the total sum on the right side is 14/3, yielding a slope of -14/9.

For SU(3), there is again a screening term depending on the number of color-charged fermions, but there is also an antiscreening term from the (known number of) gluons,

(10)

where n_f is the number of quark flavors of mass less than M. The factor of 11 from gluons dominates if the number of quark flavors is not too large, giving asymptotic freedom. In the Standard Model, n_f = 6, yielding a slope of + 7/4.

The running of couplings depends on the particle degrees of freedom at each energy scale, that is, counting virtual particles with rest mass below that energy. Thus in reality the slopes change with energy scale and with the addition of new species, if there are any.

It has been known for over 20 years that the gauge groups of the Standard Model fit nicely into larger groups of certain Grand Unified Theories (GUTs), the simplest ones being SU(5) and SO(10). The coupling constants of SU(3), SU(2), U(1) all approach each other logarithmically, merging at the GUT scale, about 10¹⁶ GeV. In recent years measurements of the couplings near m_Z have steadily improved and for some GUTs (such as minimal SU(5)) the three couplings no longer meet at a point; however, the agreement survives impressively well in supersymmetric models (Langacker and Polonsky 1994), or in models such as SO(10). There is thus some reason to believe that these models work up to the large scale of unification, which is already close to the Planck mass.

⁷ The reason for the difference is related to the zero point energies being opposite for fermion and boson modes, which also enters into considerations about their cancelling contributions to the cosmological constant in supersymmetric vacua. Back.
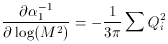
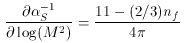