


3.4. Derivation of mPlanck/mproton
By the same token, if one of these GUTs is correct, it will provide
a derivation of the
 1,
1,
 2,
2,
 3 coupling constants at any
scale from one
unified constant
3 coupling constants at any
scale from one
unified constant  U
at the unification scale.
Recall that the mass of the proton is fixed by the scale at
which the SU(3) coupling diverges. Because of the slow
variation of coupling with energy,
this takes a large range of energy and leads to a
large ratio of proton to unification mass.
U
at the unification scale.
Recall that the mass of the proton is fixed by the scale at
which the SU(3) coupling diverges. Because of the slow
variation of coupling with energy,
this takes a large range of energy and leads to a
large ratio of proton to unification mass.
We can run through a toy calculation as follows. Assuming the degrees of
freedom are constant, the inverse couplings just depend
linearly on the log of the energy scale, so (9)
and (10) can be trivially integrated. Equating them at
the unification scale MU,
 1(MU) =
1(MU) =
 3(MU),
yields
3(MU),
yields
Naiively plugging in the standard model numbers (which give 2.1
for the denominator), and the values
The numerical factors here are just approximate,
but are exactly computable within the
framework of supersymmetric GUTs and yield a unification scale of
MU
Formulae very similar to (12) have appeared for many years
(see, for example, eq. (54) of
Carr and Rees 1979).
The rationale has always centered (as it does here) on the logarithmic
divergences of renormalization but in the context of supersymmetry the
derivation is much crisper - it comes in the framework of
rigorous derivations in a well-motivated theory now being tested
(Wilczek 1998).
If this guess about unification is correct,
we have most of the explanation of
the large numbers of astrophysics, subject to the value
of one independent, apparently
arbitrary coupling-constant parameter
(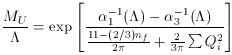
 1
1
 (60)-1 and
(60)-1 and
 3
3

 _S
_S
 0.12 for
the coupling constants at the Z scale, yields a mass ratio
of MU / MZ
0.12 for
the coupling constants at the Z scale, yields a mass ratio
of MU / MZ
 exp[(60-8)/2.1] = 1011.
This toy estimate is wrong in several details (most notably, not having
included supersymmetry) but correctly
illustrates the main point, that there exists an exact calculation
that yields a large ratio of fundamental masses, roughly
exp[(60-8)/2.1] = 1011.
This toy estimate is wrong in several details (most notably, not having
included supersymmetry) but correctly
illustrates the main point, that there exists an exact calculation
that yields a large ratio of fundamental masses, roughly
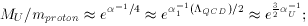
 1016
GeV. In this framework, this is essentially the explanation of the
``weakness'' of gravity, the smallness of
mproton/mPlanck. Since
mPlanck
1016
GeV. In this framework, this is essentially the explanation of the
``weakness'' of gravity, the smallness of
mproton/mPlanck. Since
mPlanck
 103
MU there are three of
the nineteen orders of magnitude still to be accounted for,
presumably by the final unification with gravity.
103
MU there are three of
the nineteen orders of magnitude still to be accounted for,
presumably by the final unification with gravity.
 U or
gU),
a moderately small number (of the order of 1/25).
The value of mproton /
MU depends exponentially on
U or
gU),
a moderately small number (of the order of 1/25).
The value of mproton /
MU depends exponentially on
 U (and hence also on
U (and hence also on
 ).
Changes of a few percent in the couplings lead to order-of-magnitude variations
in the astrophysical Large Numbers, enough to cause
qualitative change in the behavior of
the astrophysical world. The fine structure
constant thereby becomes a candidate
for selective tuning connected to obtaining
a suitable strength for gravitation!
).
Changes of a few percent in the couplings lead to order-of-magnitude variations
in the astrophysical Large Numbers, enough to cause
qualitative change in the behavior of
the astrophysical world. The fine structure
constant thereby becomes a candidate
for selective tuning connected to obtaining
a suitable strength for gravitation!