


4.2. Quark Masses and the Stability of the Proton and Deuteron
It has long been noted that the stability of the proton depends on
the up and down quark masses, requiring
md - mu
 Eem
Eem

 3/2
mproton to overcome the
extra electromagnetic mass-energy Eem of
a proton relative to a neutron.
Detailed considerations suggest that md -
mu is quite finely tuned, in the
sense that if it were changed by more than a fraction of its value
either way, nuclear astrophysics as we know it would radically change.
3/2
mproton to overcome the
extra electromagnetic mass-energy Eem of
a proton relative to a neutron.
Detailed considerations suggest that md -
mu is quite finely tuned, in the
sense that if it were changed by more than a fraction of its value
either way, nuclear astrophysics as we know it would radically change.
Quarks being always confined never appear ``on-shell'' so their masses
are tricky to measure precisely. A recent review by
Fusaoka and Koide (1998)
gives mu = 4.88 ± 0.57 MeV, md =
9.81 ± 0.65 MeV,
larger than the 0.511 MeV of the electron but negligible
compared to the 938.272 MeV mass of the proton,
939.566 MeV of the neutron, or 1875.613 MeV of the deuteron.
On the other hand small changes in
md-mu can have surprisingly profound
effects on the world through their effect on the relative
masses of the proton, neutron and deuteron.
If mn < mp the proton is unstable and
there are no atoms, no chemistry.
It is thus important that mn > mp, but
not by too much since the neutron becomes too unstable.
The neutron  - decay
rate is as small as it is only because
of the small n, p mass difference: it is
closely controlled by the phase space suppression.
With a small increase in the mass difference the neutron
decays much faster and the deuteron becomes unstable,
also leading to radical changes in the world.
- decay
rate is as small as it is only because
of the small n, p mass difference: it is
closely controlled by the phase space suppression.
With a small increase in the mass difference the neutron
decays much faster and the deuteron becomes unstable,
also leading to radical changes in the world.
Consider for example the pp reaction,
which begins the conversion of hydrogen to helium in the Sun.
The endpoint of this reaction is only 420 keV, meaning that if
the deuteron were 420 keV heavier (relative to the other
reactants) the reaction would not even be
exothermic and would tend to run in the other direction.
Although the quark masses are uncertain, we can estimate
the effect a change in their difference would have.
To the extent that the neutron and proton structures
preserve isospin symmetry, the calculation is simple
since their masses just change additively in response to a change in
the quark masses. For the deuteron the story is a little more involved
because of the effect on the nuclear potential.
Consider a transformation to a different world with different values
of the quark and electron masses,
We then have
We have defined a key parameter,
the amount of change in the mass difference,
Now consider the effect of this transformation on the reactions
The heat balance of these reactions in our world is
In the transformed world,
a hydrogen atom (HI) is unstable (through the proton capturing
the electron and converting into a stable neutron) if
In atoms, or in plasmas where electrons are readily available,
the neutron becomes the energetically favored state. As
For positive
on the pp reactions
p + p -> D + e+ +
The pp -> D direction stops being energetically favored if
In the Big Bang plasma, the abundance of deuterons in this world is
highly suppressed, so there is no stepping-stone to
the production of helium and heavier
nuclei, so the universe initially is made of essentially
pure protons. (9)
Furthermore, since the pp chain is broken,
cosmic chemical history would be radically altered: For example,
there is no two-body reaction for nucleosynthesis
in stars to get started so main-sequence stars
would all have to use catalytic cycles such as the CNO process
(where the heavy catalysts would have to be generated in
an early generation under degenerate conditions).
As long as stable states of heavier nuclei exist,
some of them would likely be produced occasionally in degenerate
deflagrations (akin to Type Ia supernovae).
As
Above some threshold, stable states of heavier nuclei
disappear altogether and there is no nuclear physics at all.
Thresholds for these effects are shown in figure 1.
Note that md-mu is bounded within a
small interval - if it departs from this range one way or another
a major change in nuclear astrophysics results.
The total width of the interval, of the order of an MeV,
depending on how drastic the changes are, should be compared
with the values mu
We should consider these constraints with the kind of additional
joint constraints that unification symmetry is likely to impose
on the fermion masses. For example, suppose that some symmetry
fixes the ratio md / me (e.g.,
Fukugita et al. 1999),
thereby fixing
9 The reactions are of course also
affected by couplings which enter into reaction rates. The
balance between the expansion rate and weak interaction rates
controls nucleosynthesis both in supernovae and in the Big Bang.
For example,
Carr and Rees (1979)
argue that avoiding a universe of nearly pure helium requires the weak
freeze-out to occur at or below the temperature equal to the
n, p mass difference, requiring
(mn - mp)3 >
mPlanck-1
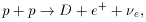
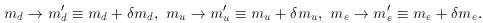
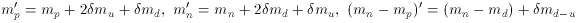
 md-u
md-u

 md -
md -
 mu.
mu.
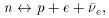
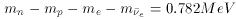
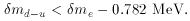
 md-u drops,
Big Bang nucleosynthesis first increases the
helium abundance to near 1, then makes most of the baryons
into neutrons. There would
be no hydrogen atoms except a small residue of deuterium.
Synthesis of heavy elements could still continue (although
as shown below, with the nuclei somewhat altered). Indeed
there is no Coulomb barrier to keep the neutrons apart and hardly any
electrons to provide opacity, so the
familiar equilibrium state of main-sequence stars would disappear.
The effects get even more radical as
md-u drops,
Big Bang nucleosynthesis first increases the
helium abundance to near 1, then makes most of the baryons
into neutrons. There would
be no hydrogen atoms except a small residue of deuterium.
Synthesis of heavy elements could still continue (although
as shown below, with the nuclei somewhat altered). Indeed
there is no Coulomb barrier to keep the neutrons apart and hardly any
electrons to provide opacity, so the
familiar equilibrium state of main-sequence stars would disappear.
The effects get even more radical as
 md-u decreases
even more; rapid, spontaneous decay of a free proton to a neutron
happens if
md-u decreases
even more; rapid, spontaneous decay of a free proton to a neutron
happens if
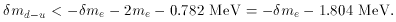
 md-u, we have the opposite
problem; neutrons and deuterons are destabilized.
First, we restrict ourselves to constant
md-u, we have the opposite
problem; neutrons and deuterons are destabilized.
First, we restrict ourselves to constant
 md+u
md+u

 md +
md +  mu = 0,
so changes in nuclear potential can be neglected.
Then we consider just the effect of the change in deuteron mass,
mu = 0,
so changes in nuclear potential can be neglected.
Then we consider just the effect of the change in deuteron mass,
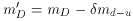
 e.
In our world the heat balance is
e.
In our world the heat balance is
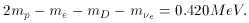
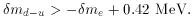
 md-u
increases, the valley of
md-u
increases, the valley of
 -stability
moves to favor fewer neutrons;
a free deuteron spontaneously fissions into two protons if
-stability
moves to favor fewer neutrons;
a free deuteron spontaneously fissions into two protons if
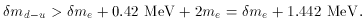
 5 MeV and md
5 MeV and md
 10 MeV,
or the mass of the proton, 1 GeV.
10 MeV,
or the mass of the proton, 1 GeV.
 md /
md /
 me, and we require
that mu > 0.
The resulting constraint is illustrated in figure 1.
me, and we require
that mu > 0.
The resulting constraint is illustrated in figure 1.
 -2
mproton-2
mW4. Back.
-2
mproton-2
mW4. Back.