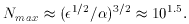4. TUNING LIGHT FERMION MASSES

4.1. Nucleons and Nuclei

Like the electronic structure of atoms, the basic structure of neutrons and protons depend hardly at all on any of the parameters. Ignoring for now the small effect of electric charge and quark mass, proton and neutron structure are the same, with labels related by isospin symmetry. Their internal structure and mass are entirely determined by strong QCD SU(3) gauge fields (gluons) interacting with each other and with the quarks. There are no adjustable parameters in the structure, not even a coupling constant, except for the setting of the energy scale. ⁽⁸⁾ Although these nucleon field configurations are not really ``solved'', the equations which govern them are known exactly and their structure can be approximately solved in lattice models of QCD which correctly estimate for example the mass ratios of the proton and other hadrons. Basically, the mass of the proton m_proton = 0.938 GeV is some calculable dimensionless number (about 5) times the energy scale _QCD fixed by the strong interaction coupling constant. The structure and mass of hadrons is as mathematically rigid as a Platonic solid. Even so, because n and p are so similar, the stability of the proton is very sensitive to the electromagnetic effects and to the much smaller, and seemingly unrelated, up and down quark masses, which break the symmetry.

Strong interactions not only create isolated hadronic structures, but also bind them together into nuclei. Although the individual hadrons are to first approximation pure SU(3) solitons, nuclear structure is also directly influenced by quark masses, especially through their effect on the range of the nuclear potential. The strong interactions of hadrons can be thought of as being mediated by pions, which have relatively low mass (m(₀) = 135 MeV) and therefore a range which reaches significantly farther than the hadronic radius. The light quark masses determine the pion mass via breaking of chiral symmetry, m sqrt[m_proton(m_u + m_d)], and therefore the details of nuclear energy levels are sensitive to u and d masses.

The dependence of nuclear structures on quark masses and electromagnetic forces is hard to compute exactly but we can sketch the rough scalings. The nuclear binding energy in a nucleus with N nucleons is about E_nuc N m_proton where the specific binding energy per mass is about (m / m_proton)² (m_u + m_d) / m_proton 10^-2 and hence the typical separation is ^-1/2 m_proton^-1. The nuclear size therefore is typically R N^{1/3 -1/2} m_proton^-1. Larger nuclei develop increasing electromagnetic repulsion, scaling like E_em N²/R. They become unstable above a maximum charge where the nuclear and electrostatic energies match,

(13)

The basic reason for the number of stable nuclei is that the electromagnetic coupling is weak, but not extremely weak, compared to the strong interactions.

⁸ Ironically, the nucleon rest mass (which of course includes most of the rest mass of ordinary matter) is 99% dominated by the kinetic energy of the constituents, including roughly equal contributions from very light quarks and massless gluons. Back.