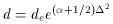10.2.2 Correction For Biases
In principle, once the above corrections have been applied,
the Dn- method can be used to estimate relative
distances. However there are two selection biases,
which potentially afflict any sample of galaxies chosen
in a diameter or magnitude limited way, that require correction. The first,
a ``Malmquist-like'' bias, affects principally those galaxies which are
not in rich clusters. As there are more galaxies at greater distances
in any sample limited by diameter or apparent brightness, there will be
more large/bright galaxies erroneously included in the sample from
larger distances than there are galaxies omitted from the sample at
smaller distances. Thus, a diameter limited sample is contaminated
by galaxies that are measured to be large for their dispersion.
This generates the illusion that galaxies are nearer than their true
distance and would generate spurious positive peculiar
velocities. Unless corrected, the effect of this would be to introduce a
scale change as if to overestimate the Hubble constant.
LFBDDTW show that the correction for this
depends on the size of the dispersion in the distance
estimator (i.e., ln Dn),
method can be used to estimate relative
distances. However there are two selection biases,
which potentially afflict any sample of galaxies chosen
in a diameter or magnitude limited way, that require correction. The first,
a ``Malmquist-like'' bias, affects principally those galaxies which are
not in rich clusters. As there are more galaxies at greater distances
in any sample limited by diameter or apparent brightness, there will be
more large/bright galaxies erroneously included in the sample from
larger distances than there are galaxies omitted from the sample at
smaller distances. Thus, a diameter limited sample is contaminated
by galaxies that are measured to be large for their dispersion.
This generates the illusion that galaxies are nearer than their true
distance and would generate spurious positive peculiar
velocities. Unless corrected, the effect of this would be to introduce a
scale change as if to overestimate the Hubble constant.
LFBDDTW show that the correction for this
depends on the size of the dispersion in the distance
estimator (i.e., ln Dn),  ,
and on the distribution of galaxies. If the latter is parameterized
as a power law in number density such that the number of field
galaxies in an annulus between r to r + dr is
n(r)dr / r, so that:
,
and on the distribution of galaxies. If the latter is parameterized
as a power law in number density such that the number of field
galaxies in an annulus between r to r + dr is
n(r)dr / r, so that:
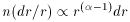 (23)
(23)
(for a uniform distribution of galaxies  = 3), then
the correction for the bias is given by equation 2.11 of LFBDDTW:
= 3), then
the correction for the bias is given by equation 2.11 of LFBDDTW:
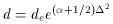 (24)
(24)
where de is the raw estimate of the distance and
d is the corrected value.
The correction is smaller for aggregates of galaxies, falling
as 1/N when there are N galaxies with independently estimated
distances de.
The second correction is applied only to galaxies in clusters
where the selection by diameter causes the cluster to have
an over-representation of large galaxies and an under-representation
of small ones. LFBDDTW estimated the size of the correction for
this effect by combining the galaxies with  > 100 km s-1
from clusters containing three or more galaxies using the preliminary
distance estimates and then by truncating the sample
at a range of diameters. The correction factors are tabulated in
their appendix B and can amount to a 10% correction for aggregates
at 6000 km s-1.
> 100 km s-1
from clusters containing three or more galaxies using the preliminary
distance estimates and then by truncating the sample
at a range of diameters. The correction factors are tabulated in
their appendix B and can amount to a 10% correction for aggregates
at 6000 km s-1.
The steps outlined above allow relative distances of aggregates
of galaxies to be determined self-consistently
and accurately from Dn- data for individual and cluster
elliptical galaxies. This is one of the 2 methods
of
Aaronson et
al. (1982):
distances are calculated
from the distance estimator and the parameters
of the flow model are derived
by maximizing the likelihood in the velocity field residuals.
The second method of Aaronson et al. (1982) (discussed in the context of
the Dn-
data for individual and cluster
elliptical galaxies. This is one of the 2 methods
of
Aaronson et
al. (1982):
distances are calculated
from the distance estimator and the parameters
of the flow model are derived
by maximizing the likelihood in the velocity field residuals.
The second method of Aaronson et al. (1982) (discussed in the context of
the Dn- method by LFBDDTW and by
Faber and Burstein
1989),
involves determining the distance to galaxies on the basis of
the observed velocity and a model of the velocity field and
using this to predict the velocity dispersion for a given diameter. The model
parameters are determined by maximizing the likelihood in the
Dn-
method by LFBDDTW and by
Faber and Burstein
1989),
involves determining the distance to galaxies on the basis of
the observed velocity and a model of the velocity field and
using this to predict the velocity dispersion for a given diameter. The model
parameters are determined by maximizing the likelihood in the
Dn- relation. The two methods each have advantages
depending on the exact application being
pursued;
Faber and Burstein
(1989)
give an extensive discussion of the pros and cons of each method and
develop a hybrid approach.
relation. The two methods each have advantages
depending on the exact application being
pursued;
Faber and Burstein
(1989)
give an extensive discussion of the pros and cons of each method and
develop a hybrid approach.



 method can be used to estimate relative
distances. However there are two selection biases,
which potentially afflict any sample of galaxies chosen
in a diameter or magnitude limited way, that require correction. The first,
a ``Malmquist-like'' bias, affects principally those galaxies which are
not in rich clusters. As there are more galaxies at greater distances
in any sample limited by diameter or apparent brightness, there will be
more large/bright galaxies erroneously included in the sample from
larger distances than there are galaxies omitted from the sample at
smaller distances. Thus, a diameter limited sample is contaminated
by galaxies that are measured to be large for their dispersion.
This generates the illusion that galaxies are nearer than their true
distance and would generate spurious positive peculiar
velocities. Unless corrected, the effect of this would be to introduce a
scale change as if to overestimate the Hubble constant.
LFBDDTW show that the correction for this
depends on the size of the dispersion in the distance
estimator (i.e., ln Dn),
method can be used to estimate relative
distances. However there are two selection biases,
which potentially afflict any sample of galaxies chosen
in a diameter or magnitude limited way, that require correction. The first,
a ``Malmquist-like'' bias, affects principally those galaxies which are
not in rich clusters. As there are more galaxies at greater distances
in any sample limited by diameter or apparent brightness, there will be
more large/bright galaxies erroneously included in the sample from
larger distances than there are galaxies omitted from the sample at
smaller distances. Thus, a diameter limited sample is contaminated
by galaxies that are measured to be large for their dispersion.
This generates the illusion that galaxies are nearer than their true
distance and would generate spurious positive peculiar
velocities. Unless corrected, the effect of this would be to introduce a
scale change as if to overestimate the Hubble constant.
LFBDDTW show that the correction for this
depends on the size of the dispersion in the distance
estimator (i.e., ln Dn),  ,
and on the distribution of galaxies. If the latter is parameterized
as a power law in number density such that the number of field
galaxies in an annulus between r to r + dr is
n(r)dr / r, so that:
,
and on the distribution of galaxies. If the latter is parameterized
as a power law in number density such that the number of field
galaxies in an annulus between r to r + dr is
n(r)dr / r, so that:



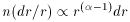
 = 3), then
the correction for the bias is given by equation 2.11 of LFBDDTW:
= 3), then
the correction for the bias is given by equation 2.11 of LFBDDTW: