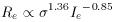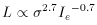10.3 Physical Basis
10.3.1 Power Law Relationships
There is no complete physical description of the structure and kinematics
of elliptical galaxies. However, starting from some simple
physical assumptions a rudimentary justification of the method can be
provided.
Sargent et al. (1977)
pointed out that the assumptions
that all elliptical galaxies have the same surface
brightness, L  R2
(Fish 1964)
and mass-to-light ratio (M/L), together
with the virial theorem relation M
R2
(Fish 1964)
and mass-to-light ratio (M/L), together
with the virial theorem relation M  R
R 2, lead to
the Faber-Jackson relation L
2, lead to
the Faber-Jackson relation L 
 4. These ideas
were extended by
Djorgovski & Davis
(1987) and
Dressler et
al. (1987b)
who developed the concept of a fundamental plane in the
3-space of log Ie log Re log
4. These ideas
were extended by
Djorgovski & Davis
(1987) and
Dressler et
al. (1987b)
who developed the concept of a fundamental plane in the
3-space of log Ie log Re log  where Ie is the
galaxy surface brightness within the half-light radius,
Re (or diameter Ae).
Combining the results of these three studies,
the equation of the fundamental plane is:
where Ie is the
galaxy surface brightness within the half-light radius,
Re (or diameter Ae).
Combining the results of these three studies,
the equation of the fundamental plane is:
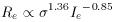 (25)
(25)
or expressed in terms of a modified Faber-Jackson relation:
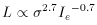 (26)
(26)
As Dressler et
al. (1987b)
show, there are only two
independent parameters in the three observables
Ae, Dn, and Ie, so that
Dn / Ae
is a function of
the normalizing surface brightness only. They find
Dn / Ae  Iex, where x = 0.8.
This, together with the empirical (Dn-
Iex, where x = 0.8.
This, together with the empirical (Dn- ) relation,
leads to a formulation of the modified Faber-Jackson relation which is almost
identical to equation (26). Thus the definition of Dn
combines the
parameters of the fundamental plane in such a way that it
is viewed edge-on and Dn is therefore a close to
optimal distance indicator. This is illustrated in
Figure 22
which shows the fundamental plane and its projections,
taken from
Faber et al. 1987.
They point out that the existence of the fundamental plane implies
there are no constraints on the global parameter relations
for elliptical galaxies other than the Virial Theorem.
This is perhaps the most important difference between the
Dn-
) relation,
leads to a formulation of the modified Faber-Jackson relation which is almost
identical to equation (26). Thus the definition of Dn
combines the
parameters of the fundamental plane in such a way that it
is viewed edge-on and Dn is therefore a close to
optimal distance indicator. This is illustrated in
Figure 22
which shows the fundamental plane and its projections,
taken from
Faber et al. 1987.
They point out that the existence of the fundamental plane implies
there are no constraints on the global parameter relations
for elliptical galaxies other than the Virial Theorem.
This is perhaps the most important difference between the
Dn- relation
and the Tully-Fisher methods; the latter, being a single parameter
relationship, requires the action of an extra physical constraint which is
presumably set during galaxy formation
(Gunn 1988).
Thus the Dn-
relation
and the Tully-Fisher methods; the latter, being a single parameter
relationship, requires the action of an extra physical constraint which is
presumably set during galaxy formation
(Gunn 1988).
Thus the Dn- relation depends on the physics of galaxy equilibrium rather than
the physics of galaxy formation.
relation depends on the physics of galaxy equilibrium rather than
the physics of galaxy formation.
| 
|

| 
|
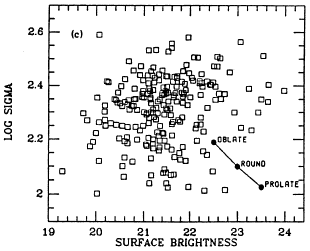
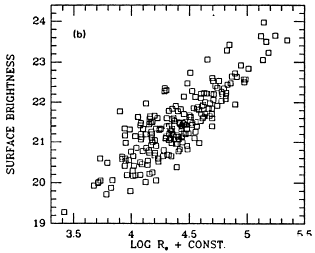
Figure 22. Structural parameters for group galaxies in the 7S
survey, taken from
Faber et
al. (1987).
(a) log  vs log Re; the
diagonal line of slope -0.5 is the constant mass locus. (b) Surface
brightness vs log Re, showing the fundamental plane
almost edge-on. (c) log vs log Re; the
diagonal line of slope -0.5 is the constant mass locus. (b) Surface
brightness vs log Re, showing the fundamental plane
almost edge-on. (c) log  vs
surface brightness, showing the fundamental plane nearly face-on; the
dots show the effect viewing an E3.6 oblate or prolate galaxy seen at
maximum elongation and as round in projection. (d) log vs
surface brightness, showing the fundamental plane nearly face-on; the
dots show the effect viewing an E3.6 oblate or prolate galaxy seen at
maximum elongation and as round in projection. (d) log  vs (log Re +
0.84 log Ie) showing the plane exactly edge-on. vs (log Re +
0.84 log Ie) showing the plane exactly edge-on.
|
The Dn- relation cannot be justified in terms of a detailed
physical model such as can be formulated for Type Ia supernovae or
Cepheids. A general physical description has been formulated
using power law relationships
between the structural and kinematic variables that illustrates
the sensitivity of the method to the assumptions.
relation cannot be justified in terms of a detailed
physical model such as can be formulated for Type Ia supernovae or
Cepheids. A general physical description has been formulated
using power law relationships
between the structural and kinematic variables that illustrates
the sensitivity of the method to the assumptions.



 R2
(Fish 1964)
and mass-to-light ratio (M/L), together
with the virial theorem relation M
R2
(Fish 1964)
and mass-to-light ratio (M/L), together
with the virial theorem relation M  R
R 2, lead to
the Faber-Jackson relation L
2, lead to
the Faber-Jackson relation L 
 4. These ideas
were extended by
Djorgovski & Davis
(1987) and
Dressler et
al. (1987b)
who developed the concept of a fundamental plane in the
3-space of log Ie log Re log
4. These ideas
were extended by
Djorgovski & Davis
(1987) and
Dressler et
al. (1987b)
who developed the concept of a fundamental plane in the
3-space of log Ie log Re log  where Ie is the
galaxy surface brightness within the half-light radius,
Re (or diameter Ae).
Combining the results of these three studies,
the equation of the fundamental plane is:
where Ie is the
galaxy surface brightness within the half-light radius,
Re (or diameter Ae).
Combining the results of these three studies,
the equation of the fundamental plane is: