7.2.3 Line-Width Definitions and Corrections
As mentioned in Sec. 7.2 the parameter used
in the TF relations for predicting
the luminosity for a particular galaxy is Vmax, the
maximum amplitude
of the rotation curve. If the dark matter distribution is isothermal
(implied by flat rotation curves), then
Vmax is a measure of mass, provided that the
distribution of mass within galaxies is similar (see
Sec. 7.3). Since galaxies have flat rotation
curves over much of their extent, Vmax should be
insensitive to
differing measurement techniques, and has the additional advantage of being
well defined. In the original formulation, Tully and
Fisher used the doppler width of the 21-cm line profile
measured at 20% of peak (W20), corrected for receiver
broadening and galaxy inclination (i.e., Wi =
W20/sin i ~ 2Vmax).
This was also the procedure used by Aaronson and collaborators. It has the
advantage of being conceptually simple and it is easy to compare between
different researchers when these minimally corrected line-widths are used.
The 21-cm line is particularly well suited to sampling the outer
rotation curves of galaxies
since the extent of detectable HI is often several times that of the visible
galaxy (e.g.
Roberts 1962;
Bosma 1981).
It is also relatively easy to detect
HI out to considerable distances (e.g. the Hercules Cluster at
V0 ~
11000 km s-1 with Arecibo). It is worth emphasizing that errors
in the corrected line-widths are likely to be the dominant source of
observational error, so a signal-to-noise level of 
10 is essential.
Other definitions
of rotational broadening have been used (e.g. W50),
particularly if the
signal-to-noise is low. While alternative definitions are acceptable,
in principle, the fact that estimates of Vmax using
W20 closely
correspond to those values obtained from classical rotation curves
via H
implies that
W20 is a
good choice. The use of different definitions for line-width become
important when trying to compare results from the H and
HI techniques, or even from different investigators.
Bottinelli et al. (1983, 1984) correctly pointed out that the simple inclination correction given above does not allow for the effects of the turbulent motion internal to the gas; these are expected to be a significant source of doppler broadening for low luminosity systems. Observations of significant line-widths for face-on systems (e.g. Lewis 1984) attests to the importance of this effect. Without a correction for turbulence, Wi, and hence Vmax, would be progressively over estimated with decreasing luminosity (mass), resulting in a curved TF relationship (e.g. Aaronson et al. 1986; Mould et al. 1989). Using the observed velocity ellipsoid for the flattest population I components in the Galaxy, Bottinelli et al. estimated the turbulence at ~ 15 km s-1. The amount of the correction was slightly inclination dependent due to the assumption of an anisotropic velocity ellipsoid. They then linearly subtracted this correction from the observed profile width and corrected for inclination to obtain 2Vmax.
Tully and Fouqué (1985) suggested a slight modification to the Bottinelli et al. procedure. They advocated an isotropic velocity dispersion for the HI and a quadrature subtraction of the turbulence term for dwarf galaxies on the grounds that the velocity profiles are more like Gaussians than the ``box car'' profiles of the higher luminosity galaxies. Their prescription for correcting line-widths is consequently more complicated as it also includes a smoothing function to ease the transition between the two correction regimes:
where W20 is the measured width at 20% of peak
intensity, Wt is the
expected 20% width due to turbulence (38 km s-1) for an isotropic
velocity dispersion of 10 km s-1, Wt is the
characteristic transition
width from ``horned'' to Gaussian shaped profiles (120 km s-1), and
finally, WRi = WR /
sini is the corrected rotational parameter
(~ 2Vmax). Note, that this procedure results in the
transition width (Wt) being a function of inclination.
These two correction schemes are essentially indistinguishable for
WRi
An optical alternative to HI velocity widths has been developed by
Rubin et al. (1985)
based on rotation curves measured at
H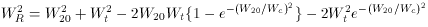
100 km s-1, but differ substantially from the case
of no turbulence correction. Obviously, care must be taken when
comparing corrected line-widths from different researchers. Naturally,
the calibrators and the sample galaxies should span a similar range in
luminosity and WR to the program galaxies in order to
minimize any systematic errors introduced by these correction procedures.
. This technique is
particularly promising because detection
efficiencies are high for telescopes in the 2-3 m class out to
velocities of ~ 10,000 km s-1; thus, they are competitive
with 21-cm line-widths obtained with the Arecibo telescope, while
offering full sky coverage. In addition, optical spectroscopy can be
applied in the crowded cores of more distant clusters, where the large
beam of even the Arecibo dish suffers from confusion. While the
H data can easily be corrected
for inclination, the correction
for internal turbulence in low luminosity systems is complicated by
outflow near star-forming regions.
Recently, Faber and Corteau (1989)
have re-examined the application of
H rotation curves for
estimating Vmax, and find good
agreement between optical and radio estimates.
Dressler and Faber
(1990b)
have used an optical version of the TF relation to
examine the velocity field in the vicinity of the ``Great Attractor''.