


7.2.2 Internal Extinction Corrections
The corrections for internal extinction are based on models, but these
have proven difficult to test due to a shortage of accurate
surface photometry. The approach usually taken assumes that spiral and
irregular galaxies are not optically thick, although the suggestion that
galaxies are opaque has been expressed by
Disney et
al. (1989) and
Valentijn (1990).
There are three general forms for the optically thin
models: (i) the light is assumed to be mixed evenly with the dust,
(ii) the dust is assumed to lie in an infinitely thin obscuring layer,
and (iii) a combination of the two, where the dust lies in a layer
of finite thickness with a portion of the light being unobscured.
While the second model is relatively simple and has some observational
basis, the
assumption of an infinitely thin absorbing layer results in a rapid
variation of extinction between i = 45°, and i =
90°. Available data suggest that this is too severe (i.e.,
Tully and
Fouqué 1985).
Tully and
Fouqué (1985)
discuss some of the problems with the first
two formulations given above and offer a compromise between these
extremes (the third model). This model is certainly the most
physically sound, and it appears to provide the best fit to the
available data. Under the assumptions of the third model the
extinction correction becomes:
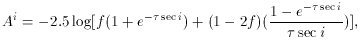 (12)
(12)
where as before, i is the
inclination and  is the optical
depth. The additional parameter
f is the fraction of the light that is unobscured by the dust
layer. Thus, f = 0.5 leads to the infinitely thin layer model, while
f = 0 leads to the model proposed by Holmberg.
Tully and
Fouqué (1985)
adopted
is the optical
depth. The additional parameter
f is the fraction of the light that is unobscured by the dust
layer. Thus, f = 0.5 leads to the infinitely thin layer model, while
f = 0 leads to the model proposed by Holmberg.
Tully and
Fouqué (1985)
adopted  ~ 0.55 for the
B band, f ~ 0.25, and
suggested that the data are better fit if the extinction for i >
80° is held at the value for 80°. At present, this simplistic
two-component model appears to be the most reasonable formulation for
the internal extinction within galaxies, provided that they are
optically thin. Surface photometry data over a broad wavelength range
would greatly help to clarify the values of f and
~ 0.55 for the
B band, f ~ 0.25, and
suggested that the data are better fit if the extinction for i >
80° is held at the value for 80°. At present, this simplistic
two-component model appears to be the most reasonable formulation for
the internal extinction within galaxies, provided that they are
optically thin. Surface photometry data over a broad wavelength range
would greatly help to clarify the values of f and  , particularly any dependence on
morphological type for these parameters.
, particularly any dependence on
morphological type for these parameters.
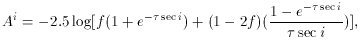
 is the optical
depth. The additional parameter
f is the fraction of the light that is unobscured by the dust
layer. Thus, f = 0.5 leads to the infinitely thin layer model, while
f = 0 leads to the model proposed by Holmberg.
Tully and
Fouqué (1985)
adopted
is the optical
depth. The additional parameter
f is the fraction of the light that is unobscured by the dust
layer. Thus, f = 0.5 leads to the infinitely thin layer model, while
f = 0 leads to the model proposed by Holmberg.
Tully and
Fouqué (1985)
adopted  ~ 0.55 for the
B band, f ~ 0.25, and
suggested that the data are better fit if the extinction for i >
80° is held at the value for 80°. At present, this simplistic
two-component model appears to be the most reasonable formulation for
the internal extinction within galaxies, provided that they are
optically thin. Surface photometry data over a broad wavelength range
would greatly help to clarify the values of f and
~ 0.55 for the
B band, f ~ 0.25, and
suggested that the data are better fit if the extinction for i >
80° is held at the value for 80°. At present, this simplistic
two-component model appears to be the most reasonable formulation for
the internal extinction within galaxies, provided that they are
optically thin. Surface photometry data over a broad wavelength range
would greatly help to clarify the values of f and  , particularly any dependence on
morphological type for these parameters.
, particularly any dependence on
morphological type for these parameters.


