


8.2 The Planetary-Nebula Luminosity Function
In his study of Magellanic Cloud planetaries,
Jacoby (1980)
showed that the
[O III]  5007 luminosity
function for faint planetaries is well
represented by an exponential law formed by combining a uniformly expanding
shell with a non-evolving central star
(Henize and
Westerlund 1963).
However, as the CCD observations of PN in M31
(Ciardullo et
al. 1989),
M81
(Jacoby et
al. 1989),
the Leo I Group
(Ciardullo et
al. 1989),
the NGC 1023 Group
(Ciardullo et
al. 1991), the Magellanic Clouds
(Jacoby et al. 1990),
and Virgo
(Jacoby et al. 1990)
have shown, the bright end of this function is
truncated rather dramatically, in a manner similar to that predicted by the
theoretical models of
Jacoby (1989).
Ciardullo et
al. (1989)
therefore modified the Henize and Westerlund law by adding a cutoff
exponential, proposing that
5007 luminosity
function for faint planetaries is well
represented by an exponential law formed by combining a uniformly expanding
shell with a non-evolving central star
(Henize and
Westerlund 1963).
However, as the CCD observations of PN in M31
(Ciardullo et
al. 1989),
M81
(Jacoby et
al. 1989),
the Leo I Group
(Ciardullo et
al. 1989),
the NGC 1023 Group
(Ciardullo et
al. 1991), the Magellanic Clouds
(Jacoby et al. 1990),
and Virgo
(Jacoby et al. 1990)
have shown, the bright end of this function is
truncated rather dramatically, in a manner similar to that predicted by the
theoretical models of
Jacoby (1989).
Ciardullo et
al. (1989)
therefore modified the Henize and Westerlund law by adding a cutoff
exponential, proposing that
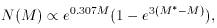 (18)
(18)
where the magnitude, M, is related to the  5007 flux of a planetary
by
5007 flux of a planetary
by
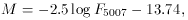 (19)
(19)
and M* is the absolute magnitude for the most luminous planetary.
To set the zero point of the function,
Ciardullo et
al. (1989)
used 104 unobscured PN in the bulge of M31. By adopting the infrared Cepheid distance
of 710 kpc
(Welch et al. 1986),
and a total foreground extinction of
A5007 = 0.39, Ciardullo et al. found the best fit
value for M* to be
M* = -4.48 with a 1 internal
error of +0.036, -0.046. Because
these 104 PN serve as the sole absolute calibrator for PNLF distances, this
internal error, as well as the external uncertainty in M31's true distance
and reddening, propagates directly into all subsequent PNLF measurements.
Future observations may reduce the internal error by enlarging the sample of
PN used in the calibration, but because PN are secondary standard candles,
PNLF distances will always be subject to uncertainties in the Local Group
distance scale. In fact, recent estimates for M31's distance (770 kpc;
Freedman and Madore
1990)
and reduced extinction (A5007 = 0.28;
Burstein and Heiles
1984)
suggest a cutoff that is 0.06 mag more luminous.
internal
error of +0.036, -0.046. Because
these 104 PN serve as the sole absolute calibrator for PNLF distances, this
internal error, as well as the external uncertainty in M31's true distance
and reddening, propagates directly into all subsequent PNLF measurements.
Future observations may reduce the internal error by enlarging the sample of
PN used in the calibration, but because PN are secondary standard candles,
PNLF distances will always be subject to uncertainties in the Local Group
distance scale. In fact, recent estimates for M31's distance (770 kpc;
Freedman and Madore
1990)
and reduced extinction (A5007 = 0.28;
Burstein and Heiles
1984)
suggest a cutoff that is 0.06 mag more luminous.
Since the Ciardullo et al. PNLF is not a power law, and, in fact, shows a rapid
decline over the brightest magnitude of the luminosity function, a fit of the
observed PNLF to equation (18) yields a distance directly, provided, of course,
that the function is invariant. Fortunately, there is good evidence to show
that this function, if not invariant, is at least insensitive to galaxy color,
metallicity, or Hubble type. Well defined PNLFs currently exist for 17 giant
spiral, elliptical, and irregular galaxies. In none of these objects is
there any evidence for a change in the shape of the PNLF cutoff
(cf. Figure 15).
More importantly, the zero point of this function also appears to be constant.
In the Leo I Group,
Ciardullo et
al. (1989)
found that the PNLF
distances for three elliptical and S0 galaxies, NGC 3377, 3379, and 3384,
all fell within 0.5 Mpc, or 5%, despite the fact that the galaxies differ by
0.8 mag in absolute luminosity,
0.3 mag in (U - V) and 0.1 in [Fe/H].
Jacoby et al. (1990)
derived a similar result for six early-type galaxies in the
Virgo Cluster core:
although the galaxies span a range of 0.19 in [Fe/H], 0.22 mag in (U
- V),
and 2.2 mag in (m1550 - V), the 1 dispersion in their computed
distances was again only 5% (0.8 Mpc). Perhaps the strongest internal
confirmation of the insensitivity of the PNLF to stellar population, however,
comes from the agreement between the PNLFs of NGC 1023, a gas-rich S0 galaxy,
and fellow group member NGC 891, the edge-on Milky Way lookalike.
Ciardullo et
al. (1991)
measured identical distances to these two galaxies,
using as their data a complete sample of PN in NGC 1023's disk and NGC 891's
halo. Since the halo stars of NGC 891 are undoubtably much older than the disk
objects of NGC 1023 (NGC 1023 formed stars ~ 3 Gyrs ago
[Gregg 1989]),
this result strongly supports the contention that a galaxy's star formation
history does not play an important role in determining the PNLF cutoff.
Moreover, since the total number of PN found in NGC 891's halo is a factor of
three less than that discovered in NGC 1023, the similarity in the derived
distances to these two galaxies is additional evidence that the PNLF cutoff
is indeed an exponential, rather than a power law as proposed by
Bottinelli et
al. (1991).
dispersion in their computed
distances was again only 5% (0.8 Mpc). Perhaps the strongest internal
confirmation of the insensitivity of the PNLF to stellar population, however,
comes from the agreement between the PNLFs of NGC 1023, a gas-rich S0 galaxy,
and fellow group member NGC 891, the edge-on Milky Way lookalike.
Ciardullo et
al. (1991)
measured identical distances to these two galaxies,
using as their data a complete sample of PN in NGC 1023's disk and NGC 891's
halo. Since the halo stars of NGC 891 are undoubtably much older than the disk
objects of NGC 1023 (NGC 1023 formed stars ~ 3 Gyrs ago
[Gregg 1989]),
this result strongly supports the contention that a galaxy's star formation
history does not play an important role in determining the PNLF cutoff.
Moreover, since the total number of PN found in NGC 891's halo is a factor of
three less than that discovered in NGC 1023, the similarity in the derived
distances to these two galaxies is additional evidence that the PNLF cutoff
is indeed an exponential, rather than a power law as proposed by
Bottinelli et
al. (1991).
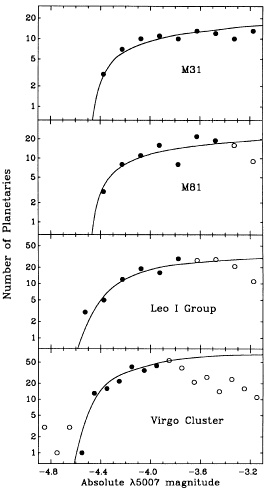
Figure 15. The observed planetary-nebula luminosity functions for
M31, M81, three galaxies in the Leo I group, and six
galaxies in the
Virgo cluster. Aside from small differences caused
by the photometric
errors associated with each observation, the shapes of the four
functions are identical, demonstrating the form of the PNLF does not
depend on Hubble type. Open circles display points which were not used
in the solution. The solid lines show the best empirical luminosity
functions.
|
External comparisons have also proved that PNLF distances do not depend
strongly on the properties of the underlying stellar population. PNLF
surveys in the bulge of the Sb galaxy M81 and in the Large Magellanic Cloud
have resulted in derived distances to these galaxies
(Jacoby et al. 1989;
Jacoby et al. 1990)
that are statistically indistinguishable
from that found from the I-band and infrared observations of Cepheids
(cf.
Freedman and Madore
1988;
Welch et al. 1987;
Feast and Walker
1987).
Moreover,
Pottasch's (1990)
PNLF based estimate of 8.1 kpc for the distance to
the Galactic Center is completely consistent with that determined by other
methods
(Reid 1989).
Finally, it should be noted that the PNLF distances to
the Leo I, NGC 1023, and Virgo clusters are in excellent agreement with
those estimated from the Tully-Fisher method
(Pierce and Tully
1989;
Aaronson and Mould
1983),
and a comparison between the PNLF and surface brightness
fluctuation distances for 14 galaxies measured by both methods yields a
dispersion of only 0.19 mag, a number consistent with the
internal error estimates of the two methods (see
Sec. 11).



 5007 luminosity
function for faint planetaries is well
represented by an exponential law formed by combining a uniformly expanding
shell with a non-evolving central star
(Henize and
Westerlund 1963).
However, as the CCD observations of PN in M31
(Ciardullo et
al. 1989),
M81
(Jacoby et
al. 1989),
the Leo I Group
(Ciardullo et
al. 1989),
the NGC 1023 Group
(Ciardullo et
al. 1991), the Magellanic Clouds
(Jacoby et al. 1990),
and Virgo
(Jacoby et al. 1990)
have shown, the bright end of this function is
truncated rather dramatically, in a manner similar to that predicted by the
theoretical models of
Jacoby (1989).
Ciardullo et
al. (1989)
therefore modified the Henize and Westerlund law by adding a cutoff
exponential, proposing that
5007 luminosity
function for faint planetaries is well
represented by an exponential law formed by combining a uniformly expanding
shell with a non-evolving central star
(Henize and
Westerlund 1963).
However, as the CCD observations of PN in M31
(Ciardullo et
al. 1989),
M81
(Jacoby et
al. 1989),
the Leo I Group
(Ciardullo et
al. 1989),
the NGC 1023 Group
(Ciardullo et
al. 1991), the Magellanic Clouds
(Jacoby et al. 1990),
and Virgo
(Jacoby et al. 1990)
have shown, the bright end of this function is
truncated rather dramatically, in a manner similar to that predicted by the
theoretical models of
Jacoby (1989).
Ciardullo et
al. (1989)
therefore modified the Henize and Westerlund law by adding a cutoff
exponential, proposing that



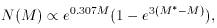
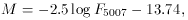
 internal
error of +0.036, -0.046. Because
these 104 PN serve as the sole absolute calibrator for PNLF distances, this
internal error, as well as the external uncertainty in
internal
error of +0.036, -0.046. Because
these 104 PN serve as the sole absolute calibrator for PNLF distances, this
internal error, as well as the external uncertainty in 