8.3 Method

The identification and accurate measurement of planetary nebulae in external galaxies requires special care which begins with the selection of the narrow band filter. The best way to image PN in distant galaxies is through an interference filter with a full-width-half-maximum bandpass of ~ 30 Å. (Filters much narrower than ~ 25 Å may suppress planetaries which are redshifted onto the filter wings by the velocity dispersion of the galaxy. Broader filters, however, admit too much continuum light from the host galaxy and degrade the signal-to-noise.) Unfortunately, observations of emission line sources are difficult to calibrate photometrically, and the narrowness of the filter compounds the problem. In order to compare the flux of an emission line object with that of a continuum source (e.g., a standard star), the transmission of the filter at the wavelength of the emission line must be compared to the filter's mean transmission (Jacoby et al. 1987). This presents a problem, since the properties of a narrow band filter change with temperature and illumination angle. In particular, a drop in temperature will cause a filter to shift its bandpass to the blue, while fast optics will lower a filter's peak transmission and drastically alter the shape of the transmission curve (Eather and Reasoner 1969). These effects limit the accuracy of PN flux measurements made with a fast beam (e.g., the prime focus of the KPNO and CTIO 4-m telescopes) to a few percent. A complete discussion detailing the difficulties and calibration procedures for narrow band filters appears in Jacoby et al. (1989).

While the selection and calibration of an appropriate narrow band filter may be difficult, identifying and measuring planetary nebulae on a CCD frame is relatively easy. PN are visible on 5007 frames but are completely invisible on comparably deep off-band frames. Thus, by ``blinking'' the two images, planetary nebulae can be found almost immediately. Unfortunately, it is sometimes difficult to measure faint PN superposed on a bright, rapidly varying background of a galaxy. One method of handling this problem is to use a low order polynomial to flatten the sky around each object prior to photometry. A more effective technique, which is particularly useful in the bright inner regions of galaxies, is to create a ``difference'' picture. In this procedure, an off-band image taken through a filter adjacent to 5007 is scaled to, then subtracted from the on-band frame, until the background continuum disappears. What is left, aside from the imperfect subtractions of foreground stars, are isolated images of emission line sources, which can then be measured with either aperture photometry or point-spread-function fitting techniques (cf. Figure 16). This differencing technique works best if the read noise of the detector is low. Unlike broadband observations for stars in distant galaxies, narrow band PN images are not always sky noise limited; hence the subtraction of poor signal-to-noise frames increases the photometric errors. For modern low noise detectors, however, this additional error is small, and is more than compensated for by the precision of the flattened background (cf. Jacoby et al. 1990).

Figure 16. Difference images are effective tools for identifying faint planetary nebulae in distant galaxies. Displayed is small section of a halo field in M81 obtained with the KPNO 4-m telescope and a TI CCD. The top left-hand panel shows the frame in the light of redshifted 5007, the top right-hand panel shows an offband 5250 image, and the bottom panel displays the scaled difference between the two images. A bright planetary and two fainter ones are easily visible on the difference frame.

Once the PN of a galaxy have been identified and measured, their distance can be obtained by comparing their luminosity function to that of M31, as represented by equation (18). This can best be done using the method of maximum likelihood (Ciardullo et al. 1989). An analysis of this type, however, requires a proper statistical sample of PN and an appropriate model for the empirical function. Unsharp masks and color maps may be used to exclude objects affected by internal extinction, but a more serious issue concerns the inclusion of objects near the frame limit. Because the detectability of planetary nebulae varies with background surface brightness, the selection of a homogeneous sample of objects requires knowing how the limiting PN magnitude changes with position in the galaxy. Fortunately, Renzini and Buzzoni (1986) have shown that the luminosity specific stellar death rate for a stellar population is insensitive to the population's age, initial mass function, and metallicity. Hence, the probability of finding a planetary nebula at any location within a galaxy should be roughly proportional to the galaxy's surface brightness at that location. Observations in M31, M81, Leo I, and Virgo confirm this conclusion, and offer a direct and simple method of statistically validating a sample of PN candidates. Since the distribution of PN should follow the bolometric light of the host galaxy, if the two distributions disagree, then the sample of PN is either contaminated by the inclusion of spurious images, or, more likely, reduced by incompleteness.

If the PN identifications are found to be incomplete, two alternatives are available: one can either use all the data and correct for the incompleteness, or one can restrict the sample to a subset of objects which is complete. The former option is difficult and tedious, and introduces an unnecessary uncertainty. Since PN measurements must be made within the body of the galaxy, the correction factors which are needed depend both on the apparent PN magnitude and the background surface brightness. Procedures which attempt to measure these factors must therefore be two dimensional in nature and involve a large number of simulations. Fortunately, for most applications, such complex models are not needed. Unlike the globular cluster luminosity function, whose accurate measurement requires observations as far past the turnover as possible, PNLF distances depend more on the photometry of the brightest objects than the faintest. Thus, while faint PN do contribute to the fit, accurate (~ 10%) distances can be obtained with PN measurements that extend only ~ 1 mag down the luminosity function. This being the case, a simple and straightforward method exists for defining a homogeneous set of planetaries. To create a complete sample, one needs only compare the distribution of PN with that of the galaxy light for samples of objects with differing limiting magnitudes. When the two distributions agree, the PN sample can be considered complete (Ciardullo et al. 1989).

After defining the PN sample, the information most needed for modeling the PNLF is some knowledge of how the photometric error varies with magnitude. Since the observed PNLF should be the convolution of the universal PNLF with the photometric error function, this correction, if ignored, can lead to an underestimation of the true distance (Ciardullo et al. 1989). Similarly, if a PNLF survey is conducted in the central regions of a distant galaxy and the model luminosity function does not provide for the occurrence of chance PN superpositions, then the true distance will again be underestimated (Jacoby et al. 1990). Under most circumstances, however, these factors only change the derived distance to a galaxy by a few percent, and, if appropriate care is taken with the photometric measurements and the modeling of PN superpositions, neither effect should be important.

Thus far, PN have been used primarily for early type galaxies. The major reason for this is the possible contamination of the PNLF by compact H II regions. In their survey of M81's bulge, Jacoby et al. (1989) discriminated between PN and H II regions by requiring that all PN be stellar and have an [O III] 5007 to H ratio much greater than one. The theory behind this is that PN central stars are much hotter than typical OB associations, and their nebulae have much higher excitation temperatures. Unfortunately, some H II regions, such as NGC 2363 in NGC 2366 (Kennicutt et al. 1980) do have high [O III]-to-H ratios and at large distances, objects such as these can be confused with planetaries (Ciardullo et al. 1991). For early-type galaxies with few H II regions, the probability of seeing one of these high excitation objects is small, and, unless the object has an absolute 5007 magnitude within ~ 0.2 mag of M*, its misidentification will not significantly alter the derived distance. (An H II region that is much brighter than M* can be statistically excluded from the sample on the basis of its deviation from the empirical law. Faint interlopers, on the other hand, are numerically unimportant compared to the population of true PN.) However, in late-type spiral and irregular galaxies, where the total number of H II regions far exceeds the number of bright planetaries, these [O III] bright regions can distort and possibly overwhelm the PNLF. The only way to positively discriminate between H II regions and planetary nebulae in these galaxies is by size - planetary nebulae further than ~ 2 Mpc away will always appear stellar, even with a diffraction-limited Hubble Space Telescope. H II regions, on the other hand, are usually larger than ~ 20 pc across, and one can hope to resolve them even at distances as large as ~ 15 Mpc. To do this, PNLF measurements in late-type galaxies must be performed from space, or from a ground-based telescope capable of high spatial resolution.

When an empirical model is compared with an uncontaminated sample of planetaries, two independent variables are fit: the distance modulus, µ, and the total PN population, N. For understanding the three dimensional distribution of galaxies, the distance modulus is, of course, the more important parameter, but the latter quantity is of considerable interest from an astrophysical standpoint. When the total number of planetaries is normalized to bolometric luminosity, the result is the luminosity specific PN density, a quantity which is closely related to the population's evolutionary flux and the specific stellar death rate. As mentioned above, Renzini and Buzzoni (1986) have shown theoretically that the luminosity specific stellar death rate should be insensitive to a population's age, metallicity, or initial mass function. However, the PNLF analyses to date suggest that the rate of PN production correlates with (U - V) index, in the sense that blue galaxies produce more PN per unit luminosity than galaxies with a redder population (Peimbert 1990; Ciardullo et al. 1991; Richer and McCall 1992). If this preliminary result holds true, then this PNLF by-product will be an important tool for helping us to understand the late stages of stellar evolution.

Figure 17 displays contours of probability in distance modulus and PN density for the observed PNLF of the elliptical galaxy NGC 4406 in the Virgo Cluster. This result, which is based on a homogeneous sample of 59 PN extending 0.7 mag down the luminosity function, is typical of what is possible with a 3 hour 5007 exposure on a 4-m telescope, with 1" seeing and a low noise, blue-sensitive CCD. The displayed 1 contour corresponds to an uncertainty of +0.051, -0.059 mag. However, these contours only reflect the formal internal precision of the fitting procedure. The true error of any PNLF distance determination also includes uncertainties in the standard star measurements and filter calibration (~ 0.05 mag), the foreground extinction to the galaxy (~ 0.05 mag), the definition of M* (~ 0.04 mag), and the distance and extinction to the calibration galaxy, M31 (0.10 mag). Hence, although the precision of NGC 4406's measurement is 0.06 mag, the true error in its distance modulus is closer to 0.14 mag.

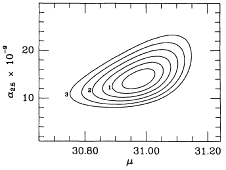
Figure 17. Probability contours derived from the method of maximum likelyhood applied to a homogeneous sample of 59 PN in the Virgo cluster elliptical galaxy NGC 4406. The abscissa is the true distance modulus; the ordinate represents the number of PN within a 2.5 mag of the magnitude cutoff M*, normalized to the amount of bolometric luminosity surveyed. The contours of probability (shown at intervals of 0.5) arise from the uncertainty in fitting the model PNLF to the observed luminosity function: horizontal errors reflect the uncertainty in fitting the distance modulus, while vertical errors come from uncertainties in normalizing to the observed number of PN.

Implicit in the likelihood contours of Figure 17 is the assumption that the empirical form of the PNLF, as given in equation (18) is correct. Because Bayesian statistical methods only compare probabilities, the solutions which arise from likelihood analyses must also be checked with a ² or Kolmogorov-Smirnov (hereafter referred to as KS) test. If a best fit empirical law is excluded by such a test, then the maximum likelihood solution must be discarded. Conversely, any alternative law that does not pass a ² or KS test cannot be considered viable. It is, in fact, on this basis that a power law PNLF cutoff proposed by Bottinelli et al. (1991) can be rejected at the 5 level.

As with all stellar-based standard candles, the usefulness of the PNLF method is limited by the size of the telescope, the brightness of the background sky, and, most importantly, by the image quality. With 0."5 seeing on a dark night, a 4-m class telescope can measure PN as faint as m₅₀₀₇ ~ 28.9 in ~ 3 hours. Thus, in theory, galaxies as far away as ~ 30 Mpc can be measured with today's telescopes. In practice, however, the true limit of the PNLF technique is slightly less than this, due to background luminosity of the host galaxy and the limitations of variable seeing over long exposures. Nevertheless, clusters such as Crater, Pavo-Indus, and even the lower-redshift component of the Centaurus Cluster, which stands half-way between us and the Great Attractor (Lucey et al. 1986; Burstein et al. 1990), should all be measurable with current instrumentation via the PNLF technique.