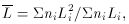An image of an elliptical galaxy with milli-arcsec resolution would look like an enormous globular cluster, but even when the resolution is a thousand times worse, the discreteness of the stars causes measurable bumpiness in its surface brightness. This phenomenon, dubbed ``surface brightness fluctuations'', has been recognized for many years and is sometimes referred to as ``incipient resolution''. (When there are only a few stars per seeing resolution element, the eye perceives this characteristic mottling as barely resolved stars.)
Observations of external galaxies from which fluxes could be determined for individual stars, drawn from a significant part of the stellar luminosity function, would provide us a wealth of information about the distances of galaxies, their stellar populations, and their formation history. The first steps in this direction were taken by Baade (1944), who first resolved individual Pop II stars in Local Group galaxies, and Baum and Schwarzschild (1955) who observed the top of the luminosity function in the bulge of M31 and NGC 205. Improvements of this work include papers by Mould et al. (1983, 1984), by Pritchet and van den Bergh (1988), and by Freedman (1989). However, the resolution required to observe any but the most luminous stars in galaxies significantly beyond the Local Group will not be achieved in the near future.
Although we cannot determine the fluxes of individual stars without resolving them, we can nevertheless measure a very useful flux that is characteristic of the stellar population. This effect was quantitatively discussed in another context by King (1966) who realized that average profiles of globular clusters could best be determined at the bluest wavelengths where these fluctuations are minimized. Baum (1986, 1990) has investigated the possibility of measuring fluctuation amplitudes by examining the histogram of pixel amplitudes.
The first measurement of surface brightness fluctuations was by
Tonry and Schneider
(1988),
who described a method by which
the fluctuations could be quantified. Subsequent papers include
Tonry et al. (1988)
which gives additional observations and revised analysis technique,
Tonry et al. (1989)
which is a first report on 1989 observations
of Virgo galaxies using the KPNO 4-m telescope,
Tonry et al. (1990)
which provides a final analysis of those
Virgo observations and describes improved analysis
methods, and
Tonry and Schechter
(1990)
who report on fluctuation observations of
NGC 5128.
Tonry (1991)
discusses a completely empirical calibration
of fluctuation absolute magnitudes, observations of four galaxy clusters,
and the application of fluctuations to the distance scale.
Note that the distances in the papers prior to 1991 all need to
be corrected to the new, empirical calibration for
| 
|
Figure 18. The schematic galaxy at the right-hand side is twice
as distant as the one on the left-hand side. Large dots symbolize giant
stars, small ones main-sequence stars, and the grid represents the
pixels of a CCD. Although the mean surface brightness collected in a CCD
pixel is the same for the two galaxies, since f  d-2 and
n
d2, the rms fluctuation from pixel to pixel relative
to the mean varies as d-1. The image at the left is
about as mottled as an I-band image of a real galaxy would be at
its effective radius if the galaxy were 200 kpc distant and the scale of
CCD pixels were 1".
| |
Surface brightness fluctuations are fundamentally a very simple effect, and Figure 18 illustrates this with a cartoon of two galaxies, one twice as distant as the other. A grid representing a CCD's pixels is superposed on the images, and we must imagine that we can only measure the total flux within each pixel. We do not resolve individual stars in this case, but we can measure both the mean flux per pixel and the rms variation in flux from pixel to pixel. The two galaxies cannot be distinguished on the basis of mean flux per pixel (surface brightness) because the number of stars projected into a pixel of fixed angular size increases as distance squared (d2) and the flux per star decreases as d-2. If N is the mean number of stars, the mean flux is N fbar, and the variance in flux is N fbar2, where fbar is a mean flux per star. In Figure 18, N scales as d2, fbar scales as d-2, and so the variance scales as d-2 and the rms scales as d-1. The galaxy which is twice as distant appears twice as smooth as the nearer galaxy. We can now determine the mean flux fbar as the ratio of the variance and the mean.
The mean luminosity, Lbar is simply related to the moments of the luminosity function of the stellar population we are sampling. If ni is the expectation of the number of stars of luminosity Li, the average luminosity is the ratio of the second and first moments of the luminosity function:
(Tonry and Schneider 1988). This luminosity is roughly that of a giant star, and it is the first ratio of moments which has the dimensions of luminosity and is not dominated by the poorly known faint end of the luminosity function.