9.2 Method

There are two aspects to determining a distance from surface brightness fluctuations: (1) measurement of a fluctuation flux, and (2) conversion to a distance by assumption of a fluctuation luminosity. The two are coupled, but it is worth discussing them separately because they involve very different problems. It is useful to bear in mind that for typical old, metal rich stellar populations the absolute fluctuation magnitudes are roughly barM_B = +2.5, barM_V = +1.0, barM_R = +0.0, and barM_I = -1.5, with sensitivity to metallicity and age ranging from very high in B to fairly low in I. The results which are discussed in detail below can be summarized as:

(1) This method is applicable to relatively dust-free systems such as E and S0 galaxies, spiral bulges, or globular clusters.

(2) Observation times must be long enough to collect more than 5-10 photons per source of apparent magnitude barm, and the point spread function must be well sampled and uniform. The formal measurement errors in barm can be as small as 3% times the square of the product of psf FWHM (in arcsec) and distance (in 1000 km s^-1).

(3) The I band is preferred for distance measurement because barM is so bright at redder wavelengths that it overcomes the disadvantages of brighter sky background. Use of the I band also minimizes dust absorption. Observations of cluster galaxies shows us how barM_I depends on mean color: redder populations have brighter barM_I. The intrinsic scatter of barM_I about this relation appears to be smaller than 0.08 magnitude.

(4) Calibration of the zero point of barM_I can be based on theoretical stellar populations, galactic globular clusters, or Local Group galaxies. The latter calibration has been made, and preliminary indications are that the first two will be consistent at the 0.10 magnitude level.

The basic procedure in measuring a fluctuation flux is to perform the usual observations and reductions so as to obtain an image which is as flat and uniform as possible and for which a photometric calibration is known.

The fluctuation signal grows proportional to time, since we are observing real (albeit statistical) lumps in the galaxies. If we observe long enough to collect several (ideally 10 or more) photons per giant star, we have passed the regime of being dominated by photon counting statistics into a regime where we are dominated by star counting statistics. Thus the observation time required is independent of the size of a galaxy, and in the absence of sky background, all points in a galaxy would simultaneously have the same ratio of fluctuation variance to photon counting variance. If the ratio of sky to galaxy brightness is significant, the number of photons collected per barm should be increased by one plus that ratio.

We then essentially measure an average flux and an average variance in some region and get a fluctuation flux barf from the ratio of the two. There are a number of complications: (1) there are many other contributors to variance besides the Poisson statistics of the number of stars present, (2) the image has been smeared by a point spread function (psf) which affects the variance, (3) there is a possibility of the image being mottled or dimmed by dust obscuration, and (4) the assumption that adjacent pixels are independent samples of a stellar population may be compromised by intrinsic correlations such as spiral arms. The details of the measurement are described in Tonry et al. (1990), but some points will be reiterated in order to evaluate the strengths and weaknesses of the method.

Apart from star counts, variance in an image gets contributions from CCD flaws such as traps and bad columns, CCD read noise, and residual flattening problems of CCD images. In addition, each pixel carries Poisson noise from the number of photons collected from the source. Variance also arises from cosmic rays, foreground stars, and background galaxies scattered across the image, and lumps intrinsic to the galaxy being observed such as globular clusters and spiral arms. Patchy obscuration can modulate the flux from the galaxy and create variance, and smooth obscuration can reduce the variance which we measure and hence the flux we derive.

By restricting ourselves to clean E and S0 galaxies we can minimize problems with patchy dust obscuration, but fluctuations can also be measured in spiral galaxies with large bulges, provided that there is sufficient resolution in a blue enough band to determine which regions are contaminated by dust. M31 and M81, for example, have patchy obscuration throughout their bulge. Failure to excise the dust patches which are visible in V band images of those systems results in an I band variance which is 10-20% larger than when the obvious patches are removed. Presumably when the obvious patches have been removed there is negligible power from the remaining obscuration, although this has yet to be tested by using bluer wavelengths or better seeing.

Another advantage accruing from early-type galaxies (or bulges) is that their velocity dispersions are so high that only very dense lumps such as globular clusters survive, and there are negligible pixel-to-pixel correlations from gravitational clumping.

The method by which we discriminate against these unwanted sources of variance is to subtract a smooth fit to the galaxy, remove all areas contaminated by CCD flaws, point sources, and dust, and then measure the variance from the Fourier power spectrum. This has an additional advantage that the zero-wavenumber limit of the power spectrum is the power in the image before it was convolved with the psf. Read noise, cosmic rays, and photon statistics all have a white power spectrum which can be distinguished from the power spectrum of fluctuations, stars, globular clusters (GCs), and background galaxies, which have the power spectrum of the psf. The GCs and galaxies remaining in an image at the excision limit are so poorly resolved that there is negligible difference between their power spectrum and that of the psf. Most of the power from patchy obscuration and poor flattening occurs on scales which are very different from the psf and, affecting mainly very low wavenumbers, disturb the fluctuation measurement only slightly.

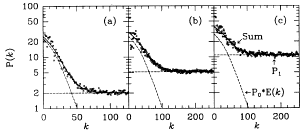
Figure 19. Azimuthal averages of power spectra from the following three regions og NGC 4552 in the I band: (a) annulus with an inner radius of 64 and an outer radius of 128 pixels, (b) annulus with radii 128 and 256, (c) southeast quadrant of an annulus with radii 256 and 400. The data points are plotted along with the fit to the data and the two components of the fit, P0 x E(k) and P1, where E(k) is the expectation power spectrum for unity fluctuation power. All are scaled by E(0); P0 is approximately 25 e- (i.e., each source of apparent magnitude barmI contributes about 25 e- during this 1024-s exposure on the KPNO 4-m telescope). P0 increases slightly with radius as Pr increases; the P1 component increases with radius as the ratio of the sky to galaxy increases.

Figure 19 illustrates a power spectrum. The model fitted to the data consists of a constant P₁ (from the white noise component) plus another constant P₀ multiplying the power spectrum of the psf, determined from stars in the image. There is clearly extra noise at very low wavenumbers, but there is a substantial range of wavenumbers where P₀ is very tightly constrained by the data. The fluctuation variance in the image depends on the product of barf and the mean galaxy flux; we prefer to scale Figure 19 by this mean flux so that the power plotted as the ordinate gives us barf directly in detected photons.

The P₀ component of the variance has contributions P_flux from fluctuations and P_r from point sources remaining in the image. Use of an automated photometry program permits us to find all point sources in the image to some completeness level, excise all objects brighter than that level, and then examine the luminosity function to estimate P_r. If we fit a model to the observed luminosity function which allows for stars, globular clusters, and background galaxies, we can consistently estimate P_r with an accuracy of about 20% from the integrated variance of the model beyond the excision limit. This procedure is illustrated in Figure 20.

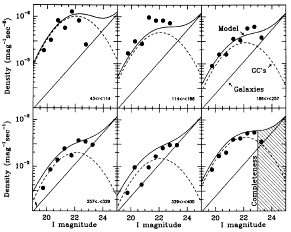
Figure 20. Luminosity functions of objects in the I image of NGC 4552 in annuli of different radius. Each panel shows as a function of magnitude the observed number density, the model number density, and its two components, globular clusters and nackground galaxies. The lower right-hand panel shows the luminosity function over the entire area of the image analyzed (although the analysis uses the radially dependent model), and a possible value for mlim is indicated by the completeness line.