Copyright © 1981 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1981. 19:
373-410 Copyright © 1981 by Annual Reviews. All rights reserved |
6.3 Interpretation of Superluminal Motion
Attempts to understand the superluminal motion have produced a flurry of imaginative phenomenological interpretations including
(a) real tachyonic motion;
(b) grossly incorrect Hubble constant or non-cosmological red shifts (Kellermann & Shaffer 1977, Burbidge 1978) or incorrect cosmological model (Segal 1979);
(c) light echoes (Lynden-Bell 1977, Lynden-Bell & Liller 1978);
(d) gravitational lenses and screens (Barnothy & Barnothy 1971, Chitre & Narlikar 1980);
(e) systematic variations in synchrotron opacity (Epstein & Geller (1977);
(f) synchrotron or curvature radiation from electrons gyrating in a fixed dipole field (Milgrom & Bahcall 1978, Sanders & Da Costa 1978, Bachall & Milgrom 1980);
(g) various kinematic illusions caused by the finite signal propagation time (Rees 1966, 1967, Cavaliere et al. 1971).
It is beyond the scope of this paper to discuss all of these models in any detail. In general, they each explain some but not all of the observed characteristics of motion and, with the exception of the last category, are not supported by the other observational data discussed in previous sections. For a complete discussion of the various models see Rees (1971, 1978), Blandford, McKee & Rees (1977), Blandford & Rees (1978), Blandford & Konigl (1979), and Marscher & Scott (1980).
In this review we concentrate on interpretations based on bulk relativistic motions. The first suggestion that this effect might be important in compact radio sources was made by Rees (1966, 1967) well before the observational discovery of superluminal motion. Rees postulated relativistically expanding sources to explain the observed rapid flux density variations (Rees & Simon 1968), but more detailed studies have since shown that short flux density outbursts cannot be satisfactorily explained in this way (Terrell 1977, Jones & Tobin 1977, Vitello & Pacini 1978). However, relativistic linear motion, which is oriented nearly along the line of sight, does lead to a satisfactory explanation of the rapid flux density outbursts, as well as the observed superluminal component motion.
Due to the finite propagation time of the signal radiated, the time
scale for events seen by an external observer at rest with respect to
an approaching source is shortened by a factor
~  -1.
(3) Thus the apparent
angular size deduced from light-travel-time arguments is too small by
a factor of
-1.
(3) Thus the apparent
angular size deduced from light-travel-time arguments is too small by
a factor of  , and
the corresponding brightness temperature too great
by a factor of
, and
the corresponding brightness temperature too great
by a factor of
 2.
Values of
2.
Values of  ~ 10
(
~ 10
( ~ 0.995) are generally
adequate
to reduce the apparently excessive brightness temperatures discussed
in Section 4.2, although for some of the low
frequency variables, uncomfortably high values
~ 0.995) are generally
adequate
to reduce the apparently excessive brightness temperatures discussed
in Section 4.2, although for some of the low
frequency variables, uncomfortably high values
 ~ 100
(
~ 100
( ~ 0.9999) may be needed.
~ 0.9999) may be needed.
The apparent transverse velocity
v of an
object moving with a true
velocity v is given by
(Ginzburg &
Syrovatskii 1969):
of an
object moving with a true
velocity v is given by
(Ginzburg &
Syrovatskii 1969):
where
which is observed no matter how great the true space velocity. For
small values of
These results are only slightly changed if we consider two objects
moving in opposite direction from a common origin. Then the velocity
of separation
vs
which has a maximum velocity at an angle sin
The two cases, of oppositely directed ejection of two components,
and ejection of a single component seen together with a stationary
core, could be distinguished by measuring the "absolute" component
positions by comparison with nearby (stationary) reference
sources. Differential position measurements of the required accuracy
are possible with VLB techniques
(Shapiro et al. 1979).
Also, high
resolution maps made with sufficient dynamic range can determine the
number of components and their relative motion.
The probability, P(
An important consequence of the bulk relativistic motion is that the
radiation is no longer isotropic but is beamed along the direction
motion within an angle of halfwidth ~
1/
when viewed at angle
For an approaching component viewed "head-on," and
while the receding component (cos
A detailed description of the appearance, time variations, and
spectral behavior of two sources separating with relativistic velocity
is given in the classical paper by
Ozernoi & Sazonov
(1969),
which preceded the observational discovery of superluminal motion. With
great perception Ozernoi & Sazonov were able to infer the double
relativistic ejection from consideration of the radio source spectra
and total flux variations alone.
The interpretation of the observed superluminal motion in terms of
bulk relativistic motion is very attractive in that it avoids the need
to resort to non-cosmological red shifts or to abandon the synchrotron
radiation mechanism: at the same time it provides a natural
interpretation for the rapid flux density variations, the absence of
inverse Compton scattered X rays, and interstellar scintillations, as
well as the general asymmetric appearance of the superluminal sources.
The models also fit naturally into the general picture of
extragalactic radio sources in which energy is thought to be supplied
to the extended lobes by means of well-collimated beams or jets
(Blandford & Rees 1974,
Scheuer 1974,
DeYoung 1976,
Miley 1980,
Fomalont 1981).
Nevertheless, the large bulk velocities of
(a) While the apparently excessive energy requirement in the form of
relativistic particles is greatly reduced, the reduction is at the
expense of energy that is tied up in component motion and in the
magnetic field.
(b) The superluminal radio sources are smaller than the probable
dimensions of the excited clouds of gas that give rise to the narrow
optical emission lines. It is normally assumed that the radio source
lies at least within the emission line region, so that, depending on
the energy in the relativistic component,
Jones & Burbidge (1973)
argue that either it should be slowed down to a velocity
v << c or
interaction with the gas should significantly perturb the emission
line spectrum. However, because the filling factor in the emission
line region is small, it might be possible for a sufficiently
well-collimated relativistic beam to escape relatively unimpeded.
(c) To produce the observed superluminal motion, the motion must be
closely aligned with a narrow cone along the line of sight which has
an a priori probability of
(d) According to Equation (10) the flux density of the approaching
component should be very much greater than that of a receding or
stationary component by factors of ~ 106 and 103
respectively (for
Problems (a), (b), and (d) may be avoided if there is no actual
material moving with high velocity, but only an electromagnetic wave
that "ignites" stationary matter in the manner first discussed by
Rees (1971) and
Lynden-Bell (1977),
but problem (c) still remains in this case.
If, however, there is actual material moving, then the large
fraction of sources that show evidence for superluminal motion and the
apparent equality in the flux density of components might be explained
as a selection effect. Only those components that are moving towards
the observer and have enhanced emission due to the Doppler beaming are
observed. Two variations of this model may be considered: many
components may be ejected more or less isotropically, and owing to the
relatively poor dynamic range of the VLBI maps, only the approaching
components are strong enough to observe; or there may be a preferred
axis for each source, and only those sources with axes pointed towards
the observer are sufficiently strong to be observed.
The constant position angles which have been observed for the
multiple outbursts in 3C 120 and 3C 279 and the presence of
well-defined position angles which are found in many sources over a
wide range of dimensions make it difficult to accept the isotropic
models. In the models involving a preferred axis, symmetrically
ejected components, or pairs formed by the stationary nucleus and one
ejected component, are expected to suffer the effects of differential
Doppler beaming.
Scheuer & Readhead
(1979)
suggest that the appearance
of an expanding double may be due to a bright knot in the approaching
jet, seen together with radio emission from matter moving out from a
stationary nucleus, but the absence of the large expected flux
inequality is still contrived. It is also possible that the expanding
double is formed by two components ejected along the same track at
somewhat different velocities. The radiation from the slower component
is less sharply beamed, and
Cohen et al. (1979)
have shown that when
viewing at the appropriate angle an observer may see an appreciable
differential velocity from components with comparable flux densities.
Scheuer & Readhead
(1979)
have made the interesting suggestion that
the relativistic beaming models may account for those quasars that are
radio quiet, as they would then represent the large fraction of
objects with emission which is not beamed towards the observer within
a small angle
(a) More recent observations of bright optically selected quasars show
a much larger fraction of detections than previously found
(Condon et al. 1980,
D.B. Shaffer et al., unpublished,
Smith & Wright 1980).
Relativistic beaming cannot be important in the ~ 30 percent of the
optically bright that appear to be strong radio sources, because, with
the required broad beam, the relativistic enhancement is only about a
factor of 2.
(b) Some sources, such as 4C 39.25, show no evidence for relativistic
motion, yet have apparent luminosities comparable with the
superluminal sources. Thus, unless this is interpreted as a fortuitous
case of two components moving with the same velocity, or that
(c) High resolution observations of extended symmetric double radio
sources show that a large fraction contain bright compact components
that are coincident with the associated optical object
(Schilizzi 1976,
Preuss et al. 1977,
Owen et al. 1978,
Potash & Wardle 1979,
Gopal-Krishna et
al. 1980).
The extended doubles are expected to be
randomly oriented in space. Since, in those cases where data exist,
the compact components are aligned with the extended ones, they too
must be randomly oriented, and their apparent flux densities cannot be
significantly enhanced by Doppler beaming
(Kellermann 1978,
Readhead et al. 1978a,
Schilizzi et al. 1979,
Kellermann et al. 1981,
Linfield 1981,
Preuss et al. 1980).
(d) As discussed in the next section, optically selected quasars and
compact radio sources appear to have a very different spatial
distribution, so the Scheuer-Readhead interpretation would apparently
require that the probability of a favorable alignment, or the
distribution of y's, be a function of red shift.
(e) It is not clear how sources such as CTD 93, which are
well-separated doubles with nearly equal component fluxes and no
evidence of a jet, fit into this picture.
(f) 3C 273 is the brightest quasar in the sky at
optical, X-ray, and
Some of these problems, which were recognized by Scheuer & Readhead,
can be understood by appealing to more sophisticated models, for
example, with the value of
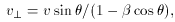
 is the angle between the
motion and the line of sight.
Figure 7a shows the observed velocity plotted
as a function of
is the angle between the
motion and the line of sight.
Figure 7a shows the observed velocity plotted
as a function of  for various
values of
for various
values of  . For
values of
. For
values of  ~ 90° the
effect of finite signal propagation time is unimportant and
v
~ 90° the
effect of finite signal propagation time is unimportant and
v ~ v, but for values of
~ v, but for values of  ~ 1/
~ 1/ ,
v
,
v can be very large. The maximum value of
v
can be very large. The maximum value of
v for a given value of
for a given value of  occurs when sin
occurs when sin  =
1/
=
1/ and is
vm =
and is
vm =
 v =
v =

 c. We note
also that, at
any given angle
c. We note
also that, at
any given angle  , there is
maximum velocity,
, there is
maximum velocity,
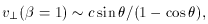

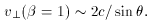
 is given by
is given by
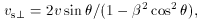
 =
1/
=
1/
 which is
vm =
which is
vm =
 c.
For values of
c.
For values of  ~ 1,
vm is nearly the same as for a single moving
object. This is because the receding component "barely moves" with an
apparent velocity ~ c/2.
~ 1,
vm is nearly the same as for a single moving
object. This is because the receding component "barely moves" with an
apparent velocity ~ c/2.
 ), that one
component of an oppositely directed
pair of ejected sources will be aligned to within an angle,
), that one
component of an oppositely directed
pair of ejected sources will be aligned to within an angle,
 , of the
line of sight is (1 - cos
, of the
line of sight is (1 - cos  )
(Figure 7b). For sin
)
(Figure 7b). For sin
 =
1/
=
1/ and for small
values of
and for small
values of  , (i.e.
, (i.e.
 >> 1),
P(
>> 1),
P( ) ~
1/2
) ~
1/2 2.
2.
 . The apparent
flux density of a moving component,
Sa(
. The apparent
flux density of a moving component,
Sa( ), in
terms of the flux density, S0, of the
same component at rest, is given by
(Ryle & Longair 1967)
), in
terms of the flux density, S0, of the
same component at rest, is given by
(Ryle & Longair 1967)
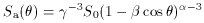
 , from the
direction of motion. The function
Sa(
, from the
direction of motion. The function
Sa( ) is shown
in Figure 7c for several values of
) is shown
in Figure 7c for several values of
 . When sin
. When sin
 =
1/
=
1/ (i.e.
v
(i.e.
v = vm), then (for
= vm), then (for
 = 0)
= 0)
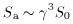
 >> 1, the apparent
flux density, Sa(0)
>> 1, the apparent
flux density, Sa(0)
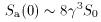
 ~ -1) is essentially invisible with
an apparent flux density, Sa(180), given by
~ -1) is essentially invisible with
an apparent flux density, Sa(180), given by
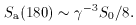
 0.99 c do introduce a
number of problems
(Jones & Burbidge 1973).
These are:
0.99 c do introduce a
number of problems
(Jones & Burbidge 1973).
These are:
 1 percent
(1/2
1 percent
(1/2 ); yet about
half of all
compact sources show evidence for superluminal motion, either from the
VLBI observations or, less directly, but for a much larger sample,
from the flux density variations.
); yet about
half of all
compact sources show evidence for superluminal motion, either from the
VLBI observations or, less directly, but for a much larger sample,
from the flux density variations.
 ~
5). This may be difficult to reconcile with the observations, which
typically show roughly comparable component flux densities, although,
as pointed out above, this may, at least in part, be an artifact of
the limited dynamic range. Moreover, relativistic time dilation
combined with a finite component lifetime could cause the exponent in
Equation (10) to be (2 -
~
5). This may be difficult to reconcile with the observations, which
typically show roughly comparable component flux densities, although,
as pointed out above, this may, at least in part, be an artifact of
the limited dynamic range. Moreover, relativistic time dilation
combined with a finite component lifetime could cause the exponent in
Equation (10) to be (2 -  )
rather than (3 -
)
rather than (3 -  ), and so reduce the
apparent discrepancy by an order of magnitude
(Scheuer & Readhead
1979).
), and so reduce the
apparent discrepancy by an order of magnitude
(Scheuer & Readhead
1979).
 ~
1/
~
1/ . In this model,
the radio emission from the
quasars is intrinsically weak, and the quasars have luminosities
comparable to the nuclei of nearby elliptical galaxies, but they
appear brightened by a factor ~ 103 (for
. In this model,
the radio emission from the
quasars is intrinsically weak, and the quasars have luminosities
comparable to the nuclei of nearby elliptical galaxies, but they
appear brightened by a factor ~ 103 (for
 ~ 7) as a result
of Doppler
beaming. Scheuer & Readhead also point out that the fraction of
quasars they expected to be observed as strong radio sources is ~
1/
~ 7) as a result
of Doppler
beaming. Scheuer & Readhead also point out that the fraction of
quasars they expected to be observed as strong radio sources is ~
1/ 2,
and furthermore that the number of quasars detected as radio
sources is expected to increase only very slowly with decreasing flux
density. Both of these predictions are qualitatively consistent with
the observations of radio quiet quasars
(Sramek & Weedman 1978,
Smith & Wright 1980,
Strittmatter et
al. 1980),
but there remain problems
with reconciling all of the observational material with the model, at
least in its simplest form.
2,
and furthermore that the number of quasars detected as radio
sources is expected to increase only very slowly with decreasing flux
density. Both of these predictions are qualitatively consistent with
the observations of radio quiet quasars
(Sramek & Weedman 1978,
Smith & Wright 1980,
Strittmatter et
al. 1980),
but there remain problems
with reconciling all of the observational material with the model, at
least in its simplest form.
 <<
1/
<<
1/ ,
the radiation must be isotropic and the intrinsic luminosity large.
,
the radiation must be isotropic and the intrinsic luminosity large.
 -ray wavelengths
and shows superluminal motion
(Pearson et al. 1981).
The a priori probability of finding an apparent value
-ray wavelengths
and shows superluminal motion
(Pearson et al. 1981).
The a priori probability of finding an apparent value
 ~ 10 is about
one percent. Since 3C 273 is unique on the basis of its bright optical
or X-ray emission alone, it is not possible to appeal to relativistic
beaming of the radio emission to explain this apparently fortuitous
coincidence. Doppler beaming of the nonthermal continuum does not
help, as the emission-line strength alone makes 3C 273 a unique
object, and there is no evidence that the emission-line region is
moving relativistically.
~ 10 is about
one percent. Since 3C 273 is unique on the basis of its bright optical
or X-ray emission alone, it is not possible to appeal to relativistic
beaming of the radio emission to explain this apparently fortuitous
coincidence. Doppler beaming of the nonthermal continuum does not
help, as the emission-line strength alone makes 3C 273 a unique
object, and there is no evidence that the emission-line region is
moving relativistically.
 correlated with
the presence of extended
emission, optical luminosity, and red shift, but then the model loses
much of its simplicity, and to these reviewers, its attractiveness.
correlated with
the presence of extended
emission, optical luminosity, and red shift, but then the model loses
much of its simplicity, and to these reviewers, its attractiveness.