

© CAMBRIDGE UNIVERSITY PRESS 1999
| |
1.3.2 Gravitational redshift
Einstein's general theory of relativity drew the attention of
astronomers to this source of redshift: indeed, the early
demonstrations of this effect were for the white dwarf stars Sirius B
and  Eridani B. In either case
the effect was very small, being less
than 0.001. Theoretically one could, on the basis of Schwarzschild's
solution, define the surface redshift of a mass M with radius
R by the formula
Eridani B. In either case
the effect was very small, being less
than 0.001. Theoretically one could, on the basis of Schwarzschild's
solution, define the surface redshift of a mass M with radius
R by the formula
Thus, by having R arbitrarily close to the critical value 2GM
/ c2, it
may seem possible to have large redshifts. This is not, however, the case.
In 1964 Hermann Bondi showed that whatever equation of state is
chosen, provided it is physically realistic (i.e., with sound speed in
the material not exceeding the speed of light), the surface redshift
cannot exceed 0.62. Thus surface gravitational redshift proved
inadequate to explain the large redshifts of quasars. There was also
an observational objection put forward by J. Greenstein and M. Schmidt
(1964). We briefly reproduce their elegant argument as applied to the
quasar 3C 273.
For small redshifts we get from the above formula
Consider a thin shell of radius R and thickness
Now suppose that the object is of stellar type with mass ~
M
Next we determine the volume of the shell and use the volume
emissivity of the H
where d is the expected distance of the source measured in
centimetres. This gives
Since the searches for proper motion of 3C 273 proved negative,
Greenstein and Schmidt assumed that the source could not be nearer
than 100 pc. This gave
This density is too high, and is precluded by the appearance of the
forbidden line [O III]
To get round this argument and the Bondi limit, Hoyle and Fowler
(1967) proposed a rather unusual model of a quasar in which the
redshift arose from light coming from the interior. In this model the
gravitational potential well at the centre of the object is provided
by a distribution of a large number of very compact objects (such as,
say, neutron stars). Any gas present in the system would descend to
the centre and settle down there and form the emission line region. It
is not difficult to see that the gravitating compact objects would
leave a sufficient gap for the central radiation to emerge with
redshifts much higher than the Bondi limit. The interior Schwarzschild
solution used by Hoyle and Fowler to demonstrate this effect gives
arbitrarily high central redshifts. However, more realistic models
discussed by P.K. Das (1977) yielded redshifts of the order of
2-3. These models also get around the Greenstein-Schmidt criticism
provided the masses are of galactic order.
We will take a second look at the gravitational redshift option in
Chapter 15, when considering other evidence that has a bearing on the
nature of redshifts.
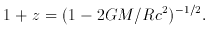
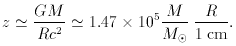
 R emitting radiation
in a line of width w. For line widths in 3C 273 arising from the
slight change of redshift over
R emitting radiation
in a line of width w. For line widths in 3C 273 arising from the
slight change of redshift over  R we get
R we get
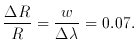
 . For
such an object a redshift 0.158 as in 3C 273 gives a radius of ~ 106
cm, and so
. For
such an object a redshift 0.158 as in 3C 273 gives a radius of ~ 106
cm, and so  R ~ 7 x
104 cm.
R ~ 7 x
104 cm.
 line to estimate the flux of radiation in that
line. For the source 3C 273 the volume emissivity at a temperature ~
104 K is ~ 10-25 ne2
erg sec-1 cm-3, where ne is the
electron number
density. Multiplying this with the volume of the shell and equating
the result to the observed luminosity we get
line to estimate the flux of radiation in that
line. For the source 3C 273 the volume emissivity at a temperature ~
104 K is ~ 10-25 ne2
erg sec-1 cm-3, where ne is the
electron number
density. Multiplying this with the volume of the shell and equating
the result to the observed luminosity we get
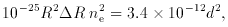
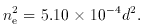
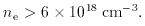
 5007
in the source spectrum. Thus the stellar
possibility is ruled out. Similarly Greenstein and Schmidt were able
to reject the alternative hypothesis that the source is much more
massive, extragalactic and located within, say, 25 Mpc.
5007
in the source spectrum. Thus the stellar
possibility is ruled out. Similarly Greenstein and Schmidt were able
to reject the alternative hypothesis that the source is much more
massive, extragalactic and located within, say, 25 Mpc.