Copyright © 1995 by Annual Reviews. All rights reserved
| Annu. Rev. Astron. Astrophys. 1995. 33:
581-624 Copyright © 1995 by Annual Reviews. All rights reserved |
Sections 4 and 5 review stellar- and gas-dynamical BH searches. Detections are listed in Table 1 (Section 2). Except for M33 (Section 4.8), we will not discuss MBH upper limits; these can be found in Bower et al. (1993) and in van den Bosch & van der Marel (1995).
This subject began with two papers on the stellar dynamics of M87
(Young et al. 1978; Sargent et al. 1978). They showed that
M87 contains an
MBH  3 x 109 M
3 x 109 M MDO if the stellar
velocity distribution is isotropic. We now know that isotropy is
unlikely, but these papers nevertheless
were seminal. Recently Harms et al. (1994) have confirmed the
Sargent and Young
conclusions using the refurbished HST. This work is based on
emission-line
spectroscopy, so we discuss it in Section 5.
MDO if the stellar
velocity distribution is isotropic. We now know that isotropy is
unlikely, but these papers nevertheless
were seminal. Recently Harms et al. (1994) have confirmed the
Sargent and Young
conclusions using the refurbished HST. This work is based on
emission-line
spectroscopy, so we discuss it in Section 5.
4.1 Search Technique
Dynamical mass measurements are conceptually simple. We need to deal with projection and atmospheric blurring (``seeing''); this is time-consuming, but it is routine. Mainly, the analysis is complicated because we need to be careful. This subject is dangerous. We enter it with expectations. We need to protect ourselves, lest we convince ourselves prematurely that we have proved what we expect to find.
The search technique is best described in the idealized case of spherical symmetry and a velocity ellipsoid that everywhere points at the center. Then the first velocity moment of the collisionless Boltzmann equation gives the mass M(r) within radius r,
where V is the rotation velocity;
All quantities in Equation 1 are unprojected. We observe projected
brightnesses, velocities, and velocity dispersions, so we must derive
the ranges of unprojected quantities that are consistent with the
observations after projection and seeing convolution. This is tricky.
Kormendy (1988a, c, d) and Dressler & Richstone (1988) independently
developed a method of deriving unprojected velocities from the data. Beginning
with a trial set of unprojected kinematics, they first calculate model spectra
projected along each line of sight by adding spectra of appropriate
V and
Some general properties of the mass measurements follow directly from
Equation 1. Rotation and random motions contribute similarly to
M(r), but the
Velocity anisotropy has usually been explored by constructing maximum
entropy dynamical models (Richstone & Tremaine 1984, 1988). Once anisotropy
becomes the default assumption, it is inherently difficult to prove that
an MDO
is required: the parameter space to be explored is large, and nature
knows more
distribution functions than we do. Therefore the biggest advantage of the
maximum entropy modeling technique is that it can easily be asked to find the
most extreme possible models in the most relevant directions in
parameter space.
In particular, it can be asked to minimize the central mass (it does so by
maximizing the anisotropy). If this fails - if M/L still rises
toward the
center - then we can be almost certain that an MDO is present.
We say ``almost'' because published maximum entropy models have had
significant limitations. Flattening corrections were made post hoc using
the tensor virial theorem. Also, the velocity dispersion
Progress in the BH search can come from improvements in analysis as well
as in observations. In particular, we can exploit LOSVDs. Their calculation
and use have been discussed, e.g., by Bender (1990); Rix & White (1992);
van der Marel & Franx (1993); Gerhard (1991, 1993a,b); Winsall & Freeman
(1993); Kuijken & Merrifield (1993); Dehnen & Gerhard (1993, 1994); Saha &
Williams (1994); Evans & de Zeeuw (1994); van der Marel et al.
(1994b); Bender
et al. (1994); and Statler (1995). It is convenient to measure
departures from
Gaussian LOSVDs using an expansion in Gauss-Hermite polynomials
Hi (van der
Marel & Franx 1993; Gerhard 1993a,b; Dehnen & Gerhard 1993):
where
M31 is the strongest BH case because of the rapid rotation and large
velocity dispersion in its nucleus (Dressler 1984; Kormendy 1987a, 1988a, c;
Dressler & Richstone 1988; Richstone et al. 1990). Its dynamics
have been
measured by four independent groups. And it is the first galaxy for which we
have made an iteration in improving the spatial resolution.
M31 contains the best known example of a nuclear star cluster (see
Johnson 1961; Kinman 1965; Sandage 1971 for reviews) that is dynamically
distinct from the bulge (Tremaine & Ostriker 1982). Light et al. (1974)
imaged it with Stratoscope II: at
The rapid rotation of the nucleus (discovered by Lallemand et al.
1960) and its steep central dispersion profile are shown in
Figure 5. Dressler &
Richstone (1988) and Kormendy (1988a,c) carried out analyses like those
described in the previous section. These were complementary: Kormendy
considered
uncertainties in the light distribution (particularly its flattening) in more
detail, and Dressler & Richstone showed that the results are independent of
velocity anisotropy. The mass-to-light ratio profiles are somewhat
model-dependent, but both papers showed that M/LV
rises near the center to values
The photometric asymmetry of the nucleus was known in 1988. Dressler,
Richstone, and Kormendy also observed asymmetries in the velocity field but
averaged over them in their analyses. The double nucleus complicates the BH
case. More detailed models should be constructed. However, it is
unlikely that M/LV is normal for an old stellar
population: the observed velocities would
have to overestimate the equilibrium virial velocities by a factor of
4. Instead, the HST observations are telling us something about the
formation of the nucleus.
Lauer et al. (1993) discuss possible explanations of the double nucleus;
none is very attractive. Extinction is unlikely: there is no color gradient.
M31 may have accreted and almost digested a compact elliptical like M32. But
timescales are a problem. At 2r = 0".49 = 1.7 pc (the projected
separation), a relative velocity of 200 km s-1 implies a
circular orbit period of 50,000y. Dynamical friction should result in a
merger within a few orbital times. Are we
just lucky to catch the nuclei in flagrante delicto? Two effects may
reduce the dynamical friction. If P1 is accreted, it may fortuitously
corotate with the stars of P2 (King et al. 1995). Alternatively,
both nuclei could be dominated
by BHs. This scenario is ad hoc but not implausible. We do not know whether
either effect is sufficient.
Finally, Tremaine (1995) has suggested a model in which the brightness
enhancement at P1 is caused by an eccentric nuclear disk. This model requires
that a 107.3-M
Bacon et al. (1994) add new information about the asymmetries by
presenting
two-dimensional V and
LOSVD observations by van der Marel et al. (1994a) are consistent
with this interpretation. They used the William Herschel Telescope (WHT; slit
width = 0".45,
More definite conclusions require higher spatial resolution. This is
expected from the new Subarcsecond Imaging Spectrograph (SIS) on the CFHT and
from HST. No absorption-line spectroscopy is available yet from
HST. However,
a second iteration of spectroscopy on BH candidate galaxies is under way by
Kormendy and collaborators using SIS.
SIS removes the main limitation of previous CFHT work: Herzberg Spectrograph
resolution was limited by camera optics to FWHM
Figure 7 shows SIS measurements of the M31
nucleus (Kormendy & Bender 1995). The LOSVD has two components. The
steep central rise in
The accretion hypothesis can be tested. King et al. (1995) make a
preliminary comparison of the stellar populations of P1 and P2 using a
HST will also be important for the BH case. Meanwhile, the dramatic
kinematics seen with SIS (Figure 7) support the
BH detection.
NGC 3115 is a edge-on S0 galaxy (Sandage 1961)
whose bulge provides 94% of the total light (Capaccioli et al. 1987).
At MB = -19.9, the bulge is almost as bright as a
giant elliptical, but it
rotates rapidly enough to be nearly isotropic (Illingworth & Schechter 1982).
Kormendy & Richstone (1992, hereafter KR92) showed that its steep central
kinematic gradients (Figure 8) make NGC 3115 the
strongest BH case after M31.
KR92 derived dynamical models that bracket the observations after projection
and seeing convolution. Figure 8 (left)
illustrates the best-fitting isotropic
model at three spatial resolutions. The
Finally, the top curves in each panel of
Figure 8 (left) show the best-fitting
isotropic model from KR92 at HST resolution (0".25 aperture and
the Faint Object Spectrograph). Kormendy et al. (1995a) observed
NGC 3115 with HST in 1994
December. They will combine the results with the SIS data and will construct
new dynamical models. It is reasonable to expect that these observations will
complete step 1 of the BH search for NGC 3115: i.e., they should tell us
definitively whether or not an MDO is present.
What caveats remain?
DUST ABSORPTION
NUCLEAR BARS
VELOCITY ANISOTROPY
LINE-OF-SIGHT VELOCITY DISTRIBUTIONS
M/L RATIOS
To summarize: in NGC 3115, as in M31, the detection of an MDO is probably
secure. But the arguments that we are detecting a BH are not rigorous.
The first galaxy with convincing evidence for an MDO was the dwarf
elliptical M32; it is now the most thoroughly studied BH candidate. Like
M31, it was long ago known to rotate rapidly near the center (Walker 1962).
Dressler (1984) and Tonry (1984, 1987) measured its rotation curve with
These results were strengthened by Dressler & Richstone (1988), who
obtained
Figure 10 illustrates the kinematics.
The conclusions of Tonry, Dressler, and Richstone have now been confirmed
by three independent groups. They provide a significant iteration in spatial
resolution over the discovery observations, and they strengthen the analysis by
fitting LOSVDs. Therefore M32, with M31 and NGC 3115, is among the
most secure BH candidates.
Carter & Jenkins (1993) observed M32 with the WHT, a 0".45 slit, and
Van der Marel et al. (1994a) present additional WHT observations,
including measurements of Gauss-Hermite coefficients. As in other rotating
galaxies, h3 and V have opposite signs;
h3
Van der Marel et al. (1994b) construct M32 models with two-integral
distribution functions f (E, Lz), where E is
total energy and Lz is the
axial component of angular momentum. Without MDOs, these models fit V
(r) and h3 (r) - h6
(r), but they fail to fit the central dispersion gradient. In
fact, they predict that
Qian et al. (1995) take the moment equation models one step further by
calculating their distribution functions using the contour integral method of
Hunter & Qian (1993). They can then derive the complete LOSVDs and not just
their skewness. For the MBH = 1.8 x 106
M
Dehnen (1995) has made further f (E, Lz) models
of the van der Marel et al. (1994a) observations using a slightly
different technique. He recovers
f (E, 0) from
Van der Marel et al. (1994b), Qian et al. (1995), and
Dehnen (1995) improve on earlier analyses in several important ways. The
models are properly flattened, they fit the non-Gaussian LOSVDs, and
they fit kinematic observations at a variety of slit positions, not just
along the major axis. The latter point
is important: as van der Marel et al. (1994b) point out, Tonry's
(1984, 1987)
models explain the major-axis dispersion gradient as due to rotational line
broadening, but without an intrinsic dispersion gradient, they cannot be in
dynamical equilibrium along the minor axis. The f (E,
Lz) models solve this problem.
These models also have an important shortcoming compared to the models
of Dressler & Richstone (1988). The distribution functions are
restricted to be functions
of two integrals; in many cases, they are required to be analytic. We can show
that these models fail to fit the data without a BH, but we cannot prove that
it is impossible to find a more general distribution function that succeeds
without a BH. In contrast, the maximum entropy models can be forced to
have the
smallest possible M/L as r -> 0. When this fails - subject to
shortcomings discussed in Section 4.1 - an MDO is
required. Thus the
distribution function and maximum entropy models are complementary: each has
strengths that the other lacks. It is reassuring that they agree. But an
exploration of extreme models that successfully fit V,
Finally, Figure 10 shows new observations of
M32 obtained with the CFHT and SIS (Kormendy et al. 1995a). These
provide a further improvement in spatial
resolution: The slit width was 0".35, and the seeing
In summary, five independent groups have observed and modeled M32.
Models without MDOs consistently fail to fit the kinematics. These include
maximum entropy models that were instructed to minimize the central
M/L. Successful models require that MBH
4.5 NGC 4594, The Sombrero Galaxy
(MBH
The remaining stellar-dynamical BH cases
(Sections 4.5, 4.6,
4.7) are weaker
than those of M31, M32, and NGC 3115 because the modeling analyses
have explored fewer degrees of freedom on M(r).
NGC 4594 is an almost edge-on Sa galaxy illustrated in the Hubble
Atlas (Sandage 1961). Its bulge is as luminous as a giant
elliptical (MB
Kormendy (1988d) observed NGC 4594 with the CFHT (slit width = 0".5, scale
= 0".435 pixel-1, seeing
The machinery of Section 4.1 was used to derive
unprojected rotation velocity,
velocity dispersion, and brightness profiles that bracket the bulge-subtracted
data after projection and seeing convolution. The solutions imply that the
mass-to-light ratio rises from normal values
M/LV
The main shortcoming of the analysis was that velocity anisotropy was not
explored. The rapid rotation and the nuclear disk make it unlikely that
The kinematics of NGC 4594 have been confirmed by five independent groups.
Jarvis & Dubath (1988) observed the galaxy with the ESO 3.6 m telescope, a
2" slit, 1".17 pixels, and seeing
Wagner et al. (1989: ESO 2.2 m telescope, 1".87 pixels, 2"
slit) were the first to examine LOSVDs. These clearly show a superposition of
rapidly rotating, cold and slowly rotating, hot components. The
cross-correlation peaks at the center and at ±3".6 agree well with those
illustrated in Kormendy (1994). Wagner et al. (1989) derive a
seeing-corrected mass of (3 ± 1.2) x 109
M
The kinematics are further confirmed by Carter & Jenkins (1993: WHT,
0".34 pixels, 0".55 slit, seeing
Van der Marel et al. (1994a) took additional spectra with a 1".25 slit,
0".6 pixels, and seeing
In summary, the kinematics of NGC 4594 are well confirmed. But none of
the published measurements improves on the discovery resolution.
Also, there has been little progress on modeling. Emsellem et al.
(1994a) model the Kormendy data using multi-Gaussian expansions of the PSF and
galaxy light distributions. Again, isotropic models do not fit the dispersion
profile unless there is an MDO of mass 5 x 108
M
More definitive results on NGC 4594 should be available soon. Emsellem
et al. (1994b) have obtained two-dimensional spectroscopy with
0".39 spatial sampling on the CFHT. Kormendy et al. (1995a) have
taken CFHT SIS spectra with
4.6 The Galaxy (MBH
The center of our Galaxy is enormously complicated and well studied.
Excellent reviews (Genzel & Townes 1987; Morris 1993; Genzel et
al. 1994) and conferences (Backer 1987; Morris 1989; Genzel & Harris
1994) discuss the physics in detail. Papers on a possible Galactic BH
include Lynden-Bell & Rees (1971); Rees (1987); Phinney (1989); and de
Zeeuw (1993). Here we summarize the AGN evidence and gas dynamics
briefly and then concentrate on the stellar-dynamical BH search.
The radio source Sgr A* (Genzel et al. 1994, Figure 2.2) is
assumed to be the Galactic center; this is not certain. Sgr A* is
spectacularly tiny. Lo et al. (1985) measure a radius of
Genzel & Townes (1987) and Genzel et al. (1994) review the dynamics of
neutral and ionized gas near the center. Velocities of 100-140 km
s-1 imply masses of several x 106
M
Because of optical extinction, stellar velocities are usually measured using
K-band CO band heads. From the first papers (Sellgren et
al. 1987; Rieke & Rieke 1988), masses of
106-107 M
The best dynamical analyses are by Kent (1992) and by Evans & de Zeeuw
(1994). Kent notes that the central K-band starlight is a flattened
power law,
Kinematic measurements of a number of kinds of stars confirm these results
(e.g., OH/IR stars: Lindqvist et al. 1992; He I stars: Krabbe & Genzel
1993, quoted in Genzel et al. 1994). The dynamical mass distribution is
compared to that derived from the infrared light distribution in
Figure 11. Gas and
stellar kinematics agree remarkably well. The conclusion that there is (1 to
3) x 106 M
Haller et al. (1995) have remeasured the kinematics with a 1".3 slit
placed at several positions near Sgr A*. From He I lines in hot stars and
CO band heads in cool stars, they find masses at r < 1 pc that
are somewhat lower than those reviewed by Genzel et al.
(1994). Haller and collaborators
raise the possibility that some of the dark matter near the center may be
extended in radius. Then MBH
Most recently, Krabbe et al. (1995) have obtained two-dimensional
K-band spectroscopy of the central 8" x 8" at FWHM
= 1" resolution. From 35 individual stellar velocities (mostly
based on emission lines), they derive
Nevertheless, the Galactic center BH case is fundamentally more uncertain
than those of the best candidates. The observations are sensitive to
discreteness and population effects. Absorption-line measurements are not
luminosity-weighted along the line of sight because the CO bands disappear in
the central 0.5 pc. It is hard to be confident that a particular kinematic
tracer is distributed in radius like the 2.2 µm light (which
is used to
determine d ln
If the Galaxy contains a BH, it is starving in a blizzard of food. This
could be embarrassing (Section 7).
NGC 3377 is a normal elliptical galaxy illustrated in the Hubble
Atlas. At MB = -18.8, it rotates rapidly enough
to be nearly isotropic.
Its core is tiny, so small radii have large luminosity weight in projection.
The axial ratio is 0.5; since no elliptical is much flatter, NGC 3377 must be
nearly edge-on. Finally, the distance is only 9.9 Mpc. Therefore NGC 3377 is
an excellent target for a BH search.
Kormendy et al. (1995b, see Kormendy 1992a) observed NGC 3377
with the CFHT and resolution
One BH upper limit deserves discussion. M33 is a bulgeless Sc
galaxy with a nucleus like a giant globular cluster. Kormendy &
McClure (1993)
observed it with the CFHT and a camera that uses a tip-tilt mirror to partly
correct seeing. At resolution
The central relaxation time, Tr  r2 r / G [-
(d ln
r2 r / G [-
(d ln  ) / (d ln
r)
- (d ln
) / (d ln
r)
- (d ln  r2) / (d ln r) -
(1 -
r2) / (d ln r) -
(1 -  2
2 /
/  r2) -
r2) -
 2
2 /
/  r2)],
r2)],
 r,
r, 
 , and
, and

 are the radial and
azimuthal components of the velocity dispersion; G is the
gravitational constant. The density
are the radial and
azimuthal components of the velocity dispersion; G is the
gravitational constant. The density  is not the
total mass density
is not the
total mass density  , it is the density of the tracer population whose
kinematics we measure. We never see
, it is the density of the tracer population whose
kinematics we measure. We never see  , because the stars that contribute
most of the light contribute almost none of the mass. In practice,
calculations are made assuming
, because the stars that contribute
most of the light contribute almost none of the mass. In practice,
calculations are made assuming  (r)
(r)  volume brightness,
i.e., we assume that M/L for the tracer population is independent
of radius. This can be (but usually is not) checked using measurements
of color or line strength gradients.
volume brightness,
i.e., we assume that M/L for the tracer population is independent
of radius. This can be (but usually is not) checked using measurements
of color or line strength gradients.
 weighted by
the local volume brightness. They then convolve the
two-dimensional array of projected spectra with the point-spread
function (PSF).
Finally, they ``observe'' the model with their velocity calculator and iterate
it until it agrees with the data. Further, Kormendy does not try to prove
uniqueness; rather, he constructs fits that bracket the observations in surface
brightness I (r) and in projected V (r) and
weighted by
the local volume brightness. They then convolve the
two-dimensional array of projected spectra with the point-spread
function (PSF).
Finally, they ``observe'' the model with their velocity calculator and iterate
it until it agrees with the data. Further, Kormendy does not try to prove
uniqueness; rather, he constructs fits that bracket the observations in surface
brightness I (r) and in projected V (r) and  (r). In particular, he
derives low-mass ``error bar'' models in which V and
(r). In particular, he
derives low-mass ``error bar'' models in which V and  are too
small near the center. The above procedure is required because of the
complicated response of any velocity calculator to population mixes and to
rotational line broadening. It guarantees that non-Gaussian line-of-sight
velocity distributions (LOSVDs) are measured in the same way in the
galaxies and
models. (It does not guarantee that the models have the same LOSVDs as the
galaxies; more about this shortly.) If the implied M/L rises
rapidly as r -> 0, then we have found an MDO.
are too
small near the center. The above procedure is required because of the
complicated response of any velocity calculator to population mixes and to
rotational line broadening. It guarantees that non-Gaussian line-of-sight
velocity distributions (LOSVDs) are measured in the same way in the
galaxies and
models. (It does not guarantee that the models have the same LOSVDs as the
galaxies; more about this shortly.) If the implied M/L rises
rapidly as r -> 0, then we have found an MDO.
 2 r / G term is multiplied by a factor
that involves uncertainties
and that can be less than 1. So rapid rotation is a more secure indicator of
large masses than are large velocity dispersions. Second, Equation 1 shows why
velocity anisotropy is so important, especially in nonrotating giant
ellipticals. HST shows that these have shallow power-law profiles
I
2 r / G term is multiplied by a factor
that involves uncertainties
and that can be less than 1. So rapid rotation is a more secure indicator of
large masses than are large velocity dispersions. Second, Equation 1 shows why
velocity anisotropy is so important, especially in nonrotating giant
ellipticals. HST shows that these have shallow power-law profiles
I  r-0.1±0.1 at r <<
rb (Lauer et al. 1992a; Crane et al. 1993b;
Stiavelli et al. 1993; Kormendy et al. 1994, Forbes 1994;
Forbes et al. 1994;
Ferrarese et al. 1994; Lauer et al. 1995). Then -d
ln
r-0.1±0.1 at r <<
rb (Lauer et al. 1992a; Crane et al. 1993b;
Stiavelli et al. 1993; Kormendy et al. 1994, Forbes 1994;
Forbes et al. 1994;
Ferrarese et al. 1994; Lauer et al. 1995). Then -d
ln  / d ln r
/ d ln r  +1. The second term cannot be larger than +1. But the third and fourth
terms are negative if
+1. The second term cannot be larger than +1. But the third and fourth
terms are negative if  r is larger than
r is larger than 
 and
and

 . They can be as small as -1
each, so they can largely cancel the
first two terms. This does not prove that anisotropic models are realistic.
But it illustrates why they have been so successful in explaining the
kinematics of giant ellipticals without BHs (e.g., M87:
Section 5.1). In
contrast, a BH case is more secure if the density gradient is steep, other
things being equal. This is one reason why low-luminosity ellipticals like M32
(Section 4.4) and NGC 3377
(Section 4.7) are better BH candidates
than giant ellipticals: no core is resolved, so -d ln
. They can be as small as -1
each, so they can largely cancel the
first two terms. This does not prove that anisotropic models are realistic.
But it illustrates why they have been so successful in explaining the
kinematics of giant ellipticals without BHs (e.g., M87:
Section 5.1). In
contrast, a BH case is more secure if the density gradient is steep, other
things being equal. This is one reason why low-luminosity ellipticals like M32
(Section 4.4) and NGC 3377
(Section 4.7) are better BH candidates
than giant ellipticals: no core is resolved, so -d ln  / d ln r
/ d ln r  +2 in Equation 1.
+2 in Equation 1.

 in the
rotation direction was not completely free:
in the
rotation direction was not completely free:  2
2 +
V2 =
+
V2 =  2
2 . This means, for example, that it was never possible
to make isotropic models that rotate. Both limitations will be
removed in future
papers. Like other analyses in astronomy, the above procedures provide results
at some level of approximation. Strong BH cases (especially M31 and
NGC 3115) are ones in which the derived M/L is higher than normal
by an amount that is substantially larger than the uncertainties.
. This means, for example, that it was never possible
to make isotropic models that rotate. Both limitations will be
removed in future
papers. Like other analyses in astronomy, the above procedures provide results
at some level of approximation. Strong BH cases (especially M31 and
NGC 3115) are ones in which the derived M/L is higher than normal
by an amount that is substantially larger than the uncertainties.
 / sqrt(2
/ sqrt(2

 2)] e(v
- V)2 / -2
2)] e(v
- V)2 / -2  2
{1 +
2
{1 +  ni=3 hi Hi
[(v - V) /
ni=3 hi Hi
[(v - V) /  ]},
]},
 is
the line strength. If h3 < 0, then the LOSVD has extra
power on
the systemic-velocity side of V. If h4 is
negative (positive), then the
LOSVD is more square (triangular) than a Gaussian. The
h4 coefficient
provides direct observational constraints on the velocity anisotropy:
tangentially anisotropic models generally have h4 < 0;
radially anisotropic
models generally have h4 > 0 (e.g., Gerhard 1991,
1993a,b; van der
Marel & Franx 1993; Dehnen & Gerhard 1993; van der Marel et al. 1994b).
Application of LOSVDs to the BH search has been pioneered independently by
R. van der Marel and by O. Gerhard and their collaborators. The following
sections discuss the added confidence provided by this second iteration in the
analysis.
is
the line strength. If h3 < 0, then the LOSVD has extra
power on
the systemic-velocity side of V. If h4 is
negative (positive), then the
LOSVD is more square (triangular) than a Gaussian. The
h4 coefficient
provides direct observational constraints on the velocity anisotropy:
tangentially anisotropic models generally have h4 < 0;
radially anisotropic
models generally have h4 > 0 (e.g., Gerhard 1991,
1993a,b; van der
Marel & Franx 1993; Dehnen & Gerhard 1993; van der Marel et al. 1994b).
Application of LOSVDs to the BH search has been pioneered independently by
R. van der Marel and by O. Gerhard and their collaborators. The following
sections discuss the added confidence provided by this second iteration in the
analysis.
 *
*  0".1, it is asymmetric;
its axial ratio is
0".1, it is asymmetric;
its axial ratio is  0.6,
and the brightest spot is near the NE end.
Lauer et al. (1993) and Crane et al. (1993b) observed it
with HST; Lauer and collaborators show that the nucleus is double
(Figure 4).
0.6,
and the brightest spot is near the NE end.
Lauer et al. (1993) and Crane et al. (1993b) observed it
with HST; Lauer and collaborators show that the nucleus is double
(Figure 4).
 100 (Figure 5). This implies
that M31 contains an MDO
of mass MBH
100 (Figure 5). This implies
that M31 contains an MDO
of mass MBH  3 x 107 M
3 x 107 M .
.
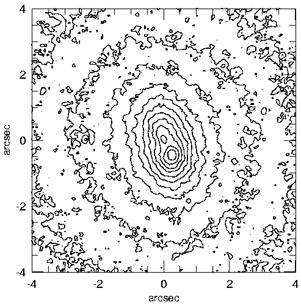
Figure 4. HST Planetary Camera V-band isophotes of
the nucleus and inner bulge of M31 after Lucy deconvolution (Lauer et
al. 1993).
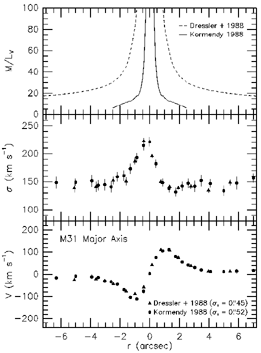
Figure 5. Rotation, dispersion, and M/L ratio profiles in
M31.
 BH dominate the potential, otherwise the lifetime of
P1 against differential precession is short. Accretion is one of several
possible ways that an eccentric nuclear disk could have formed. One advantage
of Tremaine's model is that it is specific enough to be testable with better
kinematic measurements.
BH dominate the potential, otherwise the lifetime of
P1 against differential precession is short. Accretion is one of several
possible ways that an eccentric nuclear disk could have formed. One advantage
of Tremaine's model is that it is specific enough to be testable with better
kinematic measurements.
 maps (Figure 6). They confirm the
conclusion
of Dressler & Richstone (1988) and of Kormendy (1988c) that the rotation curve
of the nucleus is symmetric about its center (``P2'' in Lauer et
al. 1993) and
not about the brightest point (``P1''). All studies also agree that the
center of the nucleus is the center of the bulge. But this is not the point of
maximum
maps (Figure 6). They confirm the
conclusion
of Dressler & Richstone (1988) and of Kormendy (1988c) that the rotation curve
of the nucleus is symmetric about its center (``P2'' in Lauer et
al. 1993) and
not about the brightest point (``P1''). All studies also agree that the
center of the nucleus is the center of the bulge. But this is not the point of
maximum  . Instead, the
brightest and hottest points are displaced from the
rotation center by similar amounts in opposite directions. Also,
. Instead, the
brightest and hottest points are displaced from the
rotation center by similar amounts in opposite directions. Also,  (r)
drops rapidly to or below the bulge dispersion on the brighter side of the
nucleus. It is natural to wonder (Lauer et al. 1993) whether P1 is cold.
Then the displacement of the
(r)
drops rapidly to or below the bulge dispersion on the brighter side of the
nucleus. It is natural to wonder (Lauer et al. 1993) whether P1 is cold.
Then the displacement of the  (r) peak from P2 could be due to a contribution from
P1 at the center.
(r) peak from P2 could be due to a contribution from
P1 at the center.
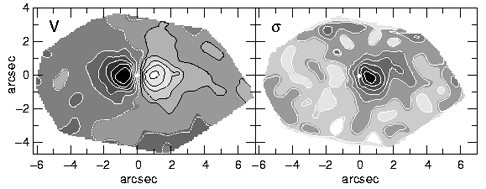
Figure 6. Contours of constant velocity (left) and
velocity dispersion (right) in the nucleus of M31 (Bacon et
al. 1994). The range of velocities (white to black) is
-120 km s-1  V
V  120 km s-1 and
140 km s-1
120 km s-1 and
140 km s-1 

 240 km s-1. These
CFHT observations have spatial sampling = 0".39 and resolution
240 km s-1. These
CFHT observations have spatial sampling = 0".39 and resolution  *
*  0".37. The major axis of the
nucleus is horizontal; the white dot marks its photometric center.
0".37. The major axis of the
nucleus is horizontal; the white dot marks its photometric center.
 * = 0".32). They show that the Gauss-Hermite
coefficient h3 (r) is opposite in sign to V
(r), with a strong negative peak,
h3
* = 0".32). They show that the Gauss-Hermite
coefficient h3 (r) is opposite in sign to V
(r), with a strong negative peak,
h3  -0.17, near P1. This suggests that the LOSVD consists of a hot
component that rotates slowly plus a cold one that rotates rapidly.
-0.17, near P1. This suggests that the LOSVD consists of a hot
component that rotates slowly plus a cold one that rotates rapidly.
 0".7. SIS optics are
better than the seeing. The scale is 0".0864 pixel-1; slit
widths of 0".3 can be used. Tip-tilt guiding is incorporated; by
offsetting the guide probe, the observer can center the object on the
slit to one-pixel accuracy. As
a result, the resolution is limited only by seeing and telescope aberrations.
Resolution FWHM
0".7. SIS optics are
better than the seeing. The scale is 0".0864 pixel-1; slit
widths of 0".3 can be used. Tip-tilt guiding is incorporated; by
offsetting the guide probe, the observer can center the object on the
slit to one-pixel accuracy. As
a result, the resolution is limited only by seeing and telescope aberrations.
Resolution FWHM  0".45 (
0".45 ( * = 0".19) is reasonably
common. Few objects are bright enough to be observed with HST at
< 0".25 resolution, so SIS remains interesting in the HST era.
* = 0".19) is reasonably
common. Few objects are bright enough to be observed with HST at
< 0".25 resolution, so SIS remains interesting in the HST era.
 seen
by previous authors is a feature of P2: P2 is much hotter than the bulge near
the center. But P1 is colder than the bulge at all radii. The LOSVDs
and the V and
seen
by previous authors is a feature of P2: P2 is much hotter than the bulge near
the center. But P1 is colder than the bulge at all radii. The LOSVDs
and the V and  fits
imply that P1 has
fits
imply that P1 has 
 85 km s-1 at
the center. This supports the idea that P1 is an accreted low-luminosity
stellar
system. Since P1 overlaps P2 at the center, it also confirms that the
85 km s-1 at
the center. This supports the idea that P1 is an accreted low-luminosity
stellar
system. Since P1 overlaps P2 at the center, it also confirms that the
 (r) asymmetry is due to
the contribution of P1 at P2.
(r) asymmetry is due to
the contribution of P1 at P2.

 175 nm image obtained with
HST. In the UV, P2 has a higher surface
brightness than P1. But the excess flux is small; it is equivalent to one
post-asymptotic-branch giant star.
King et al. (1995) suggest that it is due to the central radio
source (Table 1).
They also confirm that P1 is compact (its brightness drops to zero at
r
175 nm image obtained with
HST. In the UV, P2 has a higher surface
brightness than P1. But the excess flux is small; it is equivalent to one
post-asymptotic-branch giant star.
King et al. (1995) suggest that it is due to the central radio
source (Table 1).
They also confirm that P1 is compact (its brightness drops to zero at
r  0".63) and faint (V
0".63) and faint (V  14.8; MV
14.8; MV  -9.7). P1 is no brighter than
a large globular cluster, although it is much denser. Most interestingly, King
et al. (1995) see no sign that the (UV - optical) color of P1 is
different from
that of the bulge. This does not favor accretion. On the other hand, P1
nowhere contributes more than 55% of the total surface brightness. It is
difficult to measure its metallicity free of contamination from P2. It
will be important to see whether HST shows a drop in spectral line
strengths at P1.
-9.7). P1 is no brighter than
a large globular cluster, although it is much denser. Most interestingly, King
et al. (1995) see no sign that the (UV - optical) color of P1 is
different from
that of the bulge. This does not favor accretion. On the other hand, P1
nowhere contributes more than 55% of the total surface brightness. It is
difficult to measure its metallicity free of contamination from P2. It
will be important to see whether HST shows a drop in spectral line
strengths at P1.
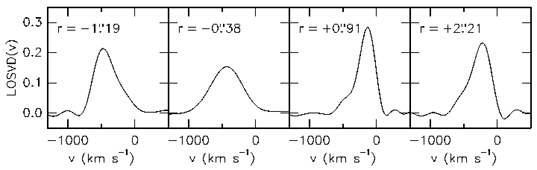
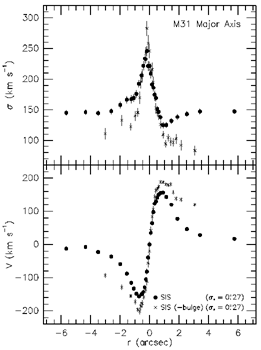
Figure 7. Line-of-sight velocity
distributions (top) and
V (r) and  (r)
profiles (bottom) along the nucleus major axis of M31 (Kormendy
& Bender 1995). Filled circles show the kinematics of the nucleus plus
bulge as observed; crosses show the nuclear kinematics after the bulge
spectrum is subtracted.
(r)
profiles (bottom) along the nucleus major axis of M31 (Kormendy
& Bender 1995). Filled circles show the kinematics of the nucleus plus
bulge as observed; crosses show the nuclear kinematics after the bulge
spectrum is subtracted.
 * = 0".44 lines are for the
resolution of the KR92 observations; by construction, they fit the open
circles. One iteration of improved spatial resolution is now
available. The filled circles in Figure 8 show
CFHT SIS measurements obtained with a 0".3 slit. At
* = 0".44 lines are for the
resolution of the KR92 observations; by construction, they fit the open
circles. One iteration of improved spatial resolution is now
available. The filled circles in Figure 8 show
CFHT SIS measurements obtained with a 0".3 slit. At
 * = 0".244 ±
0".015, V (r) already reaches its asymptotic value
at 1", and the apparent central velocity dispersion has risen
from 295 ± 9 km s-1 to 343 ± 19 km
s-1. This is almost exactly the increase
predicted by the KR92 models. The middle lines show the
best-fitting isotropic model at
* = 0".244 ±
0".015, V (r) already reaches its asymptotic value
at 1", and the apparent central velocity dispersion has risen
from 295 ± 9 km s-1 to 343 ± 19 km
s-1. This is almost exactly the increase
predicted by the KR92 models. The middle lines show the
best-fitting isotropic model at  * = 0".244. It fits the rotation
curve well, and it falls slightly below the dispersion profile at the center.
Also, the isotropic models continue to bracket the data at the
improved resolution (Figure 8,
right). These models imply that
M/LV rises toward the center to
values much larger than those of old stellar populations
(Figure 9). Note
that M/LV has already risen by a factor of 5 at 1"; contrary
to the claim of Rix (1993), this is not a marginal MDO detection. In fact, the
MDO dominates gravitationally to rBH = G
MBH /
* = 0".244. It fits the rotation
curve well, and it falls slightly below the dispersion profile at the center.
Also, the isotropic models continue to bracket the data at the
improved resolution (Figure 8,
right). These models imply that
M/LV rises toward the center to
values much larger than those of old stellar populations
(Figure 9). Note
that M/LV has already risen by a factor of 5 at 1"; contrary
to the claim of Rix (1993), this is not a marginal MDO detection. In fact, the
MDO dominates gravitationally to rBH = G
MBH /  2
2  1".8. We see that rBH >>
1".8. We see that rBH >>  *. If the
M/LV gradient is due to a central dark mass added to
stars with constant M/LV (r), then MBH
*. If the
M/LV gradient is due to a central dark mass added to
stars with constant M/LV (r), then MBH
 109
M
109
M . The MDO
mass can be reduced by allowing
. The MDO
mass can be reduced by allowing  r to be
larger than
r to be
larger than 
 and
and 
 near the center (Equation 1), but
KR92 showed that MBH must be
near the center (Equation 1), but
KR92 showed that MBH must be  108
M
108
M or the
models predict too little rotation at r
or the
models predict too little rotation at r  1" to 2". We
conclude that a significant iteration in spatial resolution confirms the BH
case. This increases our confidence in the MDO detection.
1" to 2". We
conclude that a significant iteration in spatial resolution confirms the BH
case. This increases our confidence in the MDO detection.
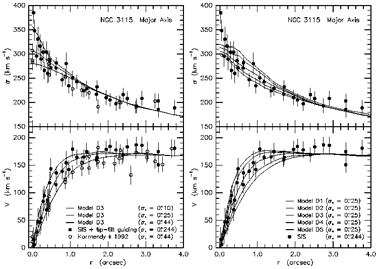
Figure 8. (Left) Kinematics of NGC 3115 compared with
the best-fitting isotropic model (D3) from KR92 as seen at various spatial
resolutions. (Right) SIS data compared with isotropic models D1 - D5
from KR92 as seen at  * = 0".25.
* = 0".25.
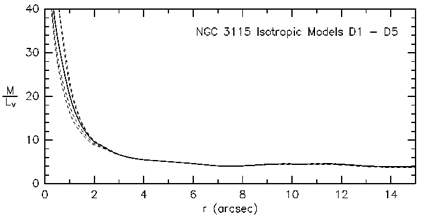
Figure 9. Mass-to-light ratio interior to radius r for the
isotropic models in Figure 8. All models have
M/LV  4 at
r
4 at
r  4" to 24"; this value
is normal for a bulge of MB = -19.9
(Kormendy 1987b, Figure 3). In
contrast, M/LV increases at r
< 2" by a factor of
4" to 24"; this value
is normal for a bulge of MB = -19.9
(Kormendy 1987b, Figure 3). In
contrast, M/LV increases at r
< 2" by a factor of  10. From KR92.
10. From KR92.
 2 r / G term would be
unaffected: Kormendy saw no dispersion anisotropy in NGC 936. (b) In
NGC 3115,
the end-on nuclear bar would have a true major-axis radius of
2 r / G term would be
unaffected: Kormendy saw no dispersion anisotropy in NGC 936. (b) In
NGC 3115,
the end-on nuclear bar would have a true major-axis radius of  4", since 1" (where
M/LV looks large) is
a pericenter radius. Such a bar would easily be seen in more face-on galaxies.
Some galaxies have nuclear bars (see Kormendy 1982 for a review). But we have
never seen one as elongated as the main bar in NGC 936, and argument
(a) suggests that even this is not enough. Nevertheless, nuclear
bar models should be investigated (Gerhard 1992).
4", since 1" (where
M/LV looks large) is
a pericenter radius. Such a bar would easily be seen in more face-on galaxies.
Some galaxies have nuclear bars (see Kormendy 1982 for a review). But we have
never seen one as elongated as the main bar in NGC 936, and argument
(a) suggests that even this is not enough. Nevertheless, nuclear
bar models should be investigated (Gerhard 1992).
 -0.05 at r
-0.05 at r  5". The above
authors emphasize that V (r) as derived by fitting a Gaussian to the
LOSVD then overestimates the true velocity moment in Equation 1. Van der
Marel et al. (1994a) worry that this accounts for the failure of
constant-M/L models to fit the kinematics. Similarly, the true
velocity dispersion is underestimated when
the LOSVD has large wings (van der Marel 1994a,b). Bender et al.
(1994; see their figure 3) provide the necessary corrections
5". The above
authors emphasize that V (r) as derived by fitting a Gaussian to the
LOSVD then overestimates the true velocity moment in Equation 1. Van der
Marel et al. (1994a) worry that this accounts for the failure of
constant-M/L models to fit the kinematics. Similarly, the true
velocity dispersion is underestimated when
the LOSVD has large wings (van der Marel 1994a,b). Bender et al.
(1994; see their figure 3) provide the necessary corrections  V and
V and 
 . At 0".5
. At 0".5  r
r  5" in NGC 3115,
5" in NGC 3115,
 V
V
 -14 to -21 km
s-1. The important point is that
-14 to -21 km
s-1. The important point is that  V is almost independent of radius. The corrected
rotation curve then reaches a slightly
lower asymptotic value at r
V is almost independent of radius. The corrected
rotation curve then reaches a slightly
lower asymptotic value at r  1"
to 5". However, model rotation curves are always scaled to the
asymptotic V; this is how the global M/L ratio is
derived. Thus the main result of the correction is to
lower the global (i.e.,bulge) M/LV. The change is only
~ 8%. It is small partly because less than half of M(r) as
derived from Equation 1 is due to V (r); the dispersion profile
is almost unchanged by the LOSVD correction. The strength of the BH
case is essentially unaffected, because the shape of the rotation curve
is almost unchanged. These remarks are reassuring. Nevertheless, as
van der Marel et al. (1994a) emphasize,
KR92 did not check whether the LOSVDs of their models fit those of the galaxy.
Models of NGC 3115 that exploit LOSVDs are planned (Kormendy et
al. 1995a).
1"
to 5". However, model rotation curves are always scaled to the
asymptotic V; this is how the global M/L ratio is
derived. Thus the main result of the correction is to
lower the global (i.e.,bulge) M/LV. The change is only
~ 8%. It is small partly because less than half of M(r) as
derived from Equation 1 is due to V (r); the dispersion profile
is almost unchanged by the LOSVD correction. The strength of the BH
case is essentially unaffected, because the shape of the rotation curve
is almost unchanged. These remarks are reassuring. Nevertheless, as
van der Marel et al. (1994a) emphasize,
KR92 did not check whether the LOSVDs of their models fit those of the galaxy.
Models of NGC 3115 that exploit LOSVDs are planned (Kormendy et
al. 1995a).
 1 to 10, with
M/LV
1 to 10, with
M/LV  L0.2 (Kormendy 1987a,b; Faber
et al. 1987; Djorgovski et al. 1988; Bender et al.
1992, 1993). The increase of
M/LV with L is due to three effects, the
metallicity-luminosity
correlation (Faber 1973; more luminous galaxies are more metal-rich, so stars
emit less V-band light per unit mass because of stronger
absorption-line blanketing), the anisotropy-luminosity correlation
(Davies et al. 1983), and an
age-luminosity correlation (Faber et al. 1992). Given that old stellar
populations contain stars with very large and very small mass-to-light ratios,
it is surprising that the scatter in M/L is so small. But the
small scatter is the reason why we interpret large nuclear M/L
ratios as implying MDOs.
Stellar densities in NGC 3115 are not outside the range observed in galaxies
that lack MDOs or in globular clusters. These have normal populations. The
spectra and colors of NGC 3115 also are normal. Therefore we have no reason to
expect a dramatic population gradient, and we see no evidence of one. An
extreme population gradient would be required: inside 1", the
dark star cluster would have to have about five times as much mass as the
visible stars. Therefore the most plausible conclusion is that NGC 3115
contains a central BH of mass MBH ~ 109
M
L0.2 (Kormendy 1987a,b; Faber
et al. 1987; Djorgovski et al. 1988; Bender et al.
1992, 1993). The increase of
M/LV with L is due to three effects, the
metallicity-luminosity
correlation (Faber 1973; more luminous galaxies are more metal-rich, so stars
emit less V-band light per unit mass because of stronger
absorption-line blanketing), the anisotropy-luminosity correlation
(Davies et al. 1983), and an
age-luminosity correlation (Faber et al. 1992). Given that old stellar
populations contain stars with very large and very small mass-to-light ratios,
it is surprising that the scatter in M/L is so small. But the
small scatter is the reason why we interpret large nuclear M/L
ratios as implying MDOs.
Stellar densities in NGC 3115 are not outside the range observed in galaxies
that lack MDOs or in globular clusters. These have normal populations. The
spectra and colors of NGC 3115 also are normal. Therefore we have no reason to
expect a dramatic population gradient, and we see no evidence of one. An
extreme population gradient would be required: inside 1", the
dark star cluster would have to have about five times as much mass as the
visible stars. Therefore the most plausible conclusion is that NGC 3115
contains a central BH of mass MBH ~ 109
M .
.
 *
*  0".5 to 0".85 seeing at the Hale
telescope; they demonstrated that the velocity dispersion rises
significantly toward the center.
Tonry (1984, 1987) fitted his data with isotropic dynamical models; these imply
that M/L increases toward the center. He concluded that M32
contains a BH of mass MBH
0".5 to 0".85 seeing at the Hale
telescope; they demonstrated that the velocity dispersion rises
significantly toward the center.
Tonry (1984, 1987) fitted his data with isotropic dynamical models; these imply
that M/L increases toward the center. He concluded that M32
contains a BH of mass MBH  (3 to 10) x 106
M
(3 to 10) x 106
M .
.
 *
*  0".5 observations of M32 with the Hale
telescope. Using the techniques of Section 4.1, they
showed that velocity anisotropy provides no escape from the conclusion
that an MDO is present. More detailed analysis by Richstone et
al. (1990) further supported the case.
0".5 observations of M32 with the Hale
telescope. Using the techniques of Section 4.1, they
showed that velocity anisotropy provides no escape from the conclusion
that an MDO is present. More detailed analysis by Richstone et
al. (1990) further supported the case.
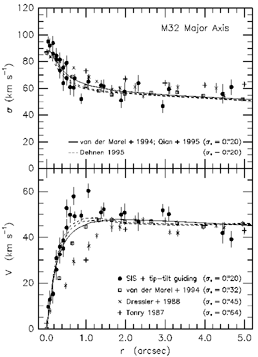
Figure 10. Kinematics of M32 compared with the dynamical
models of van der Marel et al. (1994b), Qian et al.
(1995), and Dehnen (1995) kindly recalculated by the above authors for
 * = 0".20.
* = 0".20.
 * = 0".34. At this
resolution, V (r) flattens out to 50 km s-1 at
~ 1". Carter & Jenkins do not use the dispersion profile
to measure masses, but they note that a high central M/L does not
follow from V (r) alone.
* = 0".34. At this
resolution, V (r) flattens out to 50 km s-1 at
~ 1". Carter & Jenkins do not use the dispersion profile
to measure masses, but they note that a high central M/L does not
follow from V (r) alone.
 -0.07 at
r
-0.07 at
r  1". Coefficients h4 - h6 are nearly
zero. Van der Marel and collaborators note that Tonry's (1987) isotropic
models do not fit h3 (r); in fact, they have
h3
1". Coefficients h4 - h6 are nearly
zero. Van der Marel and collaborators note that Tonry's (1987) isotropic
models do not fit h3 (r); in fact, they have
h3  0 at all
radii. This demonstrates an
interesting result: the LOSVDs are intrinsically asymmetric; they are not
Gaussians rendered asymmetric by rotational line broadening, projection, or
seeing. This is important for modelers who try to decipher the galaxy's
dynamics. But it does not have a large effect on the BH search, contrary to
worries expressed in van der Marel's paper. This can again be seen by
correcting
the Gaussian-fit rotation velocities to velocity moments appropriate for
Equation 1 using Bender et al. (1994). Since h3
0 at all
radii. This demonstrates an
interesting result: the LOSVDs are intrinsically asymmetric; they are not
Gaussians rendered asymmetric by rotational line broadening, projection, or
seeing. This is important for modelers who try to decipher the galaxy's
dynamics. But it does not have a large effect on the BH search, contrary to
worries expressed in van der Marel's paper. This can again be seen by
correcting
the Gaussian-fit rotation velocities to velocity moments appropriate for
Equation 1 using Bender et al. (1994). Since h3
 constant at r
constant at r
 1",
1",  V
V  -7 km s-1 is nearly independent
of radius (see also Figure 2 in Rix 1993). Thus, the main effect of the
correction is again to lower the bulge M/L. This is confirmed by
detailed analysis, as follows.
-7 km s-1 is nearly independent
of radius (see also Figure 2 in Rix 1993). Thus, the main effect of the
correction is again to lower the bulge M/L. This is confirmed by
detailed analysis, as follows.
 falls
toward the center at r <
1". [Physically: If stars cannot climb out of their own potential
well and therefore make a cuspy profile, they must be cold; see, e.g.,
Binney 1980; Dehnen 1993; Tremaine et al. 1994).] Similar results
are obtained with a moment equation analysis that fits V,
falls
toward the center at r <
1". [Physically: If stars cannot climb out of their own potential
well and therefore make a cuspy profile, they must be cold; see, e.g.,
Binney 1980; Dehnen 1993; Tremaine et al. 1994).] Similar results
are obtained with a moment equation analysis that fits V,  , and the skewness of the
LOSVDs. Good fits to
, and the skewness of the
LOSVDs. Good fits to  (r) are obtained when an MDO of mass MBH = (1.8
± 0.3) x 106 M
(r) are obtained when an MDO of mass MBH = (1.8
± 0.3) x 106 M is added. These results are in good agreement with
the conclusions of Tonry, Dressler, and Richstone.
is added. These results are in good agreement with
the conclusions of Tonry, Dressler, and Richstone.
 model, the
comparison to V,
model, the
comparison to V,  , and
h3 - h6 shows remarkably good
agreement along all slit positions measured by van der Marel et
al. (1994b).
, and
h3 - h6 shows remarkably good
agreement along all slit positions measured by van der Marel et
al. (1994b).
 using a Richardson (1972) - Lucy (1974) algorithm. The
distribution function is then multiplied by a guessed function of
Lz and used
to calculate V,
using a Richardson (1972) - Lucy (1974) algorithm. The
distribution function is then multiplied by a guessed function of
Lz and used
to calculate V,  , and
h3 - h6. These are compared to the
observations, and the distribution function is iterated until it agrees
with all
observables. Slit width, pixel size, and seeing are taken into account.
Dehnen's results are closely similar to those of van der Marel et
al. (1994b).
In particular, he confirms that such models do not fit the kinematics unless
they contain an MDO of mass MBH
, and
h3 - h6. These are compared to the
observations, and the distribution function is iterated until it agrees
with all
observables. Slit width, pixel size, and seeing are taken into account.
Dehnen's results are closely similar to those of van der Marel et
al. (1994b).
In particular, he confirms that such models do not fit the kinematics unless
they contain an MDO of mass MBH  (1.6 to 2) x 106
M
(1.6 to 2) x 106
M .
Again, the models with an MDO provide an excellent fit to
h3(r) - h6 (r)
along the major, minor, skew, and offset axes.
.
Again, the models with an MDO provide an excellent fit to
h3(r) - h6 (r)
along the major, minor, skew, and offset axes.
 , and hn
without the limitations of published maximum entropy models is still needed.
, and hn
without the limitations of published maximum entropy models is still needed.
 * was 0".20. At
this resolution, the central rotation curve is much steeper; it peaks at
V
* was 0".20. At
this resolution, the central rotation curve is much steeper; it peaks at
V  53 ± 2 km
s-1 at r
53 ± 2 km
s-1 at r  0".85. The central dispersion profile is
slightly steeper;
0".85. The central dispersion profile is
slightly steeper;  (0)
(0)  94 ± 2 km
s-1. Figure 10 compares
the SIS data with the models of van der Marel et al. (1994b),
Qian et al. (1995),
and Dehnen (1995) as seen at the present resolution. The fit is good at large
radii. But V (r) and
94 ± 2 km
s-1. Figure 10 compares
the SIS data with the models of van der Marel et al. (1994b),
Qian et al. (1995),
and Dehnen (1995) as seen at the present resolution. The fit is good at large
radii. But V (r) and  (r) both reach higher maximum values than the models
predict. Therefore the BH case gets stronger at SIS resolution. Modeling
of the SIS data is in progress.
(r) both reach higher maximum values than the models
predict. Therefore the BH case gets stronger at SIS resolution. Modeling
of the SIS data is in progress.
 2 x 106
M
2 x 106
M . This
result has survived improvements in spatial resolution of a factor of three
since the MDO discovery. Given expectations based on
Figure 10 and on the
predictions of Dehnen (1995) and Qian et al. (1995), HST
spectroscopy is feasible. Van der Marel et al. (1995) plan to
make these observations. Meanwhile, the case for an MDO is already strong.
. This
result has survived improvements in spatial resolution of a factor of three
since the MDO discovery. Given expectations based on
Figure 10 and on the
predictions of Dehnen (1995) and Qian et al. (1995), HST
spectroscopy is feasible. Van der Marel et al. (1995) plan to
make these observations. Meanwhile, the case for an MDO is already strong.
 5 x
108 M
5 x
108 M )
)
 -21.21 at 9.2 Mpc distance),
but it rotates rapidly enough so that
velocity anisotropies are small (Kormendy & Illingworth 1982). This reduces
the uncertainties in the mass measurements.
-21.21 at 9.2 Mpc distance),
but it rotates rapidly enough so that
velocity anisotropies are small (Kormendy & Illingworth 1982). This reduces
the uncertainties in the mass measurements.
 * = 0".40). The central kinematics
reveal a nuclear disk: at r
* = 0".40). The central kinematics
reveal a nuclear disk: at r  5" the rotation curve has an
inner peak, and the dispersion profile has a minimum (
5" the rotation curve has an
inner peak, and the dispersion profile has a minimum ( = 181 ± 6 km s-1)
that is significantly lower than the bulge dispersion (
= 181 ± 6 km s-1)
that is significantly lower than the bulge dispersion (
 240 km s-1). The nuclear disk is also detected
photometrically (Burkhead 1986, 1991;
Kormendy 1988d; Crane et al. 1993b; Emsellem et al.
1994a). Its presence guarantees that the LOSVDs are asymmetrical. But
the disk is well localized and significantly brighter than the bulge. At r
240 km s-1). The nuclear disk is also detected
photometrically (Burkhead 1986, 1991;
Kormendy 1988d; Crane et al. 1993b; Emsellem et al.
1994a). Its presence guarantees that the LOSVDs are asymmetrical. But
the disk is well localized and significantly brighter than the bulge. At r  10" to
15", both the photometry and the kinematics suggest that the
disk is negligible; here the major-axis dispersion is equal to that along the
minor axis. Therefore Kormendy subtracted the bulge spectrum obtained from the
minor axis and scaled to the major-axis bulge profile. He then confined his
analysis to the kinematics of the nuclear disk. This is a well-defined
kinematic subpopulation that can be used in Equation 1 to measure the
total mass distribution. Recently, Kormendy (1994) has shown that
asymmetries in the LOSVDs due to superposition of the nuclear disk and
bulge were removed by the decomposition; the Kormendy (1988d) models are
an adequate fit to the residual LOSVDs.
10" to
15", both the photometry and the kinematics suggest that the
disk is negligible; here the major-axis dispersion is equal to that along the
minor axis. Therefore Kormendy subtracted the bulge spectrum obtained from the
minor axis and scaled to the major-axis bulge profile. He then confined his
analysis to the kinematics of the nuclear disk. This is a well-defined
kinematic subpopulation that can be used in Equation 1 to measure the
total mass distribution. Recently, Kormendy (1994) has shown that
asymmetries in the LOSVDs due to superposition of the nuclear disk and
bulge were removed by the decomposition; the Kormendy (1988d) models are
an adequate fit to the residual LOSVDs.
 7.8 at large
radii to M/LV > 100 near the center. (All values in this
section have been corrected to the distance scale of
Table 1.) Kormendy & Westpfahl (1989)
showed that the outer M/LV remains constant to
~ 180". So a normal old stellar population dominates the bulge over a large
radius range. But an MDO is present at r < 1"; if
M/LV (r) = constant for the stellar population, then
MBH
7.8 at large
radii to M/LV > 100 near the center. (All values in this
section have been corrected to the distance scale of
Table 1.) Kormendy & Westpfahl (1989)
showed that the outer M/LV remains constant to
~ 180". So a normal old stellar population dominates the bulge over a large
radius range. But an MDO is present at r < 1"; if
M/LV (r) = constant for the stellar population, then
MBH  5 x
108 M
5 x
108 M .
.
 r >>
r >>  tangential (Kormendy &
Illingworth 1982; Jarvis & Freeman 1985). Nevertheless, anisotropic
models should be constructed.
tangential (Kormendy &
Illingworth 1982; Jarvis & Freeman 1985). Nevertheless, anisotropic
models should be constructed.
 *
*  0".51 to
0".64. Their data agree well with Kormendy's. They estimate the total mass
within 3".5 of the center to be 7 x 108 M
0".51 to
0".64. Their data agree well with Kormendy's. They estimate the total mass
within 3".5 of the center to be 7 x 108 M and ``conclude that there
is strong evidence that NGC 4594 contains a super-massive object, possibly a
black hole or massive star cluster.'' But they calculate no M/L
ratios, so they cannot tell how much of the mass is dark. In fact,
comparably luminous galaxies typically have core masses > 109
M
and ``conclude that there
is strong evidence that NGC 4594 contains a super-massive object, possibly a
black hole or massive star cluster.'' But they calculate no M/L
ratios, so they cannot tell how much of the mass is dark. In fact,
comparably luminous galaxies typically have core masses > 109
M in stars
(e.g., Kormendy 1982, Table 3). In NGC 4594, the luminosity inside 3".5
is LV
in stars
(e.g., Kormendy 1982, Table 3). In NGC 4594, the luminosity inside 3".5
is LV  6 x
108 L
6 x
108 L (Kormendy 1988d, Figure 10), and
M/LV,bulge
(Kormendy 1988d, Figure 10), and
M/LV,bulge  7.8. So Jarvis and Dubath underestimate the mass inside 3".5.
7.8. So Jarvis and Dubath underestimate the mass inside 3".5.
 inside 3".8
radius, but like Jarvis & Dubath (1988), they do not derive M/L ratios.
inside 3".8
radius, but like Jarvis & Dubath (1988), they do not derive M/L ratios.
 *
*  0".51). They remark that rotation alone is not rapid enough to imply a
large mass-to-light ratio. It is true that the central rise in
M/L found by Kormendy (1988d) is largely due to
the dispersion gradient. Checking anisotropy is probably more important than
Kormendy suggested.
0".51). They remark that rotation alone is not rapid enough to imply a
large mass-to-light ratio. It is true that the central rise in
M/L found by Kormendy (1988d) is largely due to
the dispersion gradient. Checking anisotropy is probably more important than
Kormendy suggested.
 * = 0".47. They agree with previous results.
The main new contribution is the measurement of LOSVDs. The maximum amplitude
of h3 = -0.15 is reached at r = 6";
|h3| - |h6| then
fall almost to zero at r = 10" - 20". This is
in excellent agreement with the Kormendy (1988d) and Burkhead (1991) conclusion
that the nuclear disk dominates near the center but is negligible at
intermediate radii.
* = 0".47. They agree with previous results.
The main new contribution is the measurement of LOSVDs. The maximum amplitude
of h3 = -0.15 is reached at r = 6";
|h3| - |h6| then
fall almost to zero at r = 10" - 20". This is
in excellent agreement with the Kormendy (1988d) and Burkhead (1991) conclusion
that the nuclear disk dominates near the center but is negligible at
intermediate radii.
 . However,
even the MDO model rotates too slowly. Part of the problem is that
Emsellem and collaborators fit the composite (not bulge-subtracted)
kinematics; this adds to the uncertainties because of the messy LOSVDs.
. However,
even the MDO model rotates too slowly. Part of the problem is that
Emsellem and collaborators fit the composite (not bulge-subtracted)
kinematics; this adds to the uncertainties because of the messy LOSVDs.
 * = 0".27; at this resolution, the apparent
central velocity dispersion is 282 ± 8 km s-1. They are
also scheduled to observe NGC 4594 with HST in 1995 February. The
issue of whether NGC 4594 contains an MDO should be settled soon.
* = 0".27; at this resolution, the apparent
central velocity dispersion is 282 ± 8 km s-1. They are
also scheduled to observe NGC 4594 with HST in 1995 February. The
issue of whether NGC 4594 contains an MDO should be settled soon.
 2 x 106
M
2 x 106
M )
)
 < (1.1 ± 0.1) x
10-3 arcsec = 9 AU at
< (1.1 ± 0.1) x
10-3 arcsec = 9 AU at  = 1.3 cm wavelength. Also,
= 1.3 cm wavelength. Also, 

 2 due
to interstellar electron scattering. Strong limits require short
2 due
to interstellar electron scattering. Strong limits require short
 ; at
3 mm,
; at
3 mm, 
 0.07 x 10-3 arcsec
= 0.6 AU (Rogers et al. 1994). This is only 15 times the
Schwarzschild radius of the 2 x 106
M
0.07 x 10-3 arcsec
= 0.6 AU (Rogers et al. 1994). This is only 15 times the
Schwarzschild radius of the 2 x 106
M MDO
suggested by the dynamics. It is easy to be impressed by the small
size. But as an AGN, Sgr A* is feeble: its radio luminosity is
1034 erg s-1 ~ 100.4 L
MDO
suggested by the dynamics. It is easy to be impressed by the small
size. But as an AGN, Sgr A* is feeble: its radio luminosity is
1034 erg s-1 ~ 100.4 L . The infrared and high-energy
luminosity is much higher (Genzel et al. 1994), but there is no
compelling need for a 106-M
. The infrared and high-energy
luminosity is much higher (Genzel et al. 1994), but there is no
compelling need for a 106-M BH. Mini-AGNs caused by
stellar-mass engines are known (e.g.,
Mirabel et al. 1992). So, to find out whether the Galaxy contains a
supermassive BH, we need dynamical evidence.
BH. Mini-AGNs caused by
stellar-mass engines are known (e.g.,
Mirabel et al. 1992). So, to find out whether the Galaxy contains a
supermassive BH, we need dynamical evidence.
 inside 1 pc
(Figure 11)
it if the gas is in circular motion. This assumption is not well
motivated: as discussed in Genzel et al. (1994), stellar winds
from luminous young stars
combine to make a wind blowing out of the central parsec; a few hundred
supernovae are thought to have occurred in the central 102 pc
in the past 104-105 y; some noncircular motions
are seen, including an expanding bubble of hot gas (Eckart et al.
1992). It is surprising that the motions are so close to
gravitational. Without confirmation from stellar dynamics, we would not
dare to include the Galaxy in Table 1.
inside 1 pc
(Figure 11)
it if the gas is in circular motion. This assumption is not well
motivated: as discussed in Genzel et al. (1994), stellar winds
from luminous young stars
combine to make a wind blowing out of the central parsec; a few hundred
supernovae are thought to have occurred in the central 102 pc
in the past 104-105 y; some noncircular motions
are seen, including an expanding bubble of hot gas (Eckart et al.
1992). It is surprising that the motions are so close to
gravitational. Without confirmation from stellar dynamics, we would not
dare to include the Galaxy in Table 1.
 at r
at r  1 pc were deduced. McGinn et al. (1989) and
Sellgren et al.(1990) measured spectra
of integrated starlight in apertures of 2".7 - 20" diameter.
The rotation curve rises in the inner 15" = 0.6 pc and then
flattens out at V
1 pc were deduced. McGinn et al. (1989) and
Sellgren et al.(1990) measured spectra
of integrated starlight in apertures of 2".7 - 20" diameter.
The rotation curve rises in the inner 15" = 0.6 pc and then
flattens out at V  36 km
s-1. The projected dispersion rises from ~
70 km s-1 at r > 35" to 125 km s-1 at
r < 20". Interestingly, the CO band strength decreases at small
radii; the true strength is consistent with zero at r < 15". The
authors suggest that the atmospheres of giant stars have been modified
(stripped off?) in the dense environment of the nucleus. This limits the
resolution to 0.6 pc, not much better than ground-based resolutions in
M31 and M32. Neglecting projection and anisotropy and assuming that
rc = 0.4 pc, McGinn et al. (1989)
conclude that the mass distribution is inconsistent with the light
distribution: it requires MBH
36 km
s-1. The projected dispersion rises from ~
70 km s-1 at r > 35" to 125 km s-1 at
r < 20". Interestingly, the CO band strength decreases at small
radii; the true strength is consistent with zero at r < 15". The
authors suggest that the atmospheres of giant stars have been modified
(stripped off?) in the dense environment of the nucleus. This limits the
resolution to 0.6 pc, not much better than ground-based resolutions in
M31 and M32. Neglecting projection and anisotropy and assuming that
rc = 0.4 pc, McGinn et al. (1989)
conclude that the mass distribution is inconsistent with the light
distribution: it requires MBH  2.5 x 106
M
2.5 x 106
M . Sellgren
et al. (1990) derive MBH
. Sellgren
et al. (1990) derive MBH  (5.5 ± 1.5) x 106
M
(5.5 ± 1.5) x 106
M .
.

 r-1.85. He
constructs a flattened, isotropic Jeans equation
model that fits the stellar and gas kinematics along the major and minor axes.
This requires an MDO of mass MBH
r-1.85. He
constructs a flattened, isotropic Jeans equation
model that fits the stellar and gas kinematics along the major and minor axes.
This requires an MDO of mass MBH  3 x 106
M
3 x 106
M . Evans & de
Zeeuw (1994) make f (E, Lz) models for the same
power-law density distribution; these fit the kinematics if
MBH
. Evans & de
Zeeuw (1994) make f (E, Lz) models for the same
power-law density distribution; these fit the kinematics if
MBH  2 x
106 M
2 x
106 M .
.
 of central dark matter even looks robust to the
poorly known core radius of the stars.
of central dark matter even looks robust to the
poorly known core radius of the stars.
 (1 to 2) x 106
M
(1 to 2) x 106
M .
.
 = 153 ± 18 km s-1 at < r >
= 0.245 pc and hence MBH
= 153 ± 18 km s-1 at < r >
= 0.245 pc and hence MBH  3 x 106
M
3 x 106
M . If the
velocity distribution is approximately isotropic, the case for a high central
mass-to-light ratio is quite strong.
. If the
velocity distribution is approximately isotropic, the case for a high central
mass-to-light ratio is quite strong.
 d ln
r and the stellar mass distribution). Given the
peculiar (young?, rejuvenated?) stellar population, it is not clear that
M/LK is constant for the stars. Also, no models have
explored anisotropy. On the other hand, we can hope for better spatial
resolution than in any other galaxy. The case for an massive dark object
is strong enough to be taken seriously. But further work is needed.
d ln
r and the stellar mass distribution). Given the
peculiar (young?, rejuvenated?) stellar population, it is not clear that
M/LK is constant for the stars. Also, no models have
explored anisotropy. On the other hand, we can hope for better spatial
resolution than in any other galaxy. The case for an massive dark object
is strong enough to be taken seriously. But further work is needed.
 8 x 107
M
8 x 107
M )
)
 *
*  0".48. The galaxy is kinematically similar to
M32: V (r) rises rapidly near the center to 100 km s-1
and then levels off;
0".48. The galaxy is kinematically similar to
M32: V (r) rises rapidly near the center to 100 km s-1
and then levels off;
 (r)
(r)  90 km s-1 at r
90 km s-1 at r
 2" and
then rises to 158 ± 11 km s-1 at the center. The
kinematics are confirmed by Bender et al. (1994). Kormendy et
al. (1995b) show that isotropic kinematic models
require an MDO of mass MBH
2" and
then rises to 158 ± 11 km s-1 at the center. The
kinematics are confirmed by Bender et al. (1994). Kormendy et
al. (1995b) show that isotropic kinematic models
require an MDO of mass MBH  8 x 107
M
8 x 107
M . They
also fail to find anisotropic models that fit without an MDO, but the failure
is not large. Therefore this is a weak MDO detection. After M32, NGC 3377
is only the second elliptical galaxy with stellar-dynamical evidence for
an MDO.
. They
also fail to find anisotropic models that fit without an MDO, but the failure
is not large. Therefore this is a weak MDO detection. After M32, NGC 3377
is only the second elliptical galaxy with stellar-dynamical evidence for
an MDO.
 * = 0".18, the limit on the core radius
is rc < 0.39 pc. This is as small as the smallest
cores in globular clusters. The central surface brightness is one of the
highest known (Figure 2). M33
is an excellent illustration of the fact that an unusually small and dense core
is no evidence for a BH unless kinematic measurements show high velocities
(Section 3). The central velocity
dispersion measured by Kormendy & McClure
(1993) is only 21 ± 3 km s-1. The central mass-to-light
ratio is M/LV
* = 0".18, the limit on the core radius
is rc < 0.39 pc. This is as small as the smallest
cores in globular clusters. The central surface brightness is one of the
highest known (Figure 2). M33
is an excellent illustration of the fact that an unusually small and dense core
is no evidence for a BH unless kinematic measurements show high velocities
(Section 3). The central velocity
dispersion measured by Kormendy & McClure
(1993) is only 21 ± 3 km s-1. The central mass-to-light
ratio is M/LV  0.4. Since this is required to explain the stellar
population, a conservative limit on MBH is the
limit on the core mass in stars: MBH
0.4. Since this is required to explain the stellar
population, a conservative limit on MBH is the
limit on the core mass in stars: MBH
 5 x 104
M
5 x 104
M . M33 is the
first giant galaxy in which a dead quasar engine can be ruled out.
. M33 is the
first giant galaxy in which a dead quasar engine can be ruled out.
 2 x 107 y, is so
short that core collapse has probably occurred. Also, the center is
2 x 107 y, is so
short that core collapse has probably occurred. Also, the center is
 (B - R) = 0.44 mag
bluer than the rest of the nucleus. The color gradient, the F-type
spectrum (van den Bergh 1991), and the small M/L ratio
imply that the nucleus contains young stars concentrated to the center.
Kormendy & McClure (1993) discuss the possibility that the stellar population
has been affected by dynamical processes (e.g., stellar collisions).
(B - R) = 0.44 mag
bluer than the rest of the nucleus. The color gradient, the F-type
spectrum (van den Bergh 1991), and the small M/L ratio
imply that the nucleus contains young stars concentrated to the center.
Kormendy & McClure (1993) discuss the possibility that the stellar population
has been affected by dynamical processes (e.g., stellar collisions).