


The cosmological interpretation of a measured microwave background power spectrum requires, to some extent, the introduction of a particular space of models. A very simple, broad, and well-motivated set of models are motivated by inflation: a universe described by a homogeneous and isotropic background with phase-coherent, power-law initial perturbations which evolve freely. This model space excludes, for example, perturbations caused by topological defects or other ``stiff'' sources, arbitrary initial power spectra, or any departures from the standard background cosmology. This set of models has the twin virtues of being relatively simple to calculate and best conforming to current power spectrum measurements. (In fact, most competing cosmological models, like those employing cosmic defects to make structure, are essentially ruled out by current microwave background and large-scale structure measurements.) This section will describe the parameters defining the model space and discuss the extent to which the parameters can be constrained through the microwave background.
The parameters defining the model space can be broken into three types: cosmological parameters describing the background space-time; parameters describing the initial conditions; and other parameters describing miscellaneous additional physical effects. Background cosmological parameters are:
 , the ratio of the total
energy density to the critical density
, the ratio of the total
energy density to the critical density
 c =
8
c =
8 / 3H2. This
parameter determines the spatial curvature of the universe:
/ 3H2. This
parameter determines the spatial curvature of the universe:
 = 1 is a flat universe with critical
density. Smaller values of
= 1 is a flat universe with critical
density. Smaller values of  correspond to a negative spatial
curvature, while larger values correspond to positive curvature.
Current microwave background measurements constrain
correspond to a negative spatial
curvature, while larger values correspond to positive curvature.
Current microwave background measurements constrain
 to be
roughly within the rage 0.8 to 1.2, consistent with a critical-density
universe.
to be
roughly within the rage 0.8 to 1.2, consistent with a critical-density
universe.
 b, the ratio of
the baryon density to the
critical density. Observations of the abundance of deuterium in high
redshift gas clouds and comparison with predictions from primordial
nucleosynthesis place strong constraints on this parameter
(Tytler et
al. 2000).
b, the ratio of
the baryon density to the
critical density. Observations of the abundance of deuterium in high
redshift gas clouds and comparison with predictions from primordial
nucleosynthesis place strong constraints on this parameter
(Tytler et
al. 2000).
 m, the ratio of
the dark matter density to the critical
density. Dynamical constraints, gravitational lensing, cluster
abundances, and numerous other lines of evidence all point to a total
matter density in the neighborhood of
m, the ratio of
the dark matter density to the critical
density. Dynamical constraints, gravitational lensing, cluster
abundances, and numerous other lines of evidence all point to a total
matter density in the neighborhood of
 0 =
0 =
 m +
m +
 b = 0.3.
b = 0.3.

 , the ratio of vacuum energy
density
, the ratio of vacuum energy
density
 to the critical
density. This is the notorious cosmological constant. Several years
ago, almost no cosmologist advocated a cosmological constant; now
almost every cosmologist accepts its existence. The shift was
precipitated by the Type Ia supernova Hubble diagram
(Perlmutter et
al. 1999,
Riess et al.
1998)
which shows an apparent acceleration in the
expansion of the universe. Combined with strong constraints on
to the critical
density. This is the notorious cosmological constant. Several years
ago, almost no cosmologist advocated a cosmological constant; now
almost every cosmologist accepts its existence. The shift was
precipitated by the Type Ia supernova Hubble diagram
(Perlmutter et
al. 1999,
Riess et al.
1998)
which shows an apparent acceleration in the
expansion of the universe. Combined with strong constraints on
 , a cosmological constant now
seems unavoidable, although
high-energy theorists have a difficult time accepting it. Strong
gravitational lensing of quasars places upper limits on
, a cosmological constant now
seems unavoidable, although
high-energy theorists have a difficult time accepting it. Strong
gravitational lensing of quasars places upper limits on

 (Falco et
al. 1998).
(Falco et
al. 1998).
Parameters describing the initial conditions are:
Other miscellaneous parameters include:
 . None of the current
neutrino oscillation results favor a cosmologically interesting
neutrino mass.
. None of the current
neutrino oscillation results favor a cosmologically interesting
neutrino mass.
 . This quantity
includes any particle species which is relativistic when it decouples
or can model entropy production prior to last scattering.
. This quantity
includes any particle species which is relativistic when it decouples
or can model entropy production prior to last scattering.
A realistic parameter analysis might include at least 8 free parameters. Given a particular microwave background measurement, deciding on a particular set of parameters and various priors on those parameters is as much art as science. For the correct model, parameter values should be insensitive to the size of the parameter space or the particular priors invoked. Several particular parameter space analyses are mentioned below in Sec. 6.5.
While the above parameters are useful and conventional for characterizing cosmological models, the features in the microwave background power spectrum depend on various physical quantities which can be expressed in terms of the parameters. Here the physical quantities are summarized, and their dependence on parameters given. This kind of analysis is important for understanding the model space of parameters as more than just a black box producing output power spectra. All of the physical dependences discussed here can be extracted from Hu and Sugiyama (1996). By comparing with numerical solutions to the evolution equations, Hu and Sugiyama demonstrated that they had accounted for all relevant physical processes.
Power-law initial conditions are determined in a straightforward way by the appropriate parameters Q, n, r, and nT, if the perturbations are purely adiabatic. Additional parameters must be used to specify any departure from power law spectra, or to specify an additional admixture of isocurvature initial conditions (e.g. Bucher et al. 1999). These parameters directly express physical quantities.
On the other hand, the physical parameters determining the evolution
of the initial perturbations until decoupling involve a few
specific combinations of cosmological parameters. First, note that the
density of radiation is fixed by the current microwave background
temperature which is known from COBE, as well as the density of the
neutrino backgrounds. The gravitational
potentials describing scalar perturbations determine the size of the
Sachs-Wolfe effect and also magnitude of the forces driving the acoustic
oscillations. The potentials are determined by
 0 h2, the
matter density as a fraction of critical density. The baryon density,
0 h2, the
matter density as a fraction of critical density. The baryon density,
 b
h2, determines the degree to which the acoustic peak
amplitudes are modulated as described above in
Sec. 5.4.
b
h2, determines the degree to which the acoustic peak
amplitudes are modulated as described above in
Sec. 5.4.
The time of matter-radiation equality is obviously determined solely by the
total matter density
 0
h2. This quantity affects the size of
the dark matter fluctuations, since dark matter starts to collapse
gravitationally only after matter-radiation equality. Also, the
gravitational potentials evolve in time during radiation domination
and not during matter domination: the later matter-radiation equality
occurs, the greater the time evolution of the potentials at
decoupling, increasing the Integrated Sachs-Wolfe effect.
The power spectrum also has a weak dependence on
0
h2. This quantity affects the size of
the dark matter fluctuations, since dark matter starts to collapse
gravitationally only after matter-radiation equality. Also, the
gravitational potentials evolve in time during radiation domination
and not during matter domination: the later matter-radiation equality
occurs, the greater the time evolution of the potentials at
decoupling, increasing the Integrated Sachs-Wolfe effect.
The power spectrum also has a weak dependence on
 0 in
models with
0 in
models with  0
significantly less than unity, because at late times the evolution of the
background cosmology will be dominated not by matter, but rather
by vacuum energy (for a flat universe with
0
significantly less than unity, because at late times the evolution of the
background cosmology will be dominated not by matter, but rather
by vacuum energy (for a flat universe with
 ) or by
curvature (for an open universe). In either case, the gravitational
potentials once again begin to evolve with time, giving an additional
late-time Integrated Sachs-Wolfe contribution, but this tends to affect
only the largest scales for which the constraints from measurements
are least restrictive due to cosmic variance (see the discussion
in Sec. 6.4 below).
) or by
curvature (for an open universe). In either case, the gravitational
potentials once again begin to evolve with time, giving an additional
late-time Integrated Sachs-Wolfe contribution, but this tends to affect
only the largest scales for which the constraints from measurements
are least restrictive due to cosmic variance (see the discussion
in Sec. 6.4 below).
The sound speed, which sets the sound horizon and thus affects
the wavelength of the acoustic modes (cf. Eq. (28)),
is completely determined by the baryon density
 b h2.
The horizon size at recombination, which sets the overall scale of the
acoustic oscillations, depends only on the total mass density
b h2.
The horizon size at recombination, which sets the overall scale of the
acoustic oscillations, depends only on the total mass density
 0
h2. The damping scale for diffusion damping depends
almost solely on the baryon density
0
h2. The damping scale for diffusion damping depends
almost solely on the baryon density
 b
h2, although numerical fits give a slight dependence on
b
h2, although numerical fits give a slight dependence on
 b alone
(Hu and Sugiyama
1996).
Finally, the angular diameter distance to the surface of last
scattering is determined by
b alone
(Hu and Sugiyama
1996).
Finally, the angular diameter distance to the surface of last
scattering is determined by
 0 h and
0 h and
 h; the angular
diameter sets the angular scale on the sky of the acoustic oscillations.
h; the angular
diameter sets the angular scale on the sky of the acoustic oscillations.
In summary, the physical dependence of the temperature perturbations
at last scattering depends on
 0
h2,
0
h2,
 b h2,
b h2,
 0 h, and
0 h, and
 h instead of the
individual cosmological
parameters
h instead of the
individual cosmological
parameters  0,
0,
 b, h, and
b, h, and
 . When analyzing
constraints on cosmological models from microwave background power
spectra, it may be more meaningful and powerful to constrain these
physical parameters rather than the cosmological ones.
. When analyzing
constraints on cosmological models from microwave background power
spectra, it may be more meaningful and powerful to constrain these
physical parameters rather than the cosmological ones.
6.3. Power spectrum degeneracies
As might be expected from the above discussion, not all of the
parameters considered here are independent. In fact, one nearly
exact degeneracy exists if
 0,
0,
 b, h, and
b, h, and
 are taken as independent parameters. To see this, consider a shift
in
are taken as independent parameters. To see this, consider a shift
in  0. In isolation,
such a shift will produce a corresponding
stretching of the power spectrum in l-space. But this effect can be
compensated by first shifting h to keep
0. In isolation,
such a shift will produce a corresponding
stretching of the power spectrum in l-space. But this effect can be
compensated by first shifting h to keep
 0
h2 constant,
then shifting
0
h2 constant,
then shifting  b to
keep
b to
keep  b
h2 constant, and finally
shifting
b
h2 constant, and finally
shifting  to keep the angular
diameter distance constant.
This set of shifted parameters will, in linear perturbation theory,
produce almost exactly the
same microwave background power spectra as the original set of parameters.
The universe with shifted parameters will generally not be flat, but
the resulting late-time Integrated Sachs-Wolfe effect only weakly
break the degeneracy. Likewise, gravitational lensing has only
a very weak effect on the degeneracy.
to keep the angular
diameter distance constant.
This set of shifted parameters will, in linear perturbation theory,
produce almost exactly the
same microwave background power spectra as the original set of parameters.
The universe with shifted parameters will generally not be flat, but
the resulting late-time Integrated Sachs-Wolfe effect only weakly
break the degeneracy. Likewise, gravitational lensing has only
a very weak effect on the degeneracy.
But all is not lost. The required shift in
 is
generally something like 8 times larger than the original shift
in
is
generally something like 8 times larger than the original shift
in  0, so although
the degeneracy is nearly exact,
most of the degenerate models represent rather extreme cosmologies.
Good taste requires either that
0, so although
the degeneracy is nearly exact,
most of the degenerate models represent rather extreme cosmologies.
Good taste requires either that
 = 0 or that
= 0 or that
 = 1, in
other words that we disfavor models which have both a cosmological
constant and are not flat. If such models are disallowed, the
degeneracy disappears. Finally, other observables not associated with
the microwave background break the degeneracy: the acceleration
parameter q0 =
= 1, in
other words that we disfavor models which have both a cosmological
constant and are not flat. If such models are disallowed, the
degeneracy disappears. Finally, other observables not associated with
the microwave background break the degeneracy: the acceleration
parameter q0 =
 0 / 2 -
0 / 2 -
 , for example,
is measured directly by the
high-redshift supernova experiments. So in practice, this
fundamental degeneracy in the microwave background power
spectrum between
, for example,
is measured directly by the
high-redshift supernova experiments. So in practice, this
fundamental degeneracy in the microwave background power
spectrum between  and
and
 is not likely to have
a great impact on our ability to constrain cosmological parameters.
is not likely to have
a great impact on our ability to constrain cosmological parameters.
Other approximate degeneracies in the temperature power spectrum exist between Q and r, and between zr and n. The first is illusory: the amplitudes of the scalar and tensor power spectra can be used in place of their sum and ratio, which eliminates the degeneracy. The power spectrum of large-scale structure will lift the latter degeneracy if bias is understood well enough, as will polarization measurements and small-scale second-order temperature fluctuations (the Ostriker-Vishniac effect, see Jaffe and Gnedin 2000) which are both sensitive to zr.
Finally, many claims have been made about the ability of the microwave
background to constrain the effective number of neutrino species or
neutrino masses. The effective number of massless degrees of freedom
at decoupling can be expressed in terms of the effective number of
neutrino species N (which does not need to be an integer). This
is a convenient way of parameterizing ignorance about fundamental
particle constituents of nature. Contributors to
N
(which does not need to be an integer). This
is a convenient way of parameterizing ignorance about fundamental
particle constituents of nature. Contributors to
N could
include, for example, an extra sterile neutrino sometimes invoked
in neutrino oscillation models, or the thermal background of gravitons
which would exist if inflation did not occur. This parameter can also
include the effects of entropy increases due to decaying or
annihilating particles; see Chapter 3 of
Kolb and Turner
(1990)
for a detailed discussion. As far as the microwave background is
concerned, N
could
include, for example, an extra sterile neutrino sometimes invoked
in neutrino oscillation models, or the thermal background of gravitons
which would exist if inflation did not occur. This parameter can also
include the effects of entropy increases due to decaying or
annihilating particles; see Chapter 3 of
Kolb and Turner
(1990)
for a detailed discussion. As far as the microwave background is
concerned, N determines the radiation energy density of the
universe and thus modifies the time of matter-radiation equality.
It can in principle be distinguished from a change
in
determines the radiation energy density of the
universe and thus modifies the time of matter-radiation equality.
It can in principle be distinguished from a change
in  0
h2 because it affects other physical parameters like
the baryon density or the angular diameter distance differently than
a shift in either
0
h2 because it affects other physical parameters like
the baryon density or the angular diameter distance differently than
a shift in either  0
or h.
0
or h.
Neutrino masses cannot provide
the bulk of the dark matter, because their free streaming greatly
suppresses fluctuation power on galaxy scales, leading to a drastic
mismatch with observed large-scale structure. But models with some
small fraction of dark matter as neutrinos have been advocated to
improve the agreement between the predicted and observed large-scale
structure power spectrum. Massive neutrinos have several small
effects on the microwave background, which have been studied
systematically by
Dodelson et
al. (1996).
They can slightly
increase the sound horizon at decoupling due to their transition from
relativistic to non-relativistic behavior as the universe expands.
More importantly, free streaming of massive neutrinos around the
time of last scattering leads to a faster decay of the gravitational
potentials, which in turn means more forcing of the acoustic
oscillations and a resulting increase in the monopole perturbations.
Finally, since matter-radiation equality is slightly delayed for
neutrinos with cosmologically interesting masses of a few eV, the
gravitational potentials are less constant
and a larger Integrated Sachs-Wolfe effect is induced. The change in
sound horizon and shift in matter-radiation equality due to
massive neutrinos cannot be
distinguished from changes in
 b
h2 and
b
h2 and
 0 h2, but
the alteration of the gravitational potential's time dependence due to
neutrino free streaming cannot be mimicked by some other change in
parameters. In principle the effect of neutrino masses can be
extracted from the microwave background, although the effects
are very small.
0 h2, but
the alteration of the gravitational potential's time dependence due to
neutrino free streaming cannot be mimicked by some other change in
parameters. In principle the effect of neutrino masses can be
extracted from the microwave background, although the effects
are very small.
Remarkably, the microwave background power spectrum contains enough information to constrain numerous parameters simultaneously (Jungman et al. 1996). We would like to estimate quantitatively just how well the space of parameters described above can be constrained by ideal measurements of the microwave background. The question has been studied in some detail; this section outlines the basic methods and results, and discusses how good various approximations are. For simplicity, only temperature fluctuations are considered in this section; the corresponding formalism for the polarization power spectra is developed in Kamionkowski et al. (1997).
Given a pixelized map of the microwave sky, we need to determine the
contribution of pixelization noise, detector noise, and beam width to
the multipole moments and power spectrum.
Consider a temperature map
of the sky
Tmap(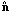 )
which is divided into
Npix equal-area pixels. The observed temperature in
pixel j is due to a cosmological signal plus noise,
Tmapj = Tj +
Tnoisej.
The multipole coefficients of the map can be constructed as
)
which is divided into
Npix equal-area pixels. The observed temperature in
pixel j is due to a cosmological signal plus noise,
Tmapj = Tj +
Tnoisej.
The multipole coefficients of the map can be constructed as
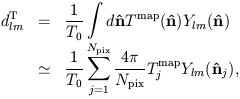
| (31) |
where 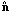 j is
the direction vector to pixel j.
The map moments are written as dlm to distinguish them from
the moments of the cosmological signal alm; the former
include the effects of noise. The extent to which the second line in
Eqs. (31) is only an approximate equality is
the pixelization noise. Most current experiments oversample the sky
with respect to their beam, so the pixelization noise is negligible.
Now assume
that the noise is uncorrelated between pixels and is well-represented
by a normal distribution. Also, assume that the map is created with
a gaussian beam with width
j is
the direction vector to pixel j.
The map moments are written as dlm to distinguish them from
the moments of the cosmological signal alm; the former
include the effects of noise. The extent to which the second line in
Eqs. (31) is only an approximate equality is
the pixelization noise. Most current experiments oversample the sky
with respect to their beam, so the pixelization noise is negligible.
Now assume
that the noise is uncorrelated between pixels and is well-represented
by a normal distribution. Also, assume that the map is created with
a gaussian beam with width
 b. Then it is
straightforward to show that the variance of the temperature moments is
given by
(Knox 1995)
b. Then it is
straightforward to show that the variance of the temperature moments is
given by
(Knox 1995)
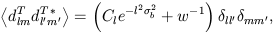
| (32) |
where  b =
0.00742(
b =
0.00742( b /
1°) and
b /
1°) and
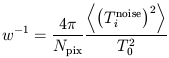
| (33) |
is the inverse statistical weight per unit solid angle, a measure of experimental sensitivity independent of the pixel size.
Now the power spectrum can be estimated via Eq. (32) as
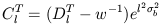
| (34) |
where
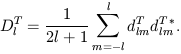
| (35) |
The individual coefficients dTlm are
gaussian random
variables. This means that ClT is a random
variable with a
 22l+1
distribution, and its variance is
(Knox 1995)
22l+1
distribution, and its variance is
(Knox 1995)
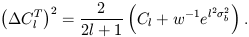
| (36) |
Note that even for w-1 = 0, corresponding to zero noise, the variance is non-zero. This is the cosmic variance, arising from the fact that we have only one sky to observe: the estimator in Eq. (35) is the sum of 2l + 1 random variables, so it has a fundamental fractional variance of (2l + 1)-1/2 simply due to Poisson statistics. This variance provides a benchmark for experiments: if the goal is to determine a power spectrum, it makes no sense to improve resolution or sensitivity beyond the level at which cosmic variance is the dominant source of error.
Equation (36) is extremely useful: it gives an estimate of how well the power spectrum can be determined by an experiment with a given beam size and detector noise. If only a portion of the sky is covered, the variance estimate should be divided by the fraction of the total sky covered. With these variances in hand, standard statistical techniques can be employed to estimate how well a given measurement can recover a given set s of cosmological parameters. Approximate the dependence of ClT on a given parameter as linear in the parameter; this will always be true for some sufficiently small range of parameter values. Then the parameter space curvature matrix (also known as the Fisher information matrix) is specified by
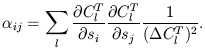
| (37) |
The variance in the determination of the parameter si from
a set of ClT with variances
 ClT after marginalizing
over all other parameters is given by the diagonal element i
of the matrix
ClT after marginalizing
over all other parameters is given by the diagonal element i
of the matrix  -1.
-1.
Estimates of this kind were first made by
Jungman et
al. (1996)
and subsequently refined by
Zaldarriaga et
al. (1997) and
Bond et al.
(1997),
among others. The basic result is that a map with pixels
of a few arcminutes in size and a signal-to-noise ratio of around 1
per pixel can determine  ,
,
 b h2,
b h2,
 m h2,
m h2,
 h2,
Q, n, and zr at the few percent
level simultaneously, up to the one degeneracy mentioned above
(see the table in
Bond et al.
1997).
Significant constraints will also be placed on r and
N
h2,
Q, n, and zr at the few percent
level simultaneously, up to the one degeneracy mentioned above
(see the table in
Bond et al.
1997).
Significant constraints will also be placed on r and
N . This prospect
has been the primary
reason that the microwave background has generated such excitement.
Note that
. This prospect
has been the primary
reason that the microwave background has generated such excitement.
Note that  , h,
, h,
 b, and
b, and
 are the classical
cosmological parameters. Decades of painstaking astronomical
observations have been devoted to determining the values of these
parameters. The microwave background offers a completely independent
method of determining them with comparable or significantly greater
accuracy, and with fewer astrophysical systematic effects to worry
about. The microwave background is also the only source of precise
information about the spectrum and character of the primordial
perturbations from which we arose. Of course, these exciting
possibilities hold only if the universe is accurately represented by a
model in the assumed model space. The model space is, however, quite
broad. Model-independent constraints which the microwave background
provides are discussed in Sec. 7.
are the classical
cosmological parameters. Decades of painstaking astronomical
observations have been devoted to determining the values of these
parameters. The microwave background offers a completely independent
method of determining them with comparable or significantly greater
accuracy, and with fewer astrophysical systematic effects to worry
about. The microwave background is also the only source of precise
information about the spectrum and character of the primordial
perturbations from which we arose. Of course, these exciting
possibilities hold only if the universe is accurately represented by a
model in the assumed model space. The model space is, however, quite
broad. Model-independent constraints which the microwave background
provides are discussed in Sec. 7.
The estimates of parameter variances based on the curvature matrix would be exact if the power spectrum always varied linearly with each parameter. This, of course, is not true in general. Given a set of power spectrum data, we want to know two pieces of information about the cosmological parameters: (1) What parameter values provide the best-fit model? (2) What are the error bars on these parameters, or more precisely, what is the region of parameter space which defines a given confidence level? The first question can be answered easily using standard methods of searching parameter space; generally such a search requires evaluating the power spectrum for fewer than 100 different models. This shows that the parameter space is generally without complicated structure or many false minima. The second question is more difficult. Anything beyond the curvature matrix analysis requires looking around in parameter space near the best-fit model. A specific Monte Carlo technique employing a Metropolis algorithm has recently been advocated (Christensen and Meyer 2000); such techniques will certainly prove more flexible and efficient than recent brute-force grid searches (Tegmark and Zaldarriaga 2000). As upcoming data sets contain more information and consequently have greater power to constrain parameters, efficient techniques of parameter space exploration will become increasingly important.
To this point, the discussion has assumed that the microwave background power spectrum is perfectly described by linear perturbation theory. Since the temperature fluctuations are so small, parts in a hundred thousand, linear theory is a very good approximation. However, on small scales, non-linear effects become important and can dominate over the linear contributions. The most important non-linear effects are the Ostriker-Vishniac effect coupling velocity and density perturbations (Jaffe and Kamionkowski 1998, Hu 2000), gravitational lensing by large-scale structure (Seljak 1996), the Sunyaev-Zeldovich effect which gives spectral distortions when the microwave background radiation passes through hot ionized regions (Birkinshaw 1999), and the kinetic Sunyaev-Zeldovich effect which doppler shifts radiation passing through plasma with bulk velocity (Gnedin and Jaffe 2000). All three effects are measurable and give important additional constraints on cosmology, but more detailed descriptions are outside the scope of these lectures.
Finally, no discussion of parameter determination would be complete without mention of galactic foreground sources of microwave emission. Dust radiates significantly at microwave frequencies, as do free-free and synchrotron emission; point source microwave emission is also a potential problem. Dust emission generally has a spectrum which rises with frequency, while free-free and synchrotron emission have falling frequency spectra. The emission is not uniform on the sky, but rather concentrated in the galactic plane, with fainter but pervasive diffuse emission in other parts of the sky. The dust and synchrotron/free-free emission spectra cross each other at a frequency of around 90 GHz. Fortunately for cosmologists, the amplitude of the foreground emission at this frequency is low enough to create a frequency window in which the cosmological temperature fluctuations dominate the foreground temperature fluctuations. At other frequencies, the foreground contribution can be effectively separated from the cosmological blackbody signal by measuring in several different frequencies and projecting out the portion of the signal with a flat frequency spectrum. The foreground situation for polarization is less clear, both in amplitude and spectral index, and could potentially be a serious systematic limit to the quality of cosmological polarization data. On the other hand, it may be no greater problem for polarization fluctuations than for temperature fluctuations. For an overview of issues surrounding foreground emission, see Bouchet and Gispert 1999 or the WOMBAT web site, http://astro.berkeley.edu/wombat.
6.5. Current constraints and upcoming experiments
As the Como School began, results from the high-resolution balloon-born experiment MAXIMA (Hanany et al. 2000) were released,complementing the week-old data from BOOMERanG (de Bernardis et al. 2000) and creating a considerable buzz at coffee breaks. The derived power spectrum estimates are shown in Fig. 3. The data from the two measurements appear consistent up to calibration uncertainties, and for simplicity will be referred to here as ``balloon data'' and discussed as a single result. While a few experimenters and data analyzers were members of both experimental teams, the measurements and data reductions were done essentially independently. Earlier data from the previous year (Miller et al. 1999) had clearly demonstrated the existence and angular scale of the first peak in the power spectrum and produced the first maps of the microwave background at angular scales below a degree. But the new results from balloon experiments utilizing extremely sensitive bolometric detecters represent a qualitative step forward. These experiments begin to exploit the potential of the microwave background for ``precision cosmology''; their power spectra put strong constraints on several cosmological parameters simultaneously and rule out many variants of cosmological models. In fact, what is most interesting is that, at face value, these measurements put significant pressure on all of the standard models outlined above.
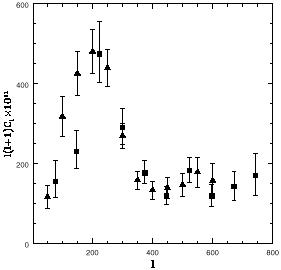
|
Figure 3. Two current measurements of the microwave background radiation temperature power spectrum. Triangles are BOOMERanG measurements multiplied by 1.21; squares are MAXIMA measurements multiplied by 0.92. The normalization factors are within the calibration uncertainties of the experiments, and were chosen by Hanany et al. (2000) to give the most consistent results between the two experiments. |
The balloon data shows two major features: first, a large peak in the
power spectrum centered around l = 200 with an amplitude of
approximately l2 Cl = 36000
µK2, and second, a broad plateau
between l = 400 and l = 700 with an amplitude of
approximately l2 Cl = 10000
µK2.
The first peak is clearly delineated and provides good
evidence that the universe is spatially flat, i.e.
 = 1.
The issue of a second acoustic peak is much less clear. In most flat
universe models with acoustic oscillations, the second peak is
expected to appear at an angular scale of around l = 400. The angular
resolution of the balloon experiments is certainly good enough to see
such a peak, but the power spectrum data shows no evidence for one. I
argue that a flat line is an excellent fit to the data past l = 300,
and that any model which shows a peak in this region will be a worse
fit than a flat line. This does not necessarily mean that no peak is
present; the error bars are too large to rule out a peak, but the
amplitude of such a peak is fairly strongly constrained to be lower
than expected given the first peak.
= 1.
The issue of a second acoustic peak is much less clear. In most flat
universe models with acoustic oscillations, the second peak is
expected to appear at an angular scale of around l = 400. The angular
resolution of the balloon experiments is certainly good enough to see
such a peak, but the power spectrum data shows no evidence for one. I
argue that a flat line is an excellent fit to the data past l = 300,
and that any model which shows a peak in this region will be a worse
fit than a flat line. This does not necessarily mean that no peak is
present; the error bars are too large to rule out a peak, but the
amplitude of such a peak is fairly strongly constrained to be lower
than expected given the first peak.
What does this mean for cosmological models? Within the model space outlined in the previous section, there are three ways to suppress the second peak. The first would be to have a power spectrum index n substantially less than 1. This solution would force abandonment of the assumption of power law initial fluctuations, in order to match the observed amplitude of large-scale structure at smaller scales. While this is certainly possible, it represents a drastic weakening in the predictive power of the microwave background: essentially, a certain feature is reproduced by arbitrarily changing the primordial power spectrum. While no physical principle requires power law primordial perturbations, we should wait for microwave background measurements on a much wider range of scales combined with overlapping large-scale structure measurements before resorting to departures from power-law initial conditions. If the universe really did possess an initial power spectrum with a variety of features in it, most of the promise of precision cosmology is lost. Recent power spectra extracted from the IRAS Point Source Survey Redshift Catalog (Tegmark and Hamilton 2000), which show a remarkable power law behavior spanning three orders of magnitude in wave number, seem to argue against this possibility.
The second possibility is a drastic amount of reionization. It is not clear the extent to which this might be compatible with the height of the first peak and still suppress the second peak sufficiently. This possibility seems unlikely as well, but would show clear signatures in the microwave background polarization.
The most commonly discussed possibility is that the very low second
peak amplitude reflects an unexpectedly large fraction of baryons
relative to dark matter in the universe. The baryon signature
discussed in Sec. 5.4
gives a suppression of the second peak in
this case.
However, primordial nucleosynthesis also constrains the
baryon-photon ratio. Recent high-precision measurements of deuterium
absorption in high-redshift neutral hydrogen clouds
(Tytler et
al. 2000)
give a baryon-photon number ratio of
 = 5.1 ± 0.5
× 1010, which translates to
= 5.1 ± 0.5
× 1010, which translates to
 b
h2 = 0.019 ± 0.002 assuming that the entropy
(i.e. photon
number) per comoving volume remains constant between nucleosynthesis
and the present.
Requiring
b
h2 = 0.019 ± 0.002 assuming that the entropy
(i.e. photon
number) per comoving volume remains constant between nucleosynthesis
and the present.
Requiring  b to
satisfy this nucleosynthesis
constraint leads to microwave background power spectra which are not
particularly good fits to the data. An alternative is that the entropy
per comoving volume has not remained fixed between
nucleosynthesis and recombination (see, e.g.,
Kaplinghat and
Turner 2000).
This could be arranged by having a
dark matter particle which decays to photons, although such a process
must evade limits from the lack of microwave background spectral
distortions
(Hu and Silk 1993).
Alternately, a
large chemical potential for the neutrino background could lead to
larger inferred values for the baryon-photon ratio from
nucleosynthesis
(Esposito et
al. 2000).
Either way, if both the microwave background
measurements and the high-redshift deuterium abundances hold up, the
discrepancy points to new physics.
Of course, a final explanation for the discrepancies is simply that
the balloon data has significant systematic errors.
b to
satisfy this nucleosynthesis
constraint leads to microwave background power spectra which are not
particularly good fits to the data. An alternative is that the entropy
per comoving volume has not remained fixed between
nucleosynthesis and recombination (see, e.g.,
Kaplinghat and
Turner 2000).
This could be arranged by having a
dark matter particle which decays to photons, although such a process
must evade limits from the lack of microwave background spectral
distortions
(Hu and Silk 1993).
Alternately, a
large chemical potential for the neutrino background could lead to
larger inferred values for the baryon-photon ratio from
nucleosynthesis
(Esposito et
al. 2000).
Either way, if both the microwave background
measurements and the high-redshift deuterium abundances hold up, the
discrepancy points to new physics.
Of course, a final explanation for the discrepancies is simply that
the balloon data has significant systematic errors.
I digress for a brief editorial comment about data analysis.
Straightforward searches of the conventional cosmological model space
described above for good fits to the balloon data give models with
very low dark matter densities, high baryon fractions, and very large
cosmological constants (see model P1 in Table 1 of
Lange et al.
2000).
Such models
violate other observational constraints on age, which must be at least
12 billion years (see, e.g.,
Peacock et
al. 1998),
and quasar and radio source strong
lensing number counts, which limit a cosmological constant to

 0.7
(Falco et
al. 1998).
The response to this situation so far has
been to invoke Bayesian prior probability distributions on various
quantities like
0.7
(Falco et
al. 1998).
The response to this situation so far has
been to invoke Bayesian prior probability distributions on various
quantities like  b
and the age. This leads to a best-fit model with a nominally acceptable
(Lange et
al. 2000,
Tegmark et
al. 2000
and others).
But be wary of this procedure when the priors
have a large effect on the best-fit model! The microwave background
will soon provide tighter constraints on most parameters than any
other source of prior information. Priors probabilities on a given
parameter are useful and justified when the microwave background data
has little power to constrain that parameter; in this case, the
statistical quality of the model fit to the microwave background data
will not be greatly affected by imposing the prior. However, something
fishy is probably going on when a prior pulls a parameter multiple
sigma away from its best fit value without the prior. This is what
happens presently with
b
and the age. This leads to a best-fit model with a nominally acceptable
(Lange et
al. 2000,
Tegmark et
al. 2000
and others).
But be wary of this procedure when the priors
have a large effect on the best-fit model! The microwave background
will soon provide tighter constraints on most parameters than any
other source of prior information. Priors probabilities on a given
parameter are useful and justified when the microwave background data
has little power to constrain that parameter; in this case, the
statistical quality of the model fit to the microwave background data
will not be greatly affected by imposing the prior. However, something
fishy is probably going on when a prior pulls a parameter multiple
sigma away from its best fit value without the prior. This is what
happens presently with
 b when the
nucleosynthesis prior is
enforced. If your priors make a big difference, it is likely either
that some of the data is incorrect, or that the model space does not
include the correct model. Both the microwave background measurements
and the high-redshift deuterium detections are taxing observations
dominated by systematic effects, so it is certainly possible that one
or both are wrong. On the other hand, MAXIMA and BOOMERanG are
consistent with each other while using different instruments,
different parts of the sky, and different analysis pipelines, and the
deuterium measurements are consistent for several different
clouds. This suggests possible missing physics ingredients, like
extreme reionization or an entropy increase mentioned above, or
perhaps significant contributions from
cosmic defects. It has even been suggested by
otherwise sober and reasonable people that the microwave background
results, combined with various difficulties related to dynamics of
spiral galaxies, may point towards a radical revision of the standard
cosmology
(Sellwood and
Kosowsky 2000).
We should not rest lightly
until the cosmological model preferred by microwave background
measurements is comfortably consistent with all relevant priors
derived from other data sources of comparable precision.
b when the
nucleosynthesis prior is
enforced. If your priors make a big difference, it is likely either
that some of the data is incorrect, or that the model space does not
include the correct model. Both the microwave background measurements
and the high-redshift deuterium detections are taxing observations
dominated by systematic effects, so it is certainly possible that one
or both are wrong. On the other hand, MAXIMA and BOOMERanG are
consistent with each other while using different instruments,
different parts of the sky, and different analysis pipelines, and the
deuterium measurements are consistent for several different
clouds. This suggests possible missing physics ingredients, like
extreme reionization or an entropy increase mentioned above, or
perhaps significant contributions from
cosmic defects. It has even been suggested by
otherwise sober and reasonable people that the microwave background
results, combined with various difficulties related to dynamics of
spiral galaxies, may point towards a radical revision of the standard
cosmology
(Sellwood and
Kosowsky 2000).
We should not rest lightly
until the cosmological model preferred by microwave background
measurements is comfortably consistent with all relevant priors
derived from other data sources of comparable precision.
The picture will come into sharper relief over the next two years. The MAP satellite (http://map.gsfc.nasa.gov), due for launch by NASA in May, 2001, will map the full microwave sky in five frequency channels with an angular resolution of around 15 arc minutes and a temperature sensitivity per pixel of a part in a million. Space missions offer unequalled sky coverage and control of systematics, and if it works as advertised, MAP will be a benchmark experiment. Prior to its launch, expect to see the first interferometric microwave data at angular scales smaller than a half degree from the CBI interferometer experiment (http://www.astro.caltech.edu/~tjp/CBI/). In this same time frame, we also may have the first detection of polarization. The most interesting power spectrum feature to focus on will be the existence and amplitude of a third acoustic peak. If a third peak appears with amplitude significantly higher than the putative second peak, this almost certainly indicates conventional acoustic oscillations with a high baryon fraction and possibly new physics to reconcile the result with the deuterium measurements. If, on the other hand, the power spectrum remains flat or falls further past the second peak region, then all bets are off. In a time frame of the next 5 to 10 years, we can reasonably expect to have a cosmic-variance limited temperature power spectrum down to scales of a few arcminutes (say, l = 4000), along with significant polarization information (though probably not cosmic-variance limited power spectra). In particular, ESA's Planck satellite mission (http://astro.estec.esa.nl/SA-general/Projects/Planck/) will map the microwave sky in nine frequency bands at significantly better resolution and sensitivity than the MAP mission. For a comprehensive listing of past and planned microwave background measurements, see Max Tegmark's experiments web page, http://www.hep.upenn.edu/~max/cmb/experiments.html.