


Having indirectly probed the nature of matter in the Universe using the previous estimates, it is now time to turn to direct constraints that have been derived in the past decade. Here, perhaps more than any other area of observational cosmology, new observations have changed the way we think about the Universe.
4.1. The Baryon Density: a re-occuring crisis?
The success of Big Bang Nucleosynthesis in predicting in the cosmic abundances of the light elements has been much heralded. Nevertheless, the finer the ability to empirically infer the primordial abundances on the basis of observations, the greater the ability to uncover some small deviation from the predictions. Over the past five years, two different sets of observations have threatened, at least in some people's minds, to overturn the simplest BBN model predictions. I believe it is fair to say that most people have accepted that the first threat was overblown. The concerns about the second have yet to fully subside.
i. Primordial Deuterium: The production of primordial deuterium during BBN is a monotonically decreasing function of the baryon density simply because the greater this density the more efficiently protons and neutrons get processed to helium, and deuterium, as an intermediary in this reactions set, is thus also more efficiently processed at the same time. The problem with inferring the primordial deuterium abundance by using present day measurements of deuterium abundances in the solar system, for example, is that deuterium is highly processed (i.e. destroyed) in stars, and no one has a good enough model for galactic chemical evolution to work backwards from the observed abundances in order to adequately constrain deuterium at a level where this constraint could significantly test BBN estimates.
Three years ago, the situation regarding deuterium as a probe of BBN changed dramatically, when David Tytler and Scott Burles convincingly measured the deuterium fraction in high redshift hydrogen clouds that absorb light from even higher redshift quasars. Because these clouds are at high redshift, before significant star formation has occurred, little post BBN deuterium processing is thought to have taken place, and thus the measured value gives a reasonable handle on the primordial BBN abundance. The best measured system [14] yields a deuterium to hydrogen fraction of
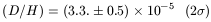
| (3) |
This, in turn, leads to a contraint on the baryon fraction of the Universe, via standard BBN,
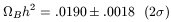
| (4) |
where the quoted uncertainty is dominated by the observational uncertainty in the D / H ratio, and where H0 = 100h. Thus, taken at face value, we now know the baryon density in the universe today to an accuracy of about 10%!
When first quoted, this result sent shock waves through some of the
BBN community, because this value of
 B is only consistent if the
primordial helium fraction (by mass) is greater than about 24.5%.
However, a number of previous studies had claimed an upper limit well
below this value. After the dust has settled, it is clear that
these previous claims are likely to under-estimated systematic
observational effects. Recent studies, for example, place an upper limit
on the primordial helium fraction closer to 25%.
B is only consistent if the
primordial helium fraction (by mass) is greater than about 24.5%.
However, a number of previous studies had claimed an upper limit well
below this value. After the dust has settled, it is clear that
these previous claims are likely to under-estimated systematic
observational effects. Recent studies, for example, place an upper limit
on the primordial helium fraction closer to 25%.
In any case, even if somehow the deuterium estimate is wrong, one can
combine all the other light element constraints to produce a range
for  b
h2 consistent with observation:
b
h2 consistent with observation:
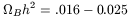
| (5) |
ii. CMB constraints: Beyond the great excitement over the observation of a peak in the CMB power spectrum at an angular scale corresponding to that expected for a flat universe lay some excitement/concern over the small apparent size of the next peak in the spectrum, at higher multipole moment (smaller angular size). The height of the first peak in the CMB spectrum is related to a number of cosmological parameters and thus cannot alone be used to constrain any one of them. However, the relative height of the first and second peaks is strongly dependent on the baryon fraction of the universe, since the peaks themselves arise from compton scattering of photons off of electrons in the process of becoming bound to baryons. Analyses of the two most recent small-scale CMB results produces a claimed constraint [9]:
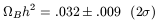
| (6) |
Depending upon how you look at this, this is either a stunning
confirmation that the overall scale for
 B predicted by simple
BBN analyses is correct, or a horrible crisis, in which the two
constraints, one from primordial deuterium, and one from CMB
observations, disagree at the two sigma level. Given the history of
this subject, I expect the former response is perhaps appropriate for the
moment. In particular, the CMB results are the very first to probe this
regime, and first observations are often suspect, and in addition, the
CMB peak heights do have a dependence on other cosmological parameters
which must be fixed in order to derive the above constraint on
B predicted by simple
BBN analyses is correct, or a horrible crisis, in which the two
constraints, one from primordial deuterium, and one from CMB
observations, disagree at the two sigma level. Given the history of
this subject, I expect the former response is perhaps appropriate for the
moment. In particular, the CMB results are the very first to probe this
regime, and first observations are often suspect, and in addition, the
CMB peak heights do have a dependence on other cosmological parameters
which must be fixed in order to derive the above constraint on
 B.
B.
Assuming the Burles and Tytler limit on
 B
h2 is correct, and
taking the range for H0 given earlier, one derives the
constraint on
B
h2 is correct, and
taking the range for H0 given earlier, one derives the
constraint on
 B of
B of
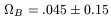
| (7) |
Perhaps the greatest change in cosmological prejudice in the past decade
relates to the inferred total abundance of matter in the Universe.
Because of the great intellectual attraction Inflation as a mechanism to
solve the so-called Horizon and Flatness problems in the Universe, it is
fair to say that most cosmologists, and essentially all particle
theorists had implicitly assumed that the Universe is flat, and thus that
the density of dark matter around galaxies and clusters of galaxies was
sufficient to yield  = 1. Over
the past decade it became more
and more difficult to defend this viewpoint against an increasing number
of observations that suggested this was not, in fact, the case in the
Universe in which we live.
= 1. Over
the past decade it became more
and more difficult to defend this viewpoint against an increasing number
of observations that suggested this was not, in fact, the case in the
Universe in which we live.
The earliest holes in this picture arose from measurements of galaxy clustering on large scales. The transition from a radiation to matter dominated universe at early times is dependent, of course, on the total abundance of matter. This transition produces a characteristic signature in the spectrum of remnant density fluctuations observed on large scales. Making the assumption that dark matter dominates on large scales, and moreover that the dark matter is cold (i.e. became non-relativistic when the temperature of the Universe was less than about a keV), fits to the two point correlation function of galaxies on large scales yielded [15, 16]:
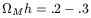
| (8) |
Unless h was absurdly small, this would imply that
 M is
substantially less than 1.
M is
substantially less than 1.
The second nail in the coffin arose when observations of the evolution
of large scale structure as a function of redshift began to be made.
Bahcall and collaborators
[17]
argued strongly that evidence for
any large clusters at high redshift would argue strongly against a flat
cold dark matter dominated universe, because in such a universe structure
continues to evolve with redshift up to the present time on large scales,
so that in order to be consistent with the observed structures at low
redshift, far less structure should be observed at high redshift. Claims
were made that an upper limit
 B
B
 0.5 could be obtained by
such analyses.
0.5 could be obtained by
such analyses.
A number of authors have questioned the systematics inherent in the early
claims, but it is certainly clear that there appears to be more structure
at high redshift than one would naively expect in a flat matter dominated
universe. Future studies of X-ray clusters, and use of the
Sunyaev-Zeldovich effect to measure cluster properties should be able to
yield measurements which will allow a fine-scale distinction not just
between models with different overall dark matter densities, but also
models with the same overall value of
 and different equations
of state for the dominant energy
[18].
and different equations
of state for the dominant energy
[18].
For the moment, however, perhaps the best overall constraint on the total density of clustered matter in the universe comes from the combination of X-Ray measurements of clusters with large hydrodynamic simulations. The idea is straightforward. A measurement of both the temperature and luminosity of the X-Rays coming from hot gas which dominates the total baryon fraction in clusters can be inverted, under the assumption of hydrostatic equilibrium of the gas in clusters, to obtain the underlying gravitational potential of these systems. In particular the ratio of baryon to total mass of these systems can be derived. Employing the constraint on the total baryon density of the Universe coming from BBN, and assuming that galaxy clusters provide a good mean estimate of the total clustered mass in the Universe, one can then arrive at an allowed range for the total mass density in the Universe [19, 20, 21]. Many of the initial systematic uncertainties in this analysis having to do with cluster modelling have now been dealt with by better observations, and better simulations ( i.e. see [22]), so that now a combination of BBN and cluster measurements yields:
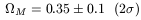
| (9) |
4.3. Equation of State of Dominant Energy
Remarkably, the above estimate for
 M brings the
discussion of cosmological parameters full circle, with consistency
obtained for a flat 12.5 billion year old universe , but not one dominated
by matter. As noted previously, a cosmological constant dominated
universe with
M brings the
discussion of cosmological parameters full circle, with consistency
obtained for a flat 12.5 billion year old universe , but not one dominated
by matter. As noted previously, a cosmological constant dominated
universe with
 M = 0.35 has an age
which nicely fits in the
best-fit range. However, based on the data discussed thus far, we have
no direct evidence that the dark energy necessary to result in a flat
universe actually has the equation of state appropriate for a vacuum
energy. Direct motivation for the possibility that the dominant energy
driving the expansion of the Universe violates the Strong Energy
Condition came, in 1998, from two different sets of observations of
distant Type 1a Supernovae. In measuring the distance-redshift relation
[23,
24]
these groups both came to the same, surprising
conclusion: the expansion of the Universe seems to be accelerating!
This is only possible if the dominant energy is
"cosmological-constant-like", namely if
M = 0.35 has an age
which nicely fits in the
best-fit range. However, based on the data discussed thus far, we have
no direct evidence that the dark energy necessary to result in a flat
universe actually has the equation of state appropriate for a vacuum
energy. Direct motivation for the possibility that the dominant energy
driving the expansion of the Universe violates the Strong Energy
Condition came, in 1998, from two different sets of observations of
distant Type 1a Supernovae. In measuring the distance-redshift relation
[23,
24]
these groups both came to the same, surprising
conclusion: the expansion of the Universe seems to be accelerating!
This is only possible if the dominant energy is
"cosmological-constant-like", namely if
 < - 0.5 (recall that
< - 0.5 (recall that
 = - 1 for a cosmological constant).
= - 1 for a cosmological constant).
In order to try and determine if the dominant dark energy does in fact
differ significantly from a static vacuum energy - as for example may
occur if some background field that is dynamically evolving is
dominating the expansion energy at the moment - one can hope to search for
deviations from the distance-redshift relation for a cosmological
constant-dominated universe. To date, none have been observed. In
fact, existing measurements already put an upper limit

 - 0.6
[25].
Recent work
[7]
suggests that the best one
might be able to do from the ground using SN measurements would be to
improve this limit to
- 0.6
[25].
Recent work
[7]
suggests that the best one
might be able to do from the ground using SN measurements would be to
improve this limit to

 - 0.7. Either other measurements,
such as galaxy cluster evolution observations, or space-based SN
observations would be required to further tighten the constraint.
- 0.7. Either other measurements,
such as galaxy cluster evolution observations, or space-based SN
observations would be required to further tighten the constraint.