It is important to remind ourselves of the definition of LINERs. Although
rigorous boundaries have little physical meaning and are, to some extent,
arbitrary, classification is operationally necessary.
Heckman (1980b)
originally defined LINERs strictly using the optical forbidden lines of
oxygen: [O II] 
3727 >
[O III] 5007 and [O I]
6300 > 0.33
[O III] 5007. Compared with
the spectra of Seyfert nuclei or H II
regions, the low-ionization states of oxygen in the spectra of LINERs are
unusually strong relative to its high-ionization states. Recognizing the
arbitrariness of this definition, Heckman drew attention to a group of
``transition objects'' whose spectra were intermediate between those of
``pure'' LINERs (as defined above) and classical Seyfert nuclei.
As a consequence of the near coincidence between the ionization potentials of
hydrogen and neutral oxygen, the collisionally-excited [O I] line in an
ionization-bounded nebula arises predominantly from the ``partially-ionized
zone,'' wherein both neutral oxygen and free electrons coexist. In addition
to O0, the conditions of the partially-ionized zone are also
favorable for
S+ and N+, whose ionization potentials are 23.3 eV
and 29.6 eV,
respectively. Hence, in the absence of abundance anomalies, [N II]
6548, 6583 and [S II]
6716, 6731 are strong (relative to, say,
H
) whenever [O I]
6300, 6363 are strong, and vice versa. This
theoretical expectation and the empirical evidence that extragalactic H II
regions rarely exhibit [N II]
6583 / H
0.6 (e.g.,
Searle 1971)
have led some subsequent investigators to short-cut Heckman's
original definition of LINERs. For instance, it has become customary to
classify emission-line objects solely on the basis of the [N II] /
H ratio
(e.g., Keel 1983b;
Keel et al. 1985;
Phillips et al. 1986;
Véron-Cetty &
Véron 1986).
While this convention
does permit a convenient first-order separation between nuclei photoionized by
stars (small [N II] / H) and
those photoionized by a harder, AGN-like
spectrum (large [N II] / H), it
provides no information on the excitation
level of the AGN-like objects - in other words, one cannot distinguish
LINERs from Seyfert nuclei. There are two additional complications. A
classification scheme that relies on [N II] /
H alone obviously is sensitive
to variations in the abundance of N, which appears to be enhanced in some
galactic nuclei
(Storchi-Bergmann &
Pastoriza 1989,
1990;
Ho, Filippenko, &
Sargent 1996d).
The net effect would be to falsely designate star-forming
nuclei having enhanced N abundance as AGNs. Moreover, the reliability of the
[N II] / H ratio depends
critically on the accuracy of the separation
between the emission and absorption components of the
H line. Although
the ability to model and remove the stellar contribution to the integrated
spectra is an inherent limitation to any method of classification (see
Section 3
and Section 4), it is preferable to use as many
line ratios as possible to
strengthen confidence in the classification assignment.
In the work to be discussed below, I will be using the classification
criteria advocated by
Veilleux & Osterbrock
(1987),
which are motivated in part by the principles of
Baldwin, Phillips, &
Terlevich (1981).
Based on the dereddened line-intensity ratios [O III]
5007 /
H
,
[O I] 6300 /
H, [N II]
6583 /
H, and [S II]
6716, 6731 / H
(H and
H refer only to the narrow
component of the line),
the Veilleux-Osterbrock system is not only relatively insensitive to
extinction corrections, but also conveniently falls within the spectral
range of the optical survey to be described in
Section 4.
For concreteness, the following definitions will be adopted:
H II nuclei ([O I] < 0.08 H, [N
II] < 0.6 H, [S II] < 0.4
H),
Seyferts ([O I] 
0.08 H, [N II] 0.6 H, [S II]
0.4
H, [O III] /
H
3), and LINERs ([O I]
0.17
H, [N II]
0.6
H, [S II]
0.4
H, [O III] /
H < 3). Although the
adopted definition of LINERs differs from that of Heckman, inspection of the
full optical spectra of
Ho, Filippenko, &
Sargent (1993)
reveals
that emission-line nuclei classified as LINERs based on the Veilleux &
Osterbrock diagrams almost invariably also satisfy Heckman's criteria. This
is a consequence of the inverse correlation between [O III] /
H and
[O II] / [O III] in photoionized gas with fairly low excitation ([O III] /
H
3; see Fig. 2 in
Baldwin et al. 1981).
In addition to these three categories of nuclei,
Ho et al. (1993)
identified a
class of ``transition objects'' (in retrospect, a poor choice of terminology)
whose [O I] strengths are intermediate between those of H II nuclei and
LINERs. Although O-star models with an appropriate choice of parameters can
account for their line-intensity ratios of these objects
(Filippenko & Terlevich
1992),
an alternative explanation is that these
objects are composite systems having both an H II region and a LINER component
(Ho et al. 1993).
We will define transition objects using the same criteria as
for LINERs, except that 0.08 H
[O I] < 0.17
H.
It should be emphasized that the classification process is not always
straightforward, since the three conditions involving the low-ionization
lines do not hold simultaneously in all cases. In view of potential selective
N enhancement in galactic nuclei, less weight is given to the [N II] /
H
ratio than to either [O I] / H or
[S II] / H. [O I] /
H, if reliably
determined, deserves the most weight, since it is most sensitive to the shape
of the ionizing spectrum. Figure 1 shows sample
spectra of the various classes of objects outlined above.
|
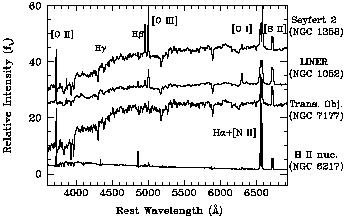
Figure 1. Sample optical spectra of the various classes of emission-line nuclei. |