


1.1 Cumulative Distributions
Very often it is desired to know the probability of finding x between
certain limits, e.g, P(x1  x
x  x2). This is given by the cumulative or
integral distribution
x2). This is given by the cumulative or
integral distribution
where we have assumed P(x) to be continuous. If P(x) is
discrete, the integral is replaced by a sum,
By convention, also, the probability distribution is normalized to 1,
i.e.,
if x is continuous or
if x is discrete. This simply says that the probability of observing
one of the possible outcomes in a given trial is defined as 1. It
follows then that P(xi) or 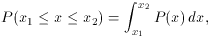
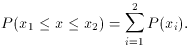
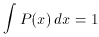
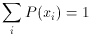
 P(x)dx cannot be greater than 1 or less
than 0.
P(x)dx cannot be greater than 1 or less
than 0.