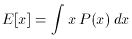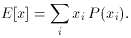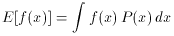1.2 Expectation Values
An important definition which we will make use of later is the expectation value of a random variable or a random variable function. If x is a random variable distributed as P(x), then
is the expected value of x. The integration in (5) is over all
admissible x. This, of course, is just the standard notion of an
average value. For a discrete variable, (5) becomes a sum
Similarly, if f(x) is a function of x, then
is the expected value of f(x).
To simplify matters in the remainder of this section, we will
present results assuming a continuous variable. Unless specified
otherwise, the discrete case is found by replacing integrals with a
summation.