


Example 1. Consider the simple experiment proposed in Sect. 3.2 to measure the length of an object. The following results are from such a measurement:
| 17.62 | 17.62 | 17.615 | 17.62 | 17.61 |
| 17.61 | 17.62 | 17.625 | 17.62 | 17.6 |
| 17.61 | 17.615 | 17.61 | 17.605 | 17.61 |
What is the best estimate for the length of this object?
Since the errors in the measurement are instrumental, the measurements are Gaussian distributed. From (49), the best estimate for the mean value is then
while (52) gives the standard deviation
This can now be used to calculate the standard error of the mean (50),
The best value for the length of the object is thus
Note that the uncertainty on the mean is given by the standard error
of the mean and not the standard deviation!
 = 17.61533
= 17.61533
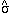 = 5.855 x 10-3.
= 5.855 x 10-3.
 (
( ) =
) = 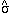 /
/
 15 = 0.0015.
15 = 0.0015.