


5.3 Determination of Count Rates and Their Errors
Example 3. Consider the following series of measurements of the counts per minute from a detector viewing a 22Na source,
| 2201 | 2145 | 2222 | 2160 | 2300 |
What is the decay rate and its uncertainty?
Since radioactive decay is described by a Poisson distribution, we use the estimators for this distribution to find
The count rate is thus
It is interesting to see what would happen if instead of counting
five one-minute periods we had counted the total 5 minutes without
stopping. We would have then observed a total of 11028 counts. This
constitutes a sample of n = 1. The mean count rate for 5 minutes is
thus 11208 and the error on this, 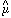 =
=
 = 2205.6 and
= 2205.6 and
 (
(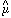 ) =
) =  (
( / n) =
/ n) =  (2205.6 / 5) = 21.
(2205.6 / 5) = 21.
 =
=  11208 = 106. To
find the
counts per minute, we divide by 5 (see the next section) to obtain
2206 ± 21, which is identical to what was found before. Note that the
error taken was the square root of the count rate in 5 minutes. A
common error to be avoided is to first calculate the rate per minute
and then take the square root of this number.
11208 = 106. To
find the
counts per minute, we divide by 5 (see the next section) to obtain
2206 ± 21, which is identical to what was found before. Note that the
error taken was the square root of the count rate in 5 minutes. A
common error to be avoided is to first calculate the rate per minute
and then take the square root of this number.