


5.4 Null Experiments. Setting Confidence Limits When No Counts Are Observed
Many experiments in physics test the validity of certain theoretical conservation laws by searching for the presence of specific reactions or decays forbidden by these laws. In such measurements, an observation is made for a certain amount of time T. Obviously, if one or more events are observed, the theoretical law is disproven. However, if no events are observed, the converse cannot be said to be true. Instead a limit on the life-time of the reaction or decay is set.
Let us assume therefore that the process has some mean reaction rate
 . Then the probability for
observing no counts in a time period T is
. Then the probability for
observing no counts in a time period T is
This, now, can also be interpreted as the probability distribution for
where we have normalized (57) with the extra factor T. This
probability is known as the confidence level for the interval between
0 to
For a given confidence level, the corresponding interval is, in
general, not unique and one can find other intervals which yield the
same integral probability. For example, it might be possible to
integrate (57) from some lower limit
Example 4. A 50 g sample of 82Se is observed for 100 days for
neutrinoless double beta decay, a reaction normally forbidden by
lepton conservation. However, current theories suggest that this might
occur. The apparatus has a detection efficiency of 20%. No events
with the correct signature for this decay are observed. Set an upper
limit on the lifetime for this decay mode.
Choosing a confidence limit of 90%, (59) yields
where we have corrected for the 20% efficiency of the detector. This
limit must now be translated into a lifetime per nucleus. For 50 g,
the total number of nuclei is
which implies a limit on the decay rate per nucleus of
The lifetime is just the inverse of
where we have converted the units to years. Thus, neutrinoless double
beta decay may exist but it is certainly a rare process!
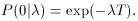
 when no counts are observed in a period T. We can now ask the question:
What is the probability that
when no counts are observed in a period T. We can now ask the question:
What is the probability that  is less
is less  0? From (1),
0? From (1),
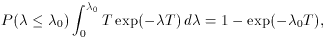
 0. To make a
strong statement we can choose a high confidence
level (CL), for example, 90%. Setting (58) equal to this probability
then gives us the value of
0. To make a
strong statement we can choose a high confidence
level (CL), for example, 90%. Setting (58) equal to this probability
then gives us the value of
 0,
0,

 ' to infinity and still obtain
the same area under the curve. The probability that the true
' to infinity and still obtain
the same area under the curve. The probability that the true
 is
greater than
is
greater than  ' is then
also 90%. As a general rule, however, one
should take those limits which cover the smallest range in
' is then
also 90%. As a general rule, however, one
should take those limits which cover the smallest range in
 .
.


 0 = -1
/ (100 x 0.2) ln (1 - 0.9) = 0.115 day-1,
0 = -1
/ (100 x 0.2) ln (1 - 0.9) = 0.115 day-1,

 0.115 / (3.67 x 1023) = 3.13 x 10-25
day-1.
0.115 / (3.67 x 1023) = 3.13 x 10-25
day-1.
 which yields
which yields

 8.75 x 1021 years 90% CL,
8.75 x 1021 years 90% CL,