


We have seen in the preceding sections how to calculate the errors on directly measured quantities. Very often, however, it is necessary to calculate other quantities from these data. Clearly, the calculated result will then contain an uncertainty which is carried over from the measured data.
To see how the errors are propagated, consider a quantity u = f(x,
y) where x and y are quantities having errors
 x and
x and
 y,
respectively. To simplify the algebra, we only consider a function of
two variables here; however, the extension to more variables will be
obvious. We would like then to calculate the standard deviation
y,
respectively. To simplify the algebra, we only consider a function of
two variables here; however, the extension to more variables will be
obvious. We would like then to calculate the standard deviation
 u as
a function of
u as
a function of  x and
x and
 y. The variance
y. The variance
 u2 can be
defined as
u2 can be
defined as
To first order, the mean
where the partial derivatives are evaluated at the mean values.
Squaring (62) and substituting into (61) then yields
Now taking the expectation value of each term separately and making use
of the definitions (8, 9) and (10), we find
The errors therefore are added quadratically with a modifying term
due to the covariance. Depending on its sign and magnitude, the
covariance can increase or decrease the errors by dramatic amounts. In
general most measurements in physics experiments are independent or
should be arranged so that the covariance will be zero. Equation (64)
then reduces to a simple sum of squares. Where correlations can arise,
however, is when two or more parameters are extracted from the same
set of measured data. While the raw data points are independent, the
parameters will generally be correlated. One common example are
parameters resulting from a fit. The correlations can be calculated in
the fitting procedure and all good computer fitting programs should
supply this information. An example is given in
Section 7.2. If these
parameters are used in a calculation, the correlation must be taken
into account. A second example of this type which might have occurred
to the reader is the estimation of the mean and variance from a set of
data. Fortunately, it can be proved that the estimators (49) and
(52) are statistically independent so that
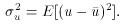
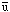 may be
approximated by f(
may be
approximated by f( ,
,
 ). This can be
shown by expanding f(x, y) about
(
). This can be
shown by expanding f(x, y) about
( ,
,
 ) Now, to express the
deviation
of u in terms of the deviations in x and y, let us
expand (u -
) Now, to express the
deviation
of u in terms of the deviations in x and y, let us
expand (u - 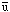 ) to
first order
) to
first order
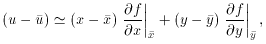
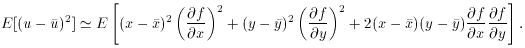
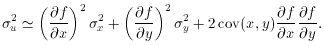
 = 0!
= 0!