


6.1 Examples
As a first example let us derive the formulas for the sum, difference,
product and ratio of two quantities x and y with errors
 x and
x and
 y.
y.
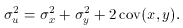
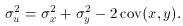
If the covariance is 0, the errors on both a sum and difference then
reduce to the same sum of squares. The relative error,
 u/u, however,
is much larger for the case of a difference since u is smaller. This
illustrates the disadvantage of taking differences between two numbers
with errors. If possible, therefore, a difference should always be
directly measured rather than calculated from two measurements!
u/u, however,
is much larger for the case of a difference since u is smaller. This
illustrates the disadvantage of taking differences between two numbers
with errors. If possible, therefore, a difference should always be
directly measured rather than calculated from two measurements!
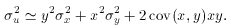
Dividing the left side by u2 and the right side by x2 y2,
Dividing both sides by u2 as in (iii), we find
which, with the exception of the sign of the covariance term is
identical to the formula for a product. Equation (68) is generally
valid when the relative errors are not too large. For ratios of small
numbers, however, (68) is inapplicable and some additional
considerations are required. This is treated in detail by James and
Roos [Ref. 1].
Example 5. The classical method for measuring the polarization of a
particle such as a proton or neutron is to scatter it from a suitable
analyzing target and to measure the asymmetry in the scattered
particle distribution. One can, for example, count the number of
particles scattered to the left of the beam at certain angle and to
the right of the beam at the same corresponding angle. If R is the
number scattered to the right and L the number to the left, the
asymmetry is then given by
Calculate the error on
This is a straight forward application of (64). Taking the
derivatives of
where the total number of counts Ntot = R +
L. The error is thus
The covariance is obviously 0 here since the measurements are
independent. The errors on R and L are now given by the Poisson
distribution, so that
If the asymmetry is small such that R
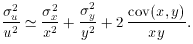
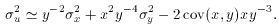
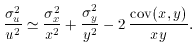
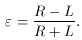
 as
a function of the counts R and L.
as
a function of the counts R and L.
 , we thus find
, we thus find
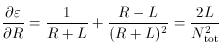
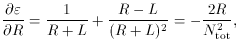
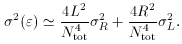
 R2 = R and
R2 = R and
 L2
= L. Substituting into the above, then yields
L2
= L. Substituting into the above, then yields
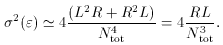
 L
L
 Ntot / 2, we
have the result that
Ntot / 2, we
have the result that