2.3. Standard cosmological solutions
When
k = 
= 0 the Friedmann
and fluid equations can readily
be solved for the equations of state given earlier, leading to the
classic cosmological solutions
In both cases the density falls as t-2. When k
= 0 we have the
freedom to rescale a and it is normally chosen to be unity at the
present, making physical and comoving scales coincide. The
proportionality constants are then fixed by setting the density to be
A more intriguing solution appears for domination by the cosmological
constant, namely
This is equivalent to the solution for a fluid with equation of
state p
More complicated solutions can also be found for mixtures of
components. For example, if there is both matter and radiation the
Friedmann equation can be solved using conformal time
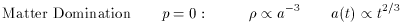
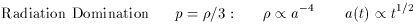
0 at time
t0, where here and throughout the subscript zero
indicates present value.
= -.
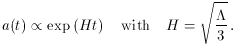
The fluid equation then gives
= 0
and hence
/
8
G.
=
dt /
a, while if there is matter and a non-zero curvature term the
solution can be given either in parametric form using normal time t,
or in closed form with conformal time.