


2.4. Critical density and the density parameter
The critical density
 c is
defined as that giving a
spatially-flat geometry, k = 0, in the absence of a cosmological
constant. From the Friedmann equation, this implies
c is
defined as that giving a
spatially-flat geometry, k = 0, in the absence of a cosmological
constant. From the Friedmann equation, this implies
Densities are often measured as fractions of
The quantity
A similar definition can be employed for the cosmological constant,
giving
and when both density and cosmological constant are present the
condition for spatial flatness is
The present value of the Hubble parameter is still not that well
known, and is parametrized as
where h is normally assumed to lie in the range
0.5 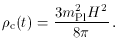
 c :
c :
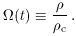
 is known as the
density parameter, and can be
applied to individual types of material as well as the total density.
is known as the
density parameter, and can be
applied to individual types of material as well as the total density.
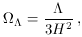
 +
+

 = 1.
= 1.
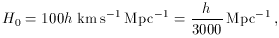
 h
h
 0.8. The present critical density is
0.8. The present critical density is